Zero

Zero jest liczbą całkowitą oznaczaną 0, która używana jako liczba licząca oznacza, że nie ma w niej żadnych obiektów. Jest to jedyna liczba całkowita (a w zasadzie jedyna liczba rzeczywista), która nie jest ani ujemna, ani dodatnia. O liczbie, która nie jest zerem, mówi się, że jest niezerowa. Korzeń funkcji jest również czasami znany jako „a zero of .”

Segment Schoolhouse Rock „My Hero, Zero” wychwala zalety zera takimi pochwałami, jak: „My hero, zero Such a funny little hero But till you came along We counted on our fingers and toes Now you’re here to stay And nobody really knows How wonderful you are Why we could never reach a star Without you, zero, my hero How wonderful you are.”

Zero jest powszechnie uważane za posiadające faktoryzację (np, w poleceniu FactorInteger w języku Wolframa). Z drugiej strony, dzielniki i funkcja dzielnika są na ogół przyjmowane jako niezdefiniowane, ponieważ zgodnie z konwencją, (tj. dzieli 0) dla każdego z wyjątkiem zero.

Ponieważ liczba permutacji elementów 0 wynosi 1, (zero factorial) jest zdefiniowane jako 1 (Wells 1986, s. 31). Definicja ta jest przydatna do wyrażania wielu matematycznych tożsamości w prostej formie.

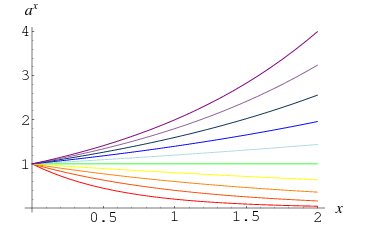
Liczba inna niż 0 podniesiona do potęgi 0 jest zdefiniowana jako 1, co wynika z granicy

Fakt ten ilustruje zbieżność krzywych przy na powyższym wykresie, który pokazuje dla , 0.4, …, 2.0. Można to również zobaczyć bardziej intuicyjnie, zauważając, że wielokrotnie biorąc pierwiastek kwadratowy z liczby daje mniejsze i mniejsze liczby, które zbliżają się do jednego od góry, podczas gdy robi to samo z liczbą między 0 i 1 daje większe i większe liczby, które zbliżają się do jednego od dołu. Dla pierwiastków kwadratowych, całkowita moc wzięta jest , która zbliża się do 0 jak jest duży, dając w granicy, że jest duży.

sam jest niezdefiniowany. Brak dobrze zdefiniowanego znaczenia dla tej wielkości wynika z wzajemnie sprzecznych faktów, że jest zawsze 1, więc powinna być równa 1, ale jest zawsze 0 (dla ), więc powinna być równa 0. Można by argumentować, że jest naturalną definicją, ponieważ

Jednak granica nie istnieje dla ogólnych złożonych wartości . Dlatego wybór definicji dla jest zwykle określany jako nieokreślony.

Zdefiniowanie pozwala jednak na proste wyrażenie niektórych formuł (Knuth 1992; Knuth 1997, s. 57), czego przykładem jest piękny wzór analityczny na całkę uogólnionej funkcji sinc

dany przez Kogana (por. Espinosa i Moll 2000), gdzie , , a jest funkcją podłogi.

Twierdzenie Richardsona jest fundamentalnym wynikiem w teorii rozstrzygalności, który stwierdza, że określenie, czy nawet proste wyrażenia są identycznie równe zeru, jest w zasadzie nierozstrzygalne, a co dopiero w praktyce.

Poniższa tabela podaje kilka liczb pierwszych takich, że rozwinięcie dziesiętne nie zawiera zer dla małych (problem przypominający pytanie Gelfanda). Największą znaną , dla której nie zawiera zer jest 86 (Madachy 1979), przy czym nie ma innych (M. Cook, pers. comm., Sep. 26, 1997 i Mar. 16, 1998), poprawiając granicę uzyskaną przez Beeler i Gosper (1972). Wartości takie, że pozycje najbardziej prawego zera w wzrastają to 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, … (OEIS A031140). Pozycje, na których występują najbardziej prawe zera, to: 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, … (OEIS A031141). Najbardziej prawe zero występuje na 217 miejscu po przecinku, najdalej na potęgach do .

	Sloane	takie, że nie zawiera żadnych 0s
2	A007377	1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, …
3	A030700	1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, …
4	A030701	1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, …
5	A008839	1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, …
6	A030702	1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, …
7	A030703	1, 2, 3, 6, 7, 10, 11, 19, 35
8	A030704	1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24, 27
9	A030705	1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34
11	A030706	1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, …

Chociaż nie zostało udowodnione, że liczby wymienione powyżej są jedynymi bez zer dla danej bazy, prawdopodobieństwo, że istnieją jakiekolwiek dodatkowe jest znikomo małe. Przy tym założeniu, ciąg największych takich, że nie zawiera zer dla , 3, … jest wtedy dany przez 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, … (OEIS A020665).

.