Zero

Zero é o número inteiro denotado 0 que, quando usado como um número de contagem, significa que nenhum objeto está presente. É o único inteiro (e, na verdade, o único número real) que não é nem negativo nem positivo. Um número que não é zero é dito como não zero. Uma raiz de uma função também é por vezes conhecida como “um zero de “

O segmento da Schoolhouse Rock “My Hero, Zero” exalta as virtudes do zero com elogios como, “Meu herói, zero Um heróizinho tão engraçado Mas até tu apareceres Contamos com os dedos dos pés e das mãos Agora estás aqui para ficar E ninguém sabe realmente o quão maravilhoso tu és Porque nunca poderíamos alcançar uma estrela Sem ti, zero, meu herói O quão maravilhoso tu és.”

Zero é comumente tomado para ter a factorização (por exemplo.., no comando FactorInteger da Wolfram Language). Por outro lado, os divisores e função divisora são geralmente tomados para serem indefinidos, já que por convenção, (ou seja, divide 0) para cada exceto zero.

Porque o número de permutações de 0 elementos é 1, (fatorial zero) é definido como 1 (Wells 1986, p. 31). Esta definição é útil para expressar muitas identidades matemáticas de forma simples.

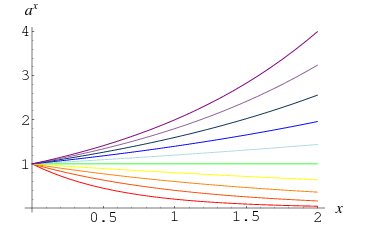
Um número diferente de 0 levado à potência 0 é definido como 1, o que decorre do limite

Este facto é ilustrado pela convergência de curvas em no gráfico acima, que mostra para , 0.4, …, 2.0. Também pode ser visto mais intuitivamente observando que tomando repetidamente a raiz quadrada de um número dá números cada vez menores que se aproximam de um de cima, enquanto que fazendo o mesmo com um número entre 0 e 1 dá números cada vez maiores que se aproximam de um de baixo. Para raízes quadradas, a potência total tomada é , que se aproxima de 0 como é grande, dando no limite que é grande.

em si mesmo é indefinido. A falta de um significado bem definido para esta quantidade decorre dos factos mutuamente contraditórios que é sempre 1, portanto deve ser igual a 1, mas é sempre 0 (para ), portanto deve ser igual a 0. Poder-se-ia argumentar que é uma definição natural já que

No entanto, o limite não existe para valores complexos gerais de . Portanto, a escolha da definição para é geralmente definida para ser indeterminada.

No entanto, definir permite que algumas fórmulas sejam expressas de forma simples (Knuth 1992; Knuth 1997, p. 57), um exemplo da qual é a bela fórmula analítica para a integral da função sinc generalizada

dado por Kogan (cf. Espinosa e Moll 2000), onde , , e é a função do chão.

O teorema de Richardson é um resultado fundamental na teoria da decisão que estabelece que a determinação de se mesmo expressões simples são identicamente iguais a zero é indecidível em princípio, quanto mais na prática.

A tabela seguinte dá os primeiros números tal que a expansão decimal de não contém zeros para pequenos (um problema que se assemelha à questão de Gelfand.) O maior conhecido para o qual não contém zeros é 86 (Madachy 1979), sem outros (M. Cook, pers. comm.., 26 de Setembro de 1997 e 16 de Março de 1998), melhorando o limite obtido por Beeler e Gosper (1972). Os valores de tal forma que as posições do zero mais à direita em aumentos são 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, … (OEIS A031140). As posições em que os zeros mais à direita ocorrem são 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, … (OEIS A031141). O zero mais à direita de ocorre na 217ª casa decimal, o mais distante para potências até .

	Sloane	tal que não contém 0s
2	A007377	1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, …
3	A030700	1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, …
4	A030701	1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, …
5	A008839	1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, …
6	A030702	1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, …
7	A030703	1, 2, 3, 6, 7, 10, 11, 19, 35
8	A030704	1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24, 27
9	A030705	1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34
11	A030706	1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, …

Embora não tenha sido provado que os números listados acima são os únicos sem zeros para uma determinada base, a probabilidade de que existam outros adicionais é muito pequena. Sob esta suposição, a sequência de maiores tal que não contém zeros para , 3, … é então dada por 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, … (OEIS A020665).