Zéro

Le zéro est le nombre entier noté 0 qui, lorsqu’il est utilisé comme un nombre à compter, signifie qu’aucun objet n’est présent. C’est le seul nombre entier (et, en fait, le seul nombre réel) qui n’est ni négatif ni positif. Un nombre qui n’est pas nul est dit non nul. Une racine d’une fonction est aussi parfois appelée « un zéro de . »

Le segment de Schoolhouse Rock « Mon héros, zéro » vante les vertus du zéro avec des éloges tels que : « Mon héros, zéro Un si drôle de petit héros Mais jusqu’à ce que tu arrives Nous comptions sur nos doigts et nos orteils Maintenant tu es là pour rester Et personne ne sait vraiment Combien tu es merveilleux Pourquoi nous ne pourrions jamais atteindre une étoile Sans toi, zéro, mon héros Combien tu es merveilleux. »

Zéro est communément considéré comme ayant la factorisation (par ex, dans la commande FactorInteger du Wolfram Language). D’autre part, les diviseurs et la fonction diviseur sont généralement considérés comme indéfinis, puisque par convention, (c’est-à-dire que divise 0) pour chaque sauf zéro.

Parce que le nombre de permutations des éléments 0 est 1, (factorielle de zéro) est défini comme 1 (Wells 1986, p. 31). Cette définition est utile pour exprimer de nombreuses identités mathématiques sous une forme simple.

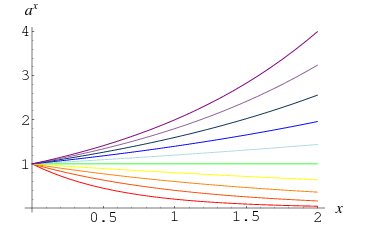
Un nombre autre que 0 pris à la puissance 0 est défini comme étant 1, ce qui découle de la limite

Ce fait est illustré par la convergence des courbes à dans le tracé ci-dessus, qui montre pour , 0.4, …, 2.0. On peut aussi le voir de manière plus intuitive en notant que la prise répétée de la racine carrée d’un nombre donne des nombres de plus en plus petits qui s’approchent de un par le haut, alors que faire la même chose avec un nombre entre 0 et 1 donne des nombres de plus en plus grands qui s’approchent de un par le bas. Pour les racines carrées , la puissance totale prise est , qui se rapproche de 0 lorsque est grand, donnant dans la limite où est grand.

lui-même est indéfini. L’absence d’une signification bien définie pour cette quantité découle des faits mutuellement contradictoires que est toujours 1, donc devrait être égal à 1, mais est toujours 0 (pour ), donc devrait être égal à 0. On pourrait argumenter que est une définition naturelle puisque

Cependant, la limite n’existe pas pour les valeurs complexes générales de . Par conséquent, le choix de la définition de est habituellement défini comme indéterminé.

Cependant, la définition de permet d’exprimer simplement certaines formules (Knuth 1992 ; Knuth 1997, p. 57), dont un exemple est la belle formule analytique de l’intégrale de la fonction sinc généralisée

donnée par Kogan (cf. Espinosa et Moll 2000), où , , et est la fonction plancher.

Le théorème de Richardson est un résultat fondamental de la théorie de la décidabilité qui établit que la détermination de savoir si même des expressions simples sont identiquement égales à zéro est indécidable en principe, et encore moins en pratique.

Le tableau suivant donne les premiers nombres tels que le développement décimal de ne contient pas de zéros pour les petits (un problème qui ressemble à la question de Gelfand.) Le plus grand connu pour lequel ne contient pas de zéros est 86 (Madachy 1979), sans autre (M. Cook, comm. pers, 26 sept. 1997 et 16 mars 1998), améliorant la limite obtenue par Beeler et Gosper (1972). Les valeurs telles que les positions du zéro le plus à droite dans augmentent sont 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, …. (OEIS A031140). Les positions dans lesquelles se trouvent les zéros les plus à droite sont 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, … (OEIS A031141). Le zéro le plus à droite de se trouve à la 217e décimale, la plus éloignée pour les puissances jusqu’à .

	Sloane	tel que ne contient aucun 0
2	A007377	1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, …
3	A030700	1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, …
4	A030701	1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, …
5	A008839	1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, …
6	A030702	1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, …
7	A030703	1, 2, 3, 6, 7, 10, 11, 19, 35
8	A030704	1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24, 27
9	A030705	1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34
11	A030706	1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, …

Bien qu’il n’ait pas été prouvé que les nombres énumérés ci-dessus sont les seuls à ne pas avoir de zéros pour une base donnée, la probabilité qu’il en existe d’autres est infiniment faible. Sous cette hypothèse, la séquence des plus grands tels que ne contient pas de zéros pour , 3, … est alors donnée par 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, …. (OEIS A020665).