Nul

Nul er det hele tal 0, der, når det bruges som et tælletal, betyder, at der ikke er nogen objekter til stede. Det er det eneste hele tal (og faktisk det eneste reelle tal), som hverken er negativt eller positivt. Et tal, der ikke er nul, siges at være ikke-nul. En rod af en funktion er også nogle gange kendt som “et nul af .”

Skolenhouse Rock-afsnittet “My Hero, Zero” ophøjer nulets dyder med lovprisninger som: “My hero, zero Such a funny little hero But till you came along We counted on our fingers and toes Now you’re here to stay And nobody really knows How wonderful you are Why we could never reach a star Without you, zero, my hero How wonderful you are.”

Zero antages almindeligvis at have faktoriseringen (f.eks, i Wolfram Language’s FactorInteger-kommando). På den anden side tages divisorerne og divisorfunktionen generelt for at være udefinerede, da (dvs. dividerer 0) efter konvention for alle undtagen nul.

Da antallet af permutationer af 0-elementer er 1, er (nul-faktorial) defineret som 1 (Wells 1986, s. 31). Denne definition er nyttig til at udtrykke mange matematiske identiteter i enkel form.

Et andet tal end 0 taget til potensen 0 er definerettil at være 1, hvilket følger af grænsen

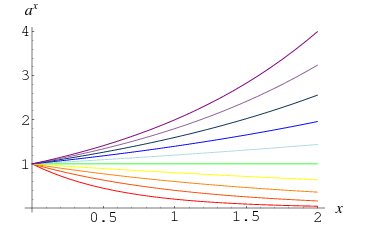
Dette faktum illustreres af konvergensen af kurver ved i ovenstående plot, som viser for , 0.4, …, 2.0. Det kan også ses mere intuitivt ved at bemærke, at gentagne gange at tage kvadratroden af et tal giver mindre og mindre tal, der nærmer sig 1 fra oven, mens det samme med et tal mellem 0 og 1 giver større og større tal, der nærmer sig 1 fra neden. For kvadratrødder er den samlede potens, der tages, , som nærmer sig 0, når er stor, hvilket giver i den grænse, at er stor.

er i sig selv udefineret. Manglen på en veldefineret betydning for denne størrelse følger af de gensidigt modstridende kendsgerninger, at altid er 1, så bør være lig med 1, men er altid 0 (for ), så bør være lig med 0. Man kunne argumentere for, at er en naturlig definition, da

Den grænse eksisterer imidlertid ikke for generelle komplekse værdier af . Derfor defineres valget af definition for normalt som værende ubestemt.

Den definition af gør det imidlertid muligt at udtrykke nogle formler enkelt (Knuth 1992; Knuth 1997, p. 57), et eksempel herpå er den smukke analytiske formel for integralet af den generaliserede sinc-funktion

givet af Kogan (jf. Espinosa og Moll 2000), hvor , , og er gulvfunktionen.

Richardsons sætning er et grundlæggende resultat inden for decidabilitetsteorien, som fastslår, at det er principielt ubeslutsomt at afgøre, om selv simple udtryk er identisk lig nul, for slet ikke at tale om i praksis.

Den følgende tabel angiver de første få tal , således at decimaludvidelsen af ikke indeholder nogen nuller for små (et problem, der ligner Gelfands spørgsmål.) Det største kendte , for hvilket ikke indeholder nogen nuller, er 86 (Madachy 1979), med ingen andre (M. Cook, pers. komm, Sep. 26, 1997 og Mar. 16, 1998), hvilket forbedrer den grænse, der blev opnået af Beeler og Gosper (1972). De værdier , således at positionerne for det yderste højre nul i stiger, er 10, 20, 30, 40, 40, 46, 68, 93, 95, 129, 176, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, … (OEIS A031140). De positioner, hvor de yderste højre nuller forekommer, er 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, … (OEIS A031141). Det yderste nul til højre i forekommer på 217. decimal, det er det yderste for potenser op til .

	Sloane	sådan at ikke indeholder nogen 0’er
2	A007377	1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, …
3	A030700	1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, …
4	A030701	1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, …
5	A008839	1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, …
6	A030702	1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, …
7	A030703	1, 2, 3, 6, 7, 10, 11, 19, 35
8	A030704	1, 2, 3, 5, 6, 6, 8, 8, 9, 11, 12, 13, 17, 24, 27
9	A030705	1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34
11	A030706	1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, …

Selv om det ikke er bevist, at de ovennævnte tal er de eneste uden nuller for en given base, er sandsynligheden for, at der findes yderligere tal, forsvindende lille. Under denne antagelse er sekvensen af de største , således at ikke indeholder nuller for , 3, … givet ved 86, 68, 43, 58, 58, 44, 35, 27, 34, 0, 41, … (OEIS A020665).