Noll

Noll är ett heltal med beteckningen 0 som, när det används som ett räknevärde, betyder att det inte finns några objekt. Det är det enda heltal (och faktiskt det enda verkliga talet) som varken är negativt eller positivt. Ett tal som inte är noll sägs vara icke-noll. En rot i en funktion kallas också ibland för ”en nolla till .”

I Schoolhouse Rock-segmentet ”My Hero, Zero” hyllas nollans förtjänster med sådana lovord som: ”My hero, zero Such a funny little hero But until you came along We counted on our fingers and toes Now you’re here to stay And nobody really knows How wonderful you are Why we could never reach a star Without you, zero, my hero How wonderful you are.”

Noll anses vanligen ha faktoriseringen (t.ex, i Wolframspråkets FactorInteger-kommando). Däremot anses divisorerna och divisorfunktionen i allmänhet vara odefinierade, eftersom (dvs. dividerar 0) enligt konvention för varje utom noll.

Då antalet permutationer av 0-element är 1, är (nollfaktoriell) definierat som 1 (Wells 1986, s. 31). Denna definition är användbar för att uttrycka många matematiska identiteter i enkel form.

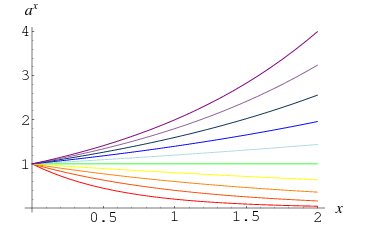
Ett annat tal än 0 som tas till potensen 0 definieras som 1, vilket följer av gränsen

Detta faktum illustreras av konvergensen mellan kurvorna vid i diagrammet ovan, som visar för , 0.4, …, 2.0. Det kan också ses mer intuitivt genom att notera att om man upprepade gånger tar kvadratroten av ett tal får man mindre och mindre tal som närmar sig ett uppifrån, medan om man gör samma sak med ett tal mellan 0 och 1 får man större och större tal som närmar sig ett nedifrån. För kvadratrötter är den totala potensen som tas , som närmar sig 0 när är stor, vilket ger i gränsen att är stor.

är i sig odefinierad. Avsaknaden av en väldefinierad betydelse för denna kvantitet följer av de ömsesidigt motsägelsefulla fakta att alltid är 1, så bör vara lika med 1, men är alltid 0 (för ), så bör vara lika med 0. Man skulle kunna hävda att är en naturlig definition eftersom

Den gränsen existerar dock inte för generella komplexa värden av . Därför definieras valet av definition för vanligen som obestämt.

Däremot gör definitionen av det möjligt att uttrycka vissa formler på ett enkelt sätt (Knuth 1992; Knuth 1997, s. 57), ett exempel på detta är den vackra analytiska formeln för integralen av den generaliserade sinc-funktionen

given av Kogan (jfr Espinosa och Moll 2000), där , och är golvfunktionen.

Richardsons sats är ett grundläggande resultat inom teorin om avgörbarhet som fastställer att fastställandet av om även enkla uttryck är identiskt lika med noll är oavgörbart i princip, för att inte tala om i praktiken.

I följande tabell anges de första fåtalen så att decimalutvidgningen av inte innehåller några nollor för små (ett problem som liknar Gelfands fråga.) Det största kända för vilket inte innehåller några nollor är 86 (Madachy 1979), med inga andra (M. Cook, pers. komm, Sep. 26, 1997 och Mar. 16, 1998), vilket förbättrar den gräns som erhållits av Beeler och Gosper (1972). De värden så att positionerna för den högra nollan i ökar är 10, 20, 30, 40, 40, 46, 68, 93, 95, 129, 176, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, … (OEIS A031140). De positioner där de högra nollorna förekommer är 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, … (OEIS A031141). Den högra nollan i ligger på den 217:e decimalplatsen, den längst bort för potenser upp till .

	Sloane	så att inte innehåller några nollor
2	A007377	1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, …
3	A030700	1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, …
4	A030701	1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, …
5	A008839	1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, …
6	A030702	1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, …
7	A030703	1, 2, 3, 6, 7, 10, 11, 19, 35
8	A030704	1, 2, 3, 5, 6, 6, 8, 9, 11, 12, 13, 17, 24, 27
9	A030705	1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34
11	A030706	1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, …

Och även om det inte har bevisats att ovanstående tal är de enda utan nollor för en given bas, är sannolikheten för att det finns fler nollor försvinnande liten. Under detta antagande är sekvensen av största så att inte innehåller några nollor för , 3, … given av 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, …. (OEIS A020665).