Różne typy sterowników są wykorzystywane do poprawy działania systemów sterowania. W tym rozdziale omówimy podstawowe regulatory, takie jak regulatory proporcjonalne, pochodne i całkujące.
Kontroler proporcjonalny
Kontroler proporcjonalny wytwarza wyjście, które jest proporcjonalne do sygnału błędu.
$$u(t) =K_P e(t) $$
$prawa strzałka u(t)=K_P e(t)$$
Zastosuj transformatę Laplace’a po obu stronach -.
$$U(s)=K_P E(s)$$
$$frac{U(s)}{E(s)}=K_P$$
Więc, funkcja przenoszenia regulatora proporcjonalnego wynosi $K_P$.
Gdzie,
U(s) jest transformatą Laplace’a sygnału wykonawczego u(t)
E(s) jest transformatą Laplace’a sygnału błędu e(t)
KP jest stałą proporcjonalności
Schemat blokowy układu sterowania z ujemnym sprzężeniem zwrotnym w pętli zamkniętej o jedności wraz z regulatorem proporcjonalnym przedstawiono na poniższym rysunku.
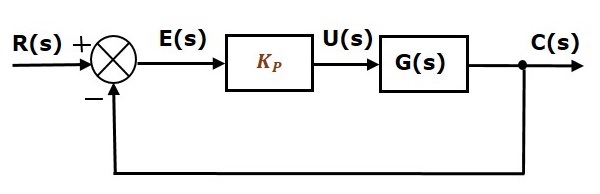
Kontroler proporcjonalny jest używany do zmiany odpowiedzi przejściowej zgodnie z wymaganiami.
Kontroler pochodnej
Kontroler pochodnej wytwarza wyjście, które jest pochodną sygnału błędu.
$$u(t)=K_D \frac{text{d}e(t)}{text{d}t}$$
Zastosuj transformatę Laplace’a po obu stronach.
$$U(s)=K_D sE(s)$$
$$frac{U(s)}{E(s)}=K_D s$$
Więc, funkcja transferu regulatora pochodnej wynosi $K_D s$.
Gdzie, $K_D$ jest stałą pochodnej.
Schemat blokowy układu sterowania z ujemnym sprzężeniem zwrotnym w pętli zamkniętej wraz z regulatorem pochodnej przedstawiono na poniższym rysunku.
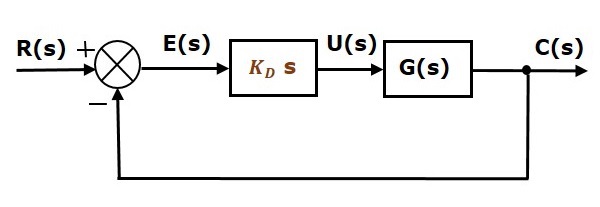
Kontroler pochodnej jest używany do przekształcenia niestabilnego układu sterowania w stabilny.
Kontroler całkujący
Kontroler całkujący wytwarza wyjście, które jest całką sygnału błędu.
$$u(t)=K_I ἀint e(t) dt$$
Zastosuj transformatę Laplace’a po obu stronach –
$U(s)=
$$frac{U(s)}{E(s)}=
Więc, funkcja przenoszenia regulatora całkującego wynosi $$frac{K_I}{s}$.
Gdzie, $K_I$ jest stałą całkową.
Schemat blokowy układu sterowania z zamkniętą pętlą sprzężenia zwrotnego o jedności ujemnej wraz z regulatorem całkującym przedstawiono na poniższym rysunku.
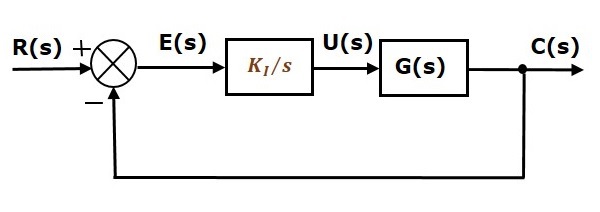
Regulator całkujący służy do zmniejszenia błędu stanu ustalonego.
Przedyskutujmy teraz kombinację podstawowych regulatorów.
Kontroler proporcjonalno-dochodowy (PD)
Kontroler proporcjonalno-dochodowy wytwarza wyjście, które jest kombinacją wyjść kontrolerów proporcjonalnego i pochodnego.
$$u(t)=K_P e(t)+K_D \frac{text{d}e(t)}{text{d}t}$$
Zastosuj transformatę Laplace’a po obu stronach -.
$$U(s)=(K_P+K_D s)E(s)$$
$$frac{U(s)}{E(s)}=K_P+K_D s$$
Więc, funkcja transferu regulatora proporcjonalno-całkująco-pochodnego wynosi $K_P + K_D s$.
Schemat blokowy układu sterowania z zamkniętą pętlą sprzężenia zwrotnego o jedności ujemnej wraz z regulatorem pochodnej proporcjonalnej przedstawiono na poniższym rysunku.
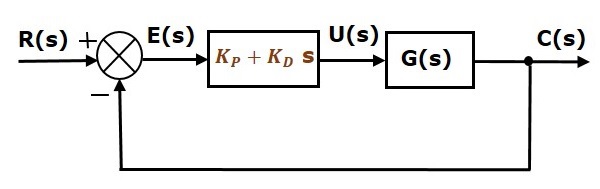
Kontroler pochodnej proporcjonalnej jest używany do poprawy stabilności układu sterowania bez wpływu na błąd stanu ustalonego.
Kontroler proporcjonalno-całkujący (PI)
Kontroler proporcjonalno-całkujący wytwarza wyjście, które jest kombinacją wyjść kontrolerów proporcjonalnego i całkującego.
$$u(t)=K_P e(t)+K_I e(t) dt$$
Zastosuj transformatę Laplace’a po obu stronach -.
$$U(s)=lewa(K_P+frac{K_I}{s} \prawa )E(s)$$
$$frac{U(s)}{E(s)}=K_P+frac{K_I}{s}$$
Więc, funkcja transferu regulatora proporcjonalno-całkującego wynosi $K_P + \frac{K_I} {s}$.
Schemat blokowy układu regulacji z ujemnym sprzężeniem zwrotnym w pętli zamkniętej wraz z regulatorem proporcjonalno-całkującym przedstawiono na poniższym rysunku.
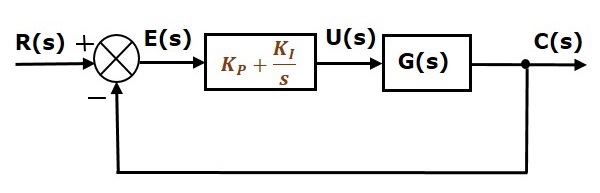
Regulator proporcjonalno-całkujący jest stosowany do zmniejszenia błędu stanu ustalonego bez wpływu na stabilność układu regulacji.
Regulator proporcjonalno-całkująco-pochodny (PID)
Regulator proporcjonalno-całkująco-pochodny wytwarza wyjście, które jest kombinacją wyjść regulatorów proporcjonalnego, całkującego i pochodnego.
$$u(t)=K_P e(t)+K_I całka e(t) dt+K_D \frac{tekst{d}e(t)}{tekst{d}t}$$
Zastosuj transformatę Laplace’a po obu stronach -.
$$U(s)=lewa(K_P+frac{K_I}{s}+K_D s+prawa )E(s)$$
$$frac{U(s)}{E(s)}=K_P+frac{K_I}{s}+K_D s$$
Więc, funkcja transferu regulatora proporcjonalno-całkująco-pochodnego wynosi $K_P + \frac{K_I}{s} + K_D s$.
Schemat blokowy układu sterowania z zamkniętą pętlą sprzężenia zwrotnego o jedności ujemnej wraz z regulatorem pochodnej proporcjonalnej całki przedstawiono na poniższym rysunku.
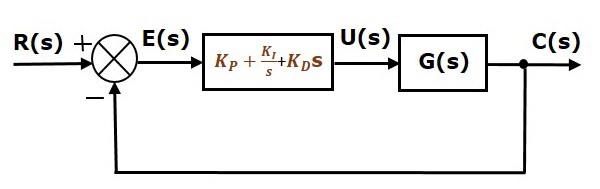
Regulator pochodnej proporcjonalnej całki stosuje się w celu poprawy stabilności układu sterowania oraz zmniejszenia błędu stanu ustalonego.
.