Zacznijmy od zbadania dzielenia wartości z wykładnikami.
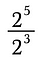
Przypomnijmy, że wykładniki reprezentują wielokrotne mnożenie. Możemy więc zapisać powyższe wyrażenie jako:
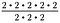
Ponieważ 2/2 = 1, anuluj trzy zbiory 2/2. Pozostaje 2 – 2, czyli 2 podniesione do kwadratu.
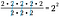
Oczywiście możemy pójść na skróty i odjąć liczbę 2 na dole od liczby 2 na górze. Ponieważ te wielkości są reprezentowane przez ich odpowiednie wykładniki, wszystko co musimy zrobić, to napisać wspólną podstawę z różnicą wartości wykładników jako potęgę.
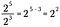
Jeśli uogólnimy tę regułę, mamy następujące, gdzie n reprezentuje niezerową liczbę rzeczywistą, a x i y są również liczbami rzeczywistymi.
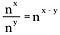
Exploring the Zero Power
Z tego miejsca łatwo wyprowadzić wyjaśnienie, dlaczego każda niezerowa liczba podniesiona do potęgi zerowej równa się 1. Ponownie, spójrzmy na konkretny przykład.
Wiemy, że każda niezerowa liczba podzielona przez siebie równa się 1. Mogę więc napisać, co następuje:
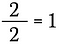
To jest to samo, co napisanie:
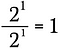
Teraz wykorzystam regułę wykładników z góry, aby przepisać lewą stronę tego równania.
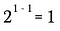
Oczywiście jest to równoważne:
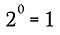
Możemy użyć tego samego procesu, co w tym przykładzie, wraz z powyższą uogólnioną regułą, aby pokazać, że każda niezerowa liczba rzeczywista podniesiona do potęgi zerowej musi dać w wyniku 1.
A co z zerem do potęgi zerowej?
Tutaj sprawy się komplikują. Powyższa metoda łamie się, ponieważ, oczywiście, dzielenie przez zero jest nie-nie. Sprawdźmy dlaczego.
Zaczniemy od przyjrzenia się częstemu błędowi dzielenia przez zero.
Jak to jest z 2÷0? Przyjrzyjmy się, dlaczego nie możemy tego zrobić.
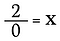
Dzielenie jest tak naprawdę tylko formą mnożenia, więc co się stanie, jeśli przepiszę powyższe równanie jako:
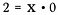
Jaka wartość mogłaby spełnić to równanie dla x?
Nie ma żadnej wartości! Każda liczba pomnożona przez zero daje w wyniku zero, nigdy nie może być równa 2. Dlatego mówimy, że dzielenie przez zero jest nieokreślone. Nie ma możliwego rozwiązania.
Teraz spójrzmy na 0÷0.
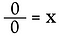
Ponownie, przepiszmy to jako problem z mnożeniem.
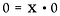
Tutaj mamy do czynienia z zupełnie inną sytuacją. Rozwiązaniem dla x może być KAŻDA liczba rzeczywista! Nie ma sposobu, aby określić, czym jest x. Stąd, 0/0 jest uważane za nieokreślone*, a nie nieokreślone.
Jeśli spróbujemy użyć powyższej metody z zerem jako bazą do określenia, czym byłoby zero do potęgi zerowej, natychmiast się zatrzymamy i nie możemy kontynuować, ponieważ wiemy, że 0÷0 ≠ 1, ale jest nieokreślone.
Więc czym jest równe zero do potęgi zerowej?
To jest wysoce dyskusyjne. Niektórzy uważają, że powinno być zdefiniowane jako 1, podczas gdy inni uważają, że jest to 0, a niektórzy uważają, że jest to nieokreślone. Istnieją dobre argumenty matematyczne dla każdego z nich, i być może jest to najbardziej poprawnie uważane za nieokreślone.
Mimo to, społeczność matematyczna jest za definiowaniem zera do potęgi zerowej jako 1, przynajmniej dla większości celów.
Może pomocna definicja wykładników dla matematyka amatora jest następująca:
.