Kąt utworzony, gdy promień
jest owinięty wokół okręgu:
 |
1 Radian ma około 57,2958 stopnia. |
Dlaczego „57,2958…” stopni? Zobaczymy za chwilę.
Radian jest czystą miarą opartą na promieniu okręgu:
Radian: kąt utworzony, gdy weźmiemy promień
i owiniemy go wokół okręgu.
Radiany i stopnie
Zobaczmy dlaczego 1 radian jest równy 57.2958… stopniom:
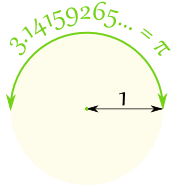
W półokręgu jestπ radianów, czyli również 180°
Aby przejść od radianów do stopni: pomnóż przez 180, podziel przez π
Aby przejść od stopni do radianów: pomnóż przez π, podziel przez 180
Tutaj jest tabela wartości równoważnych:
| Stopnie | Radiany (exact) |
Radiany (approx) |
|---|---|---|
| 30° | π/6 | 0.524 |
| 45° | π/4 | 0.785 |
| 60° | π/3 | 1.047 |
| 90° | π/2 | 1.571 |
| 180° | π | 3.142 |
| 270° | 3π/2 | 4,712 |
| 360° | 2π | 6,283 |
Przykład: Ile radianów w pełnym okręgu?
Wyobraź sobie, że wycinasz kawałki sznurka o długości dokładnie od środka do obwodu koła …
… ile kawałków potrzebujesz, aby raz okrążyć okrąg?
Odpowiedź: 2π (lub około 6,283 kawałków sznurka).
Radiany preferowane przez matematyków
Ponieważ radian jest oparty na czystej idei „promienia ułożonego wzdłuż obwodu”, często daje proste i naturalne wyniki, gdy jest używany w matematyce.
Na przykład, spójrz na funkcję sinus dla bardzo małych wartości:

