Modelowanie matematyczne

by admin Leave Comment

Cele nauczania

  • Wprowadzenie do funkcji kwadratowych
    • Zdefiniuj funkcję kwadratową
    • Oceń funkcję kwadratową funkcji
    • Ocena funkcji akordowej
    • Zapisanie funkcji akordowej w danym zastosowaniu
  • Graph Funkcje akordowe
    • Dane funkcji akordowej
      • Dane funkcji akordowejzdefiniowaną funkcję, naszkicuj wykres
      • Zapisz dziedzinę i zakres funkcji fragmentarycznej na podstawie jej wykresu

Niektóre funkcje występują w kawałkach. W tym rozdziale dowiemy się, jak zdefiniować i wykresać funkcje, które są zasadniczo zbiorem dyskretnych kawałków. Przykłady czegoś zdefiniowanego w ten sposób obejmują projektowanie profilu samochodu, ustalanie planu telefonii komórkowej i obliczanie stawek podatku dochodowego. Na przykład, stawka podatkowa zależy od dochodu i jest taka sama dla pewnego zakresu dochodów, jak pokazano w poniższej tabeli:

Marginalna stawka podatkowa Dochód podlegający opodatkowaniu dla singla Dochód podlegający opodatkowaniu dla małżeństwa lub wdowy (wdowca) Income Married Filing Separately Taxable Income Head of Household Taxable Income
10% $0 – $9,275 $0 – $18,550 $0 – $9,275 $0 – $13,250
15% $9,276 – $37,650 $18,551 – $75,300 $9,276 – $37,650 $13,251 – $50,400
25% $37,651 – $91,150 $75,301 – $151,900 $37,651 – $75,950 $50,401 – $130,150
28% $91,151 – $190,150 $151,901 – $231,450 $75,951 – $115,725 $130,151 – $210,800
33% $190,151 – $413,350 $231,451 – $413,350 $115,726 – $206,675 $210,801 – $413,350
35% $413,351 – $415,050 $413,351 – $466,950 $206,676 – $233,475 $413,351 – $441,000
39.6% $415,051+ $466,951+ $233,476+ $441,001+

Funkcja fragmentaryczna to funkcja, w której do określenia danych wyjściowych na różnych fragmentach dziedziny używa się więcej niż jednego wzoru.

Używamy funkcji fragmentarycznych do opisania sytuacji, w których reguła lub relacja zmienia się, gdy wartość wejściowa przekracza pewne „granice”. Na przykład, często spotykamy się z sytuacjami w biznesie, dla których koszt za sztukę pewnego przedmiotu jest obniżany, gdy liczba zamówionych sztuk przekroczy pewną wartość. Nawiasy podatkowe są kolejnym przykładem funkcji akordowych w świecie rzeczywistym. Na przykład, rozważmy prosty system podatkowy, w którym dochody do $10,000 są opodatkowane w wysokości 10%, a każdy dodatkowy dochód jest opodatkowany w wysokości 20%. Podatek od całkowitego dochodu, S, wynosiłby 0,1S, jeśli S wynosi $10,000 i 1000 + 0,2 (S – $10,000), jeśli S> $10,000.

Piecewise Function

A piecewise function is a function in which more than one formula is used to define the output. Każda formuła ma swoją własną dziedzinę, a dziedziną funkcji jest unia wszystkich tych mniejszych dziedzin. Ideę tę zapisujemy w następujący sposób:

fleft(xright)=begin{cases}text{formuła 1 jeśli x jest w dziedzinie 1}text{formuła 2 jeśli x jest w dziedzinie 2}text{formuła 3 jeśli x jest w dziedzinie 3}end{cases}

W notacji akordowej, funkcja wartości bezwzględnej ma postać

|x|=

Evaluate a Piecewise Defined Function

W pierwszym przykładzie pokażemy jak ocenić funkcję zdefiniowaną akordowo. Zauważ, jak ważne jest, aby zwrócić uwagę na domenę, aby określić, które wyrażenie użyć do oceny danych wejściowych.

Przykład

Podając funkcję

f(x)={begin{cases}7x+3}tekst{ if }x<0}7x+6}tekst{ if }x{ge{0}}end{cases},

oceniaj:

  1. f (-1)
  2. f (0)
  3. f (2)
Pokaż odpowiedź

1.f(x) jest zdefiniowana jako 7x+3 dla x=-1, ponieważ }-1<0.

Oceń: f(-1)=7(-1)+3=-7+3=-4

2. f(x) jest zdefiniowana jako 7x+6 dla x=0

Oceń: f(0)=7(0)+6=0+6=6

3. f(x) jest zdefiniowana jako 7x+6 dla x=2

4.

Oszacuj: f(2)=7(2)+6=14+6=20

W poniższym filmie pokazujemy jak oszacować kilka wartości biorąc pod uwagę funkcję zdefiniowaną fragmentarycznie.

W następnym przykładzie pokazujemy, jak ocenić funkcję, która modeluje koszt transferu danych dla firmy telefonicznej.

Przykład

Firma telefonii komórkowej używa poniższej funkcji do określenia kosztu, C, w dolarach za g gigabajtów transferu danych.

Cleft(gright)=begin{cases}{25}text{ if }{ 0 }<{ g }<{ 2 } 10g+5}text{ if }{ g}ge{ 2 }}end{cases}

Znajdź koszt użycia 1.5 gigabajtów danych oraz koszt użycia 4 gigabajtów danych.

Show Answer

Aby znaleźć koszt użycia 1,5 gigabajta danych, C(1,5), sprawdzamy najpierw, w której części dziedziny znajduje się nasze dane wejściowe. Ponieważ 1,5 jest mniejsze od 2, korzystamy z pierwszego wzoru.

C(1,5) = 25$

Aby znaleźć koszt użycia 4 gigabajtów danych, C(4), widzimy, że nasz wkład 4 jest większy od 2, więc korzystamy z drugiego wzoru.

C(4)=10(4)+5=45

Analiza rozwiązania

Funkcja jest przedstawiona na poniższym wykresie. Widzimy, gdzie funkcja przechodzi od stałej do linii o dodatnim nachyleniu przy g=2. Wykresy dla różnych wzorów nanosimy na wspólny zestaw osi, upewniając się, że każdy wzór jest stosowany w odpowiedniej dziedzinie.

C(g) = Cleft(g)=begin{cases}{25}}text{ if }{ 0 }<{ g }<{ 2 } } 10g+5}text{ if }{ g}ge{ 2 }}end{cases}

. Napisz funkcję zdefiniowaną fragmentarycznie

W ostatnim przykładzie pokażemy, jak napisać funkcję zdefiniowaną fragmentarycznie, która modeluje cenę wycieczki do muzeum z przewodnikiem.

Przykład

Muzeum pobiera 5$ od osoby za zwiedzanie z przewodnikiem w grupie od 1 do 9 osób lub stałą opłatę 50$ za grupę 10 lub więcej osób. Napisz funkcję związaną z liczbą osób, n, i kosztem, C.

Show Answer

Potrzebne będą dwa różne wzory. Dla wartości n poniżej 10, C=5n. Dla wartości n, które są równe 10 lub większe, C=50.

C(n)=begin{cases}{5n} tekst{ if }{0}<{n}<{10} tekst{ if }{n} tekst{cases} 10}end{cases}

Analiza rozwiązania

Funkcja jest przedstawiona na rysunku 21. Wykres jest linią ukośną od n=0 do n=10, a następnie stałą. W tym przykładzie dwa wzory zgadzają się w punkcie spotkania, w którym n=10, ale nie wszystkie funkcje akordowe mają tę własność.

W poniższym filmie pokazujemy przykład pisania funkcji zdefiniowanej akordowo, biorąc pod uwagę scenariusz.

Dając funkcję akordową, napisz jej wzór i określ dziedzinę dla każdego przedziału.

  1. Zidentyfikuj przedziały, dla których obowiązują różne reguły.
  2. Zdefiniuj formuły opisujące sposób obliczania danych wyjściowych na podstawie danych wejściowych w każdym przedziale.
  3. Użyj nawiasów klamrowych i wyrażeń if do napisania funkcji.

Wykresy funkcji akordowych

W tym rozdziale wykreślimy funkcje akordowe. Funkcja wykreślona poniżej reprezentuje koszt transferu danych dla danej firmy telefonii komórkowej. Możemy zobaczyć, gdzie funkcja zmienia się ze stałej w linię o dodatnim nachyleniu przy g=2. Kiedy wykreślamy funkcje akordowe, ważne jest, aby upewnić się, że każda formuła jest stosowana w odpowiedniej dziedzinie.Cleft(g)=begin{cases}{25} \text{ if }{ 0 }<{ g }<{ 2 } \10g+5 \text{ if }{ g}ge{ 2 } \end{cases}

W tym przypadku wyjściem jest 25 dla każdej wartości wejściowej z przedziału od 0 do 2. Dla wartości równych lub większych od 2 dane wyjściowe są zdefiniowane jako 10g+5.

Podając funkcję kaskadową, naszkicuj jej wykres.

  1. Wskaż na osi x granice wyznaczone przez przedziały na każdym fragmencie dziedziny.
  2. Dla każdego fragmentu dziedziny wykonaj wykres na tym przedziale, używając odpowiedniego równania odnoszącego się do tego fragmentu. Nie sporządzaj wykresu dwóch funkcji na jednym przedziale, ponieważ naruszałoby to kryteria funkcji.

Przykład

Zarysuj wykres funkcji.

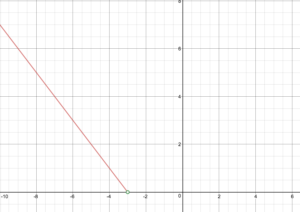
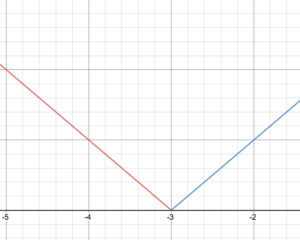
Podając definicję fragmentaryczną f(x)=begin{cases}-x – 3{ if }x < -3{cases} x + 3{ if } x ge -3 end{cases}
Narysuj wykres funkcji f.
Podaj dziedzinę i zakres funkcji.

Show Answer

Początkowo wykonaj wykres linii f(x) = -x-3, wymazując część, w której x jest większe od -3. Umieść otwarty okrąg w punkcie (-3,0).

Następnie umieść na wykresie prostą f(x) = x+3, zaczynając od punktu (-3,0). Zauważ, że dla tej części wykresu punkt (-3,0) jest zawarty, więc możesz usunąć otwarty okrąg.

Dwa wykresy spotykają się w punkcie (-3,0)

Działką tej funkcji są wszystkie liczby rzeczywiste, ponieważ (-3,0)nie jest zawarty jako punkt końcowy dla f(x) = -x-3, ale jest zawarty jako punkt końcowy dla f(x) = x+3.

Przedział tej funkcji zaczyna się od f(x)=0 i zawiera 0, i zmierza do nieskończoności, więc zapisalibyśmy to jako x

W następnym przykładzie wykreślimy funkcję zdefiniowaną w sposób fragmentaryczny, która modeluje koszt wysyłki dla internetowego sprzedawcy komiksów.

Przykład

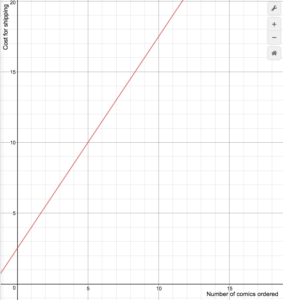
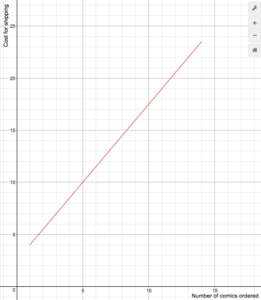
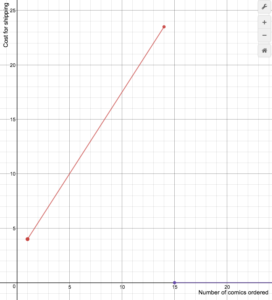
Internetowy sprzedawca komiksów nalicza koszty wysyłki zgodnie z następującym wzorem

S(n)=begin{cases}1,5n+2.5\text{ if }1\le{n}

Narysuj wykres funkcji kosztów.

Show Answer

Na początku narysuj linię S(n)=1,5n+2,5. Możemy skorzystać z przekształceń: jest to pionowe rozciągnięcie tożsamości o współczynnik 1,5, oraz pionowe przesunięcie o 2,5.

S(n)=1,5n+2.5

Teraz możemy wyeliminować fragmenty wykresu, które nie należą do dziedziny na podstawie 1

S(n) = 1.5n+2.5 dla 1<=n<=14

Na koniec dodajemy funkcję stałą S(n)=0 dla danych wejściowych większych lub równych 15. Umieść zamknięte kropki na końcach wykresu, aby zaznaczyć włączenie punktów końcowych.

W poniższym filmie pokazujemy, jak wykreślić wykres funkcji zdefiniowanej fragmentarycznie, która jest liniowa w obu dziedzinach.

Podsumowanie

  • Funkcja fragmentaryczna to funkcja, w której więcej niż jeden wzór jest używany do zdefiniowania wyjścia na różnych fragmentach dziedziny.
  • Ocenianie funkcji fragmentarycznej oznacza, że musisz zwracać baczną uwagę na poprawne wyrażenie użyte dla danego wejścia

Aby wykreślić funkcje fragmentaryczne, najpierw zidentyfikuj, gdzie dziedzina jest podzielona. Wykresy funkcji w dziedzinie przy użyciu narzędzi, takich jak wykreślanie punktów lub przekształcenia. Uważaj, aby używać otwartych lub zamkniętych okręgów na punktach końcowych każdej dziedziny w zależności od tego, czy punkt końcowy jest zawarty.

Dodaj komentarz

Twój adres e-mail nie zostanie opublikowany.