Half Adder i Full Adder Circuit
Half Adder i pełne Adder obwody jest wyjaśnione z ich tabel prawdy w tym artykule. Projekt Full Adder przy użyciu obwodu Half Adder jest również pokazany. Pokazany jest również obwód jednobitowego pełnego addera i wielobitowego dodawania przy użyciu pełnego addera.
Przed przejściem do tego tematu, bardzo ważne jest, aby wiedzieć o logice boolowskiej i bramkach logicznych.
TAKE A LOOK : BOOLEAN LOGIC
TAKE A LOOK : LOGIC GATES
TAKE A LOOK : FLIP FLOPS
What is an Adder?
An adder is a kind of calculator that is used to add two binary numbers. Kiedy mówię kalkulator, nie mam na myśli takiego z przyciskami, ten jest obwodem, który może być zintegrowany z wieloma innymi obwodami dla szerokiej gamy zastosowań. Istnieją dwa rodzaje adderów;
- Half adder
- Full adder
Half Adder
Z pomocą half adder, możemy zaprojektować obwody, które są w stanie wykonać proste dodawanie z pomocą bramek logicznych.
Przyjrzyjmy się najpierw dodawaniu pojedynczych bitów.
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
To są najmniejsze możliwe kombinacje pojedynczych bitów. Ale wynik dla 1+1 to 10. Chociaż ten problem może być rozwiązany za pomocą bramki EXOR, jeśli zależy nam na wyjściu, wynik sumy musi być zapisany jako wyjście 2-bitowe.
Więc powyższe równania mogą być zapisane jako
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
Tutaj wyjście '1’z ’10’ staje się przeniesieniem. Wynik jest pokazany w tabeli prawdy poniżej. 'SUM’ jest normalnym wyjściem, a 'CARRY’ jest przeniesieniem.
INPUTS OUTPUTS
A B SUM CARRY
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
Z równania, widać, że ten 1-bitowy sumator może być łatwo zaimplementowany z pomocą bramki EXOR dla wyjścia 'SUM’ i bramki AND dla przeniesienia. Przyjrzyj się poniższej implementacji.
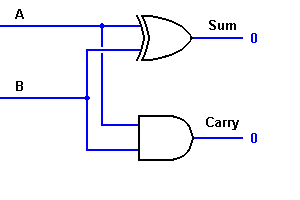
W przypadku złożonego dodawania mogą wystąpić przypadki, gdy trzeba dodać dwa 8-bitowe bajty razem. Można to zrobić tylko z pomocą logiki full-adder.
Full Adder
Ten typ addera jest nieco trudniejszy do zaimplementowania niż half-adder. Główną różnicą między półdrukiem a pełnym drabinką jest to, że pełny drabinka ma trzy wejścia i dwa wyjścia. Pierwsze dwa wejścia to A i B, a trzecie wejście to wejście carry oznaczone jako CIN. Po zaprojektowaniu pełnego sumatora logicznego będziemy mogli połączyć osiem takich sumatorów, aby utworzyć sumator o szerokości bajtu i kaskadować bit przeniesienia z jednego sumatora do drugiego.
Wyjście przeniesienia jest oznaczane jako COUT, a normalne wyjście jest oznaczane jako S. Spójrz na tabelę prawdy.
WEJŚCIA WYJŚCIA
A B CIN COUT S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
Z powyższej tabeli prawda-tabela, można zaimplementować logikę pełnego addera. Widzimy, że wyjście S jest EXOR-em pomiędzy wejściem A a wyjściem półdruku SUM z wejściami B i CIN. Musimy również zauważyć, że COUT będzie prawdziwe tylko wtedy, gdy dowolne z dwóch wejść z trzech są HIGH.
Tak więc, możemy zaimplementować pełny obwód adder z pomocą dwóch obwodów half adder. Pierwszy będzie pół adder będzie używany do dodawania A i B do produkcji częściowej Suma. Druga logika półsumatora może być użyta do dodania CIN do sumy wyprodukowanej przez pierwszy półsumator, aby uzyskać ostateczne wyjście S. Jeśli któraś z logik półsumatora wytworzy przeniesienie, na wyjściu będzie przeniesienie. Tak więc COUT będzie funkcją OR wyjść Carry póładdera. Spójrz na implementację obwodu pełnego dodawania pokazaną poniżej.
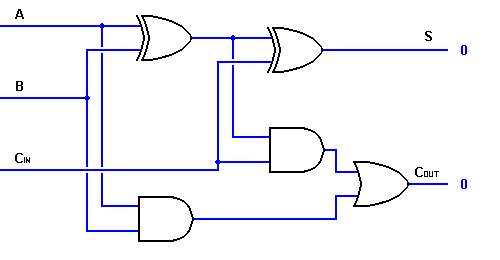
Chociaż implementacja większych schematów logicznych jest możliwa z powyższą logiką pełnego dodawania, do reprezentacji operacji używa się przeważnie prostszego symbolu. Poniżej przedstawiono prostszy schemat jednobitowego pełnego dodawania.
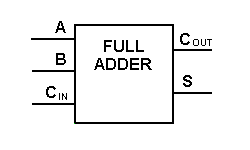
Za pomocą tego typu symbolu możemy dodać dwa bity razem, pobierając przeniesienie z następnego niższego rzędu wielkości i wysyłając przeniesienie do następnego wyższego rzędu wielkości. W komputerze, dla operacji wielobitowej, każdy bit musi być reprezentowany przez pełny adder i musi być dodawany jednocześnie. Tak więc, aby dodać dwie liczby 8-bitowe, potrzeba 8 pełnych sumatorów, które można utworzyć poprzez kaskadowe połączenie dwóch bloków 4-bitowych. Dodawanie dwóch liczb 4-bitowych pokazane jest poniżej.
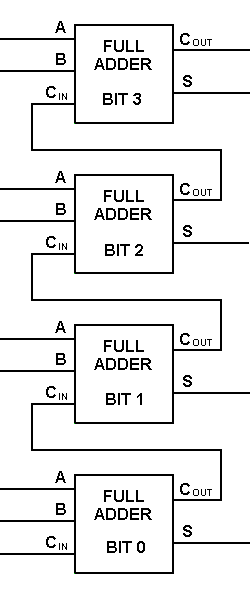
.