Wstęp – Miary odległości w Data Mining
W Data Mining, miara podobieństwa odnosi się do odległości z wymiarami reprezentującymi cechy obiektu danych, w zbiorze danych. Jeśli ta odległość jest mniejsza, będzie wysoki stopień podobieństwa, ale gdy odległość jest duża, będzie niski stopień podobieństwa.
Niektóre z popularnych miar podobieństwa są –
- Euclidean Distance.
- Dystans Manhattan.
- Podobieństwo Jaccard.
- Dystans Minkowski.
- Podobieństwo cosinusoidalne.
Podobieństwo cosinusoidalne jest metryką, pomocną w określaniu, jak bardzo podobne są obiekty danych niezależnie od ich wielkości. Możemy zmierzyć podobieństwo pomiędzy dwoma zdaniami w Pythonie używając podobieństwa cosinusowego. W podobieństwie cosinusowym, obiekty danych w zbiorze danych są traktowane jako wektor. Wzór na znalezienie podobieństwa cosinusowego między dwoma wektorami to –
Cos(x, y) = x . y / ||x|| * ||y||
gdzie,
- x . y = iloczyn (kropka) wektorów „x” i „y”.
- ||x|| i ||y|| = długości dwóch wektorów 'x’ i 'y’.
- ||x| * ||y|| = iloczyn krzyżowy dwóch wektorów 'x’ i 'y’.
Przykład :
Rozważmy przykład na znalezienie podobieństwa między dwoma wektorami – 'x’ i 'y’, za pomocą podobieństwa cosinusowego.
Wektor 'x’ ma wartości, x = { 3, 2, 0, 5 }
Wektor 'y’ ma wartości, y = { 1, 0, 0, 0 }
Wzór na obliczenie podobieństwa cosinusowego to : Cos(x, y) = x . y / ||x|| * ||y||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1∴ Cos(x, y) = 3 / (6.16 * 1) = 0.49
Podobieństwo między dwoma wektorami 'x’ i 'y’ jest dane przez –
∴ Dis(x, y) = 1 - Cos(x, y) = 1 - 0.49 = 0.51
- Podobieństwo cosinusowe między dwoma wektorami jest mierzone w 'θ’.
- Jeśli θ = 0°, wektory „x” i „y” pokrywają się, co dowodzi, że są podobne.
- Jeśli θ = 90°, wektory „x” i „y” są niepodobne.
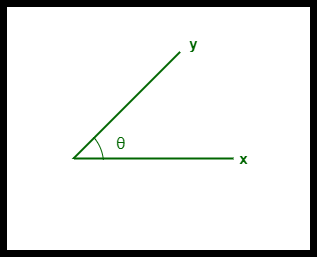
Podobieństwo cosinusoidalne między dwoma wektorami
Zalety :
- Podobieństwo cosinusoidalne jest korzystne, ponieważ nawet jeśli dwa podobne obiekty danych są oddalone od siebie o odległość euklidesową ze względu na rozmiar, nadal mogą mieć mniejszy kąt między sobą. Mniejszy kąt, wyższe podobieństwo.
- Po wykreśleniu na wielowymiarowej przestrzeni, podobieństwo cosinusowe wychwytuje orientację (kąt) obiektów danych, a nie wielkość.