- CELE NAUCZANIA
- Przykład 1. Obliczanie energii uwolnionej w wyniku rozszczepienia
- Strategia
- Rozwiązanie
- Dyskusja
- Przykład 2. Obliczanie energii z kilograma paliwa rozszczepialnego
- Strategia
- Rozwiązanie
- Dyskusja
- PhET Explorations: Nuclear Fission
- Podsumowanie sekcji
- Pytania pojęciowe
- Problemy &Ćwiczenia
- Słowniczek
- Wybrane rozwiązania problemów & Ćwiczenia
CELE NAUCZANIA
Do końca tego rozdziału, będziesz w stanie:
- Zdefiniować rozszczepienie jądrowe.
- Przedstawić reakcję paliwa rozszczepialnego i opisać, co z niej powstaje.
- Opisać kontrolowane i niekontrolowane reakcje łańcuchowe.
Rozszczepienie jądra atomowego to reakcja, w której jądro zostaje rozszczepione (lub pęknięte). Kontrolowane rozszczepienie jest rzeczywistością, natomiast kontrolowana fuzja jądrowa jest nadzieją na przyszłość. Setki elektrowni jądrowych na całym świecie świadczą o tym, że rozszczepienie kontrolowane jest praktyczne i, przynajmniej w krótkim okresie, ekonomiczne, co widać na rysunku 1. Podczas gdy przez dziesiątki lat po katastrofach w TMI i Czarnobylu (a obecnie w Fukushimie Daiichi) energetyka jądrowa cieszyła się niewielkim zainteresowaniem, rosnące obawy związane z globalnym ociepleniem sprawiły, że ponownie zaczęto ją traktować jako realną alternatywę energetyczną. Do końca 2009 roku w 30 krajach działały 442 reaktory, które dostarczały 15% światowej energii elektrycznej. Francja dostarcza ponad 75% energii elektrycznej z energii jądrowej, podczas gdy w USA działają 104 reaktory dostarczające 20% energii elektrycznej. Australia i Nowa Zelandia nie mają żadnego. Chiny budują elektrownie jądrowe w tempie jednego uruchomienia na miesiąc.

Rysunek 1. Ludzie mieszkający w pobliżu tej elektrowni jądrowej nie mają mierzalnego narażenia na promieniowanie, które można by przypisać tej elektrowni. Około 16% światowej energii elektrycznej jest wytwarzane w takich elektrowniach w wyniku kontrolowanego rozszczepienia jądra atomowego. Wieże chłodnicze są najbardziej widocznymi elementami, ale nie są charakterystyczne dla energetyki jądrowej. Reaktor znajduje się w małym kopulastym budynku na lewo od wież. (kredyt: Kalmthouts)
Rozszczepienie jest przeciwieństwem syntezy jądrowej i uwalnia energię tylko wtedy, gdy ciężkie jądra zostają rozszczepione. Jak wspomniano w rozdziale Fuzja jądrowa, energia jest uwalniana, jeżeli produkty reakcji jądrowej mają większą energię wiązania na nukleon (BE/A) niż jądra macierzyste. Rysunek 2 pokazuje, że BE/A jest większe dla jąder o średniej masie niż dla jąder ciężkich, co sugeruje, że gdy ciężkie jądro jest rozszczepiane, produkty mają mniejszą masę na nukleon, a więc masa jest niszczona i w reakcji uwalniana jest energia. Ilość energii przypadająca na reakcję rozszczepienia może być duża, nawet jak na standardy jądrowe. Wykres na rysunku 2 pokazuje, że BE/A wynosi około 7,6 MeV/nukleon dla najcięższych jąder (A około 240), podczas gdy BE/A wynosi około 8,6 MeV/nukleon dla jąder o A około 120. Jeśli więc ciężkie jądro rozpadnie się na pół, to uwolnione zostanie około 1 MeV na nukleon, czyli około 240 MeV na rozszczepienie. Jest to około 10 razy więcej energii niż w przypadku reakcji syntezy jądrowej i około 100 razy więcej niż energia przeciętnego rozpadu α, β lub γ.
Przykład 1. Obliczanie energii uwolnionej w wyniku rozszczepienia
Oblicz energię uwolnioną w następującej reakcji spontanicznego rozszczepienia:
238U → 95Sr + 140Xe + 3n
przy założeniu, że masy atomów wynoszą m(238U) = 238.050784 u, m(95Sr) = 94,919388 u, m(140Xe) = 139,921610 u, oraz m(n) =1,008665 u.
Strategia
Jak zawsze, uwolniona energia jest równa masie zniszczonej razy c2, więc musimy znaleźć różnicę w masie między macierzystym 238U a produktami rozszczepienia.
Rozwiązanie
Produkty mają całkowitą masę
Utrata masy to masa 238U minus mproduktów, czyli
Dyskusja
W tym przykładzie pojawia się kilka ważnych rzeczy. Uwolniona energia 171 MeV jest duża, ale nieco mniejsza niż wcześniej szacowane 240 MeV. Dzieje się tak dlatego, że w tej reakcji rozszczepienia powstają neutrony, a nie następuje rozszczepienie jądra na dwie równe części. Rozszczepienie danego nuklidu, np. 238U , nie zawsze daje takie same produkty. Rozszczepienie jest procesem statystycznym, w którym powstaje cały szereg produktów z różnym prawdopodobieństwem. W większości rozszczepień powstają neutrony, choć ich liczba zmienia się przy każdym rozszczepieniu. Jest to niezwykle ważny aspekt rozszczepienia, ponieważ neutrony mogą indukować więcej rozszczepień, umożliwiając samopodtrzymujące się reakcje łańcuchowe.
Rozszczepienie spontaniczne może wystąpić, ale zwykle nie jest to najczęstszy tryb rozpadu dla danego nuklidu. Na przykład, 238U może ulec spontanicznemu rozszczepieniu, ale rozpada się głównie przez emisję α. Kluczowe znaczenie ma rozszczepienie indukowane neutronami, co widać na rysunku 2. Ponieważ neutrony są bezładne, nawet niskoenergetyczne mogą uderzyć w jądro i zostać zaabsorbowane, gdy poczują przyciągającą siłę jądrową. Duże jądra są opisywane przez model kropli cieczy z napięciem powierzchniowym i trybami oscylacyjnymi, ponieważ duża liczba nukleonów zachowuje się jak atomy w kropli. Neutron jest przyciągany, a więc oddaje energię, powodując odkształcenie jądra jak kropli cieczy. Jeśli jest wystarczająco rozciągnięte, jądro zwęża się w środku. Zmniejsza się liczba stykających się nukleonów i siła siły jądrowej wiążącej jądro ze sobą. Odpychanie kulombowskie pomiędzy dwoma końcami jądra powoduje jego rozszczepienie, które rozpada się jak kropla wody na dwa duże kawałki i kilka neutronów. Rozszczepienie wywołane neutronami można zapisać jako
n + AX → FF1 + FF2 + xn,
gdzie FF1 i FF2 to dwa jądra pochodne, zwane fragmentami rozszczepienia, a x to liczba wyprodukowanych neutronów. Najczęściej masy fragmentów rozszczepienia nie są jednakowe. Większość uwolnionej energii idzie na energię kinetyczną fragmentów rozszczepienia, a pozostała część na neutrony i stany wzbudzone fragmentów. Ponieważ neutrony mogą indukować rozszczepienie, możliwa jest samopodtrzymująca się reakcja łańcuchowa, pod warunkiem, że średnio produkowany jest więcej niż jeden neutron – to znaczy, jeśli x>1 w n + AX → FF1 + FF2 + xn. Widać to również na rysunku 3. Przykładem typowej reakcji rozszczepienia indukowanego neutronami jest
n+{}_{tekstekst{92}}^{tekst{235}}}U}+{}_{tekst{56}}^{tekst{142}}}Ba}+{}_{tekst{36}}^{tekst{91}}}Kr}+3}tekst{n}}.
Zauważmy, że w tym równaniu całkowity ładunek pozostaje taki sam (jest zachowany): 92 + 0 = 56 + 36. Również, jeśli chodzi o liczby całkowite, masa jest stała: 1 + 235 = 142 + 91 + 3. Nie jest to prawdą, gdy rozpatrujemy masy z dokładnością do 6 lub 7 miejsc znaczących, jak w poprzednim przykładzie.

Rysunek 2. Pokazane jest rozszczepienie indukowane neutronami. Najpierw w to duże jądro zostaje włożona energia, gdy pochłania ono neutron. Działając jak uderzona kropla cieczy, jądro deformuje się i zaczyna się zwężać w środku. Ponieważ mniej nukleonów jest w kontakcie, odpychająca siła Coulomba jest w stanie rozbić jądro na dwie części, przy czym niektóre neutrony również odlatują.

Ryc. 3. Reakcja łańcuchowa może wytworzyć samopodtrzymujące się rozszczepienie, jeśli każde rozszczepienie wytwarza wystarczającą ilość neutronów, aby wywołać co najmniej jeszcze jedno rozszczepienie. Zależy to od kilku czynników, w tym od tego, ile neutronów powstaje w przeciętnym rozszczepieniu i jak łatwo jest doprowadzić do rozszczepienia danego typu nuklidu.
Nie każdy neutron wyprodukowany w wyniku rozszczepienia wywołuje rozszczepienie. Niektóre neutrony uciekają z materiału rozszczepialnego, a inne oddziałują z jądrem nie powodując jego rozszczepienia. Możemy zwiększyć liczbę rozszczepień produkowanych przez neutrony posiadając dużą ilość materiału rozszczepialnego. Minimalna ilość potrzebna do samopodtrzymującego się rozszczepienia danego nuklidu nazywana jest jego masą krytyczną. Niektóre nuklidy, takie jak 239Pu, produkują więcej neutronów na jedno rozszczepienie niż inne, takie jak 235U . Ponadto, niektóre nuklidy są łatwiejsze do rozszczepienia niż inne. W szczególności, 235U i 239Pu, są łatwiejsze do rozszczepienia niż znacznie bardziej obfite 238U . Oba czynniki wpływają na masę krytyczną, która jest najmniejsza dla 239Pu.
Powodem 235U i 239Pu są łatwiejsze do rozszczepienia niż 238U jest to, że siła jądrowa jest bardziej atrakcyjna dla parzystej liczby neutronów w jądrze niż dla nieparzystej liczby. Rozważmy, że {}_{tekst{92}}^{tekst{235}}{{U}} {{143}}} ma 143 neutrony, a {}_{tekst{94}}^{tekst{239}}{{P}}} {{tekst{145}}} ma 145 neutronów, podczas gdy {}_{tekst{92}}^{tekst{238}}{{U}}} {{146}}}} ma 146. Gdy neutron napotka jądro z nieparzystą liczbą neutronów, siła jądrowa jest bardziej atrakcyjna, ponieważ dodatkowy neutron wyrówna tę liczbę. W powstałym jądrze odkłada się około 2-MeV więcej energii niż w przypadku, gdyby liczba neutronów była już parzysta. Ta dodatkowa energia powoduje większą deformację, co zwiększa prawdopodobieństwo rozszczepienia. Dlatego 235U i 239Pu są lepszymi paliwami rozszczepialnymi. Izotop 235U stanowi tylko 0,72% naturalnego uranu, 238U – 99,27%, a 239Pu nie występuje w przyrodzie. Największe złoża uranu na świecie posiada Australia, gdzie znajduje się 28% wszystkich złóż. Następne w kolejności są Kazachstan i Kanada. USA ma tylko 3% światowych rezerw.
Większość reaktorów rozszczepieniowych wykorzystuje 235U , który jest oddzielony od 238U pewnym kosztem. Nazywa się to wzbogacaniem. Najbardziej powszechną metodą separacji jest dyfuzja gazowa sześciofluorku uranu (UF6) przez membrany. Ponieważ 235U ma mniejszą masę niż 238U, jego cząsteczki UF6 mają większą średnią prędkość w tej samej temperaturze i dyfundują szybciej. Inną interesującą cechą 235U jest to, że preferencyjnie pochłania on bardzo wolno poruszające się neutrony (o energiach rzędu ułamków eV), podczas gdy w reakcjach rozszczepienia powstają neutrony prędkie o energiach rzędu MeV. Aby zbudować samopodtrzymujący się reaktor rozszczepiający z 235U , konieczne jest więc spowolnienie („termalizacja”) neutronów. Woda jest bardzo skuteczna, ponieważ neutrony zderzają się z protonami w cząsteczkach wody i tracą energię. Rysunek 4 przedstawia schemat konstrukcji reaktora, zwanego reaktorem wodnym ciśnieniowym.

Rysunek 4. Reaktor wodny ciśnieniowy jest sprytnie zaprojektowany, aby kontrolować rozszczepienie dużych ilości 235U , jednocześnie wykorzystując ciepło wytworzone w reakcji rozszczepienia do wytworzenia pary do generowania energii elektrycznej. Pręty regulacyjne dostosowują strumień neutronów tak, aby uzyskać krytyczność, ale jej nie przekroczyć. W przypadku przegrzania reaktora i wygotowania wody reakcja łańcuchowa zostaje przerwana, ponieważ woda jest potrzebna do termalizacji neutronów. Ta nieodłączna cecha bezpieczeństwa może zostać przeciążona w ekstremalnych okolicznościach.
Do regulacji strumienia neutronów stosuje się pręty kontrolne zawierające nuklidy, które bardzo silnie pochłaniają neutrony. Aby wytworzyć dużą moc, reaktory zawierają setki do tysięcy mas krytycznych, a reakcja łańcuchowa łatwo staje się samopodtrzymująca, co jest stanem zwanym krytycznością. Strumień neutronów powinien być starannie regulowany, aby uniknąć wykładniczego wzrostu liczby rozszczepień, co jest stanem zwanym nadkrytycznością. Pręty kontrolne pomagają zapobiec przegrzaniu, a być może nawet stopieniu lub wybuchowemu demontażowi. Woda używana do termalizacji neutronów, niezbędnej do wywołania rozszczepienia w 235U i osiągnięcia krytyczności, stanowi ujemne sprzężenie zwrotne dla wzrostu temperatury. W przypadku przegrzania reaktora i zagotowania wody do pary lub jego uszkodzenia, brak wody zabija reakcję łańcuchową. Radioaktywne produkty rozszczepienia w reaktorze mogą jednak nadal generować znaczne ilości ciepła. Dlatego w razie awarii związanej z utratą chłodziwa należy zastosować inne środki bezpieczeństwa, w tym pomocnicze pompy i wodę chłodzącą.
Przykład 2. Obliczanie energii z kilograma paliwa rozszczepialnego
Oblicz ilość energii wytworzonej przez rozszczepienie 1,00 kg 235U , biorąc pod uwagę, że średnia reakcja rozszczepienia 235U wytwarza 200 MeV.
Strategia
Całkowita wytworzona energia to liczba atomów 235U razy podana energia na rozszczepienie 235 U. Powinniśmy zatem znaleźć liczbę atomów 235U w 1,00 kg.
Rozwiązanie
Liczba atomów 235U w 1,00 kg to liczba Avogadro’a razy liczba moli. Jeden mol 235U ma masę 235,04 g; jest więc (1000 g)/(235,04 g/mol) = 4,25 mol. Liczba atomów 235U wynosi zatem,
left(4,25 mol} = 6,02 razy {10}^{23}{}^{235}}}^^{U/mol} =2.56times {10}^{24}{}^}text{ 235}}{U}}}}.
Więc całkowita uwolniona energia wynosi
begin{array}{lll}E & =& \left(2.56 razy {10}^{24}{}^{235}}{}}text{U}} \right} \left(\frac{200}text{ MeV}}{{}^{}text{235}}}{}}text{U}} \right} \left(\frac{1.60 razy {10}^{-13}}{}}}text{J}}{}}}right} \} & =& 8.21 razy {10}^{13}} J}} end{array}
Dyskusja
Jest to kolejna imponująco duża ilość energii, równoważna około 14 000 baryłek ropy naftowej lub 600 000 galonów benzyny. Jest to jednak tylko jedna czwarta energii wytworzonej w wyniku fuzji kilogramowej mieszaniny deuteru i trytu, jak pokazano w przykładzie 1. Obliczanie energii i mocy z fuzji jądrowej. Chociaż każda reakcja rozszczepienia daje około dziesięć razy więcej energii niż reakcja syntezy jądrowej, to jednak energia z kilograma paliwa rozszczepieniowego jest mniejsza, ponieważ na kilogram ciężkich nuklidów przypada znacznie mniej moli. Paliwo rozszczepieniowe jest również znacznie bardziej deficytowe niż paliwo termojądrowe, a mniej niż 1% uranu (235U) można łatwo wykorzystać.
Jednym z nuklidów, o którym już wspomniano, jest 239Pu, który ma okres połowicznego zaniku 24 120 lat i nie występuje w przyrodzie. Pluton-239 jest wytwarzany z 238U w reaktorach i daje możliwość wykorzystania pozostałych 99% naturalnego uranu jako źródła energii. W wyniku następującej sekwencji reakcji, zwanej hodowlą, powstaje 239Pu. Hodowla rozpoczyna się od wychwytu neutronu przez 238U :
Uran-239 następnie rozpada się β-:
239U → 239Np + β- + ve(t1/2 = 23 min).
Neptunium-239 również ulega rozpadowi β-:
239Np → 239Pu + β- + ve(t1/2 = 2,4 d).
Pluton-239 gromadzi się w paliwie reaktorowym z szybkością zależną od prawdopodobieństwa wychwytu neutronów przez 238U (całe paliwo reaktorowe zawiera więcej 238U niż 235U). Reaktory zaprojektowane specjalnie do produkcji plutonu nazywane są reaktorami powielającymi (breeder reactors). Wydaje się, że są one z natury bardziej niebezpieczne niż reaktory konwencjonalne, ale nie wiadomo, czy ich zagrożenia mogą być ekonomicznie akceptowalne. Cztery reaktory w Czarnobylu, w tym ten, który uległ zniszczeniu, zostały zbudowane w celu hodowli plutonu i produkcji energii elektrycznej. Reaktory te miały konstrukcję znacznie różniącą się od przedstawionego powyżej reaktora wodnego ciśnieniowego. Pluton-239 ma przewagę nad 235U jako paliwo reaktorowe – wytwarza średnio więcej neutronów na jedno rozszczepienie, a neutron termiczny łatwiej może spowodować jego rozszczepienie. Jest też chemicznie różny od uranu, więc z natury rzeczy łatwiej go oddzielić od rudy uranowej. Oznacza to, że 239Pu ma szczególnie małą masę krytyczną, co jest zaletą w przypadku broni jądrowej.
PhET Explorations: Nuclear Fission
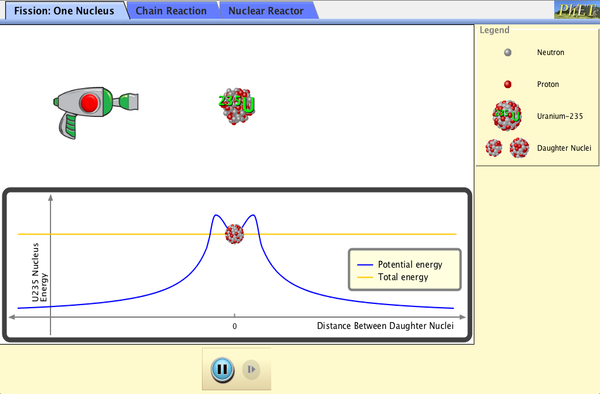
Kliknij, aby pobrać symulację. Uruchom przy użyciu języka Java.
Podsumowanie sekcji
- Rozszczepienie jądra atomowego to reakcja, w której jądro ulega rozszczepieniu.
- Rozszczepienie uwalnia energię, gdy ciężkie jądra są rozszczepiane na jądra o średniej masie.
- Samoistne rozszczepienie jest możliwe, ponieważ rozszczepienie indukowane neutronami wytwarza neutrony, które mogą indukować inne rozszczepienia, n + AX → FF1 + FF2 + xn, gdzie FF1 i FF2 są dwoma jądrami pochodnymi lub fragmentami rozszczepienia, a x jest liczbą wyprodukowanych neutronów.
- W celu osiągnięcia krytyczności powinna być obecna minimalna masa, zwana masą krytyczną.
- Więcej niż masa krytyczna może wytworzyć nadkrytyczność.
- Produkcja nowych lub różnych izotopów (zwłaszcza 239Pu) w wyniku przemian jądrowych nazywa się hodowlą, a reaktory przeznaczone do tego celu są nazywane reaktorami powielającymi.
Pytania pojęciowe
- Wyjaśnij, dlaczego rozszczepienie ciężkich jąder uwalnia energię. Podobnie, dlaczego do rozszczepienia lekkich jąder wymagany jest nakład energii?
- Wyjaśnij, z punktu widzenia zachowania pędu i energii, dlaczego zderzenia neutronów z protonami lepiej termalizują neutrony niż zderzenia z tlenem.
- Ruiny reaktora w Czarnobylu są zamknięte w ogromnej betonowej konstrukcji zbudowanej wokół niego po wypadku. W zimie do budynku przenika trochę deszczu, a radioaktywność z budynku wzrasta. Co to sugeruje, że dzieje się w środku?
- Ponieważ jądro uranu lub plutonu rozpada się na kilka fragmentów rozszczepienia, których rozkład masy obejmuje szeroki zakres kawałków, czy spodziewałbyś się większej radioaktywności resztkowej z rozszczepienia niż z syntezy? Wyjaśnij.
- Rdzeń reaktora jądrowego wytwarza dużą ilość energii cieplnej z rozpadu produktów rozszczepienia, nawet gdy wytwarzająca energię reakcja łańcuchowa rozszczepienia jest wyłączona. Czy to ciepło resztkowe będzie największe po długim czy krótkim czasie pracy reaktora? A jeśli reaktor był wyłączony przez wiele miesięcy?
- Jak reaktor jądrowy może zawierać wiele mas krytycznych i nie przejść w stan nadkrytyczny? Jakie metody są stosowane do kontroli rozszczepienia w reaktorze?
- Dlaczego ciężkie jądra z nieparzystą liczbą neutronów mogą być pobudzane do rozszczepienia za pomocą neutronów termicznych, podczas gdy te z parzystą liczbą neutronów wymagają większego nakładu energii do wywołania rozszczepienia?
- Dlaczego konwencjonalny reaktor jądrowy z rozszczepieniem nie jest w stanie wybuchnąć jako bomba?
Problemy &Ćwiczenia
1. (a) Oblicz energię uwolnioną w rozszczepieniu indukowanym neutronami (podobnie jak w rozszczepieniu spontanicznym w przykładzie 1. Obliczanie energii uwolnionej w wyniku rozszczepienia)
przy założeniu, że m(96Sr) = 95,921750 u i m(140Xe) = 139,92164. (b) Wynik ten jest o około 6 MeV większy od wyniku dla rozszczepienia samorzutnego. Dlaczego? (c) Potwierdź, że całkowita liczba nukleonów i całkowity ładunek są w tej reakcji zachowane.
2. (a) Oblicz energię uwolnioną w reakcji rozszczepienia indukowanego neutronami
given m(92Kr) = 91.926269 u i m(142Ba) = 141.916361 u.
(b) Potwierdź, że całkowita liczba nukleonów i całkowity ładunek są w tej reakcji zachowane.
3. a) Oblicz energię uwolnioną w reakcji rozszczepienia indukowanego neutronami
given m(96Sr) = 95,921750 u and m(140Ba) = 139,910581 u.
(b) Potwierdź, że w tej reakcji całkowita liczba nukleonów i całkowity ładunek są zachowane.
4. Potwierdź, że każda z wymienionych reakcji dla hodowli plutonu przebiega tuż po przykładzie 2. Obliczanie energii z kilograma paliwa rozszczepialnego zachowuje całkowitą liczbę nukleonów, całkowity ładunek i liczbę rodziny elektronów.
5. Hodowla plutonu produkuje energię nawet przed rozszczepieniem plutonu. (Głównym celem czterech reaktorów jądrowych w Czarnobylu była hodowla plutonu na potrzeby broni. Energia elektryczna była produktem ubocznym wykorzystywanym przez ludność cywilną). Obliczcie energię powstałą w każdej z wymienionych reakcji hodowli plutonu, postępując zgodnie z przykładem 2. Obliczanie energii z kilograma paliwa rozszczepialnego. Odpowiednie masy wynoszą: m(239U) = 239,054289 u, m(239Np) = 239,052932 u, i m(239Pu) = 239,052157 u.
6. Naturalnie występujący izotop promieniotwórczy 232Th nie jest dobrym paliwem rozszczepialnym, ponieważ ma parzystą liczbę neutronów; można go jednak wyhodować na odpowiednie paliwo (podobnie jak 238U jest wyhodowany na 239P).
(a) Czym są Z i N dla 232Th?
(b) Napisz równanie reakcji dla neutronu wychwyconego przez 232Th i zidentyfikuj nuklid AX powstały w reakcji n + 232Th → AX + γ.
(c) Jądro produktu β- rozpada się, podobnie jak jego córka. Napisz równania rozpadu dla każdego z nich i zidentyfikuj jądro końcowe.
(d) Potwierdź, że jądro końcowe ma nieparzystą liczbę neutronów, co czyni je lepszym paliwem rozszczepieniowym.
(e) Sprawdź okres połowicznego zaniku jądra końcowego, aby przekonać się, czy żyje ono wystarczająco długo, aby być użytecznym paliwem.
7. Moc elektryczna dużego reaktora jądrowego wynosi 900 MW. Ma on sprawność 35,0% w przetwarzaniu energii jądrowej na elektryczną.
(a) Jaka jest moc cieplna reaktora jądrowego w megawatach?
(b) Ile jąder 235U rozszczepia się w każdej sekundzie, zakładając, że średnie rozszczepienie wytwarza 200 MeV?
(c) Jaka masa jąder 235U ulega rozszczepieniu w ciągu jednego roku pracy przy pełnej mocy?
8. Duży reaktor energetyczny pracujący od kilku miesięcy został wyłączony, ale aktywność resztkowa w rdzeniu nadal wytwarza 150 MW mocy. Jeżeli średnia energia na rozpad produktów rozszczepienia wynosi 1,00 MeV, to jaka jest aktywność rdzenia w curiach?
Słowniczek
reaktory powielające: reaktory zaprojektowane specjalnie do produkcji plutonu powielanie: proces reakcji, w wyniku którego powstaje 239Pu krytyczność: stan, w którym reakcja łańcuchowa łatwo staje się samopodtrzymująca się masa krytyczna: minimalna ilość niezbędna do samopodtrzymującego się rozszczepienia danego nuklidu fragmenty rozszczepienia: jądra pochodne model ciekłej kropli: model jądra (tylko dla zrozumienia niektórych jego cech), w którym nukleony w jądrze zachowują się jak atomy w kropli rozszczepienie jądra: reakcja, w której jądro rozszczepia się rozszczepienie wywołane neutronem: rozszczepienie zainicjowane po absorpcji neutronu nadkrytyczność: wykładniczy wzrost liczby rozszczepień
Wybrane rozwiązania problemów & Ćwiczenia
1. (a) 177,1 MeV (b) Ponieważ wzmocnienie neutronu zewnętrznego daje około 6 MeV, co jest średnią BE/A dla ciężkich jąder. (c) A = 1 + 238 = 96 + 140 + 1 + 1 + 1, Z = 92 = 38 + 53, efn = 0 = 0
3. (a) 180,6 MeV (b) A = 1 + 239 = 96 + 140 + 1 + 1 + 1, Z = 94 = 38 + 56, efn = 0 = 0
5. 238U + n → 239U + γ 4.81 MeV
239U → 239Np + β- + ve 0,753 MeV
239Np → 239Pu + β- + ve 0,211 MeV
7. a) 2,57 × 103 MW b) 8,03 × 1019 rozszczepień/s c) 991 kg
.