Jednym z ważnych pytań jest, jak liczby pierwsze są rozmieszczone wśród liczb całkowitych? Odpowiedź brzmi, w bardzo krótkich słowach, raczej losowo, biorąc pod uwagę pewne podstawowe statystyki…
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Kanada
Email Bill Casselman
| |
|
Wprowadzenie
Wiele lat temu wysunięto przypuszczenie, że istnieje nieskończona liczba par liczb pierwszych $p$, $q$ z $q = p+2$. Ostatnio poczyniono pewne postępy w tej sprawie (i to sławne). Powiem niewiele o ostatnich postępach, ale zamiast tego omówię, czego się spodziewamy – a nie co wiemy – o takich parach. Nic, co powiem, nie jest nowe i do pewnego stopnia tylko rozwinąłem to, co Andrew Granville mówi w swoim niedawnym komentarzu na temat ostatnich postępów.
Ilu liczb pierwszych możemy się spodziewać?
Liczba pierwsza to dodatnia liczba całkowita, która nie ma dzielników poza sobą i $1$. Definicja jest prosta, ale jak tylko zaczniemy badać znaczenie liczb pierwszych, zdamy sobie sprawę, że wykazują one wiele subtelnych zachowań. Jednym z ważnych pytań jest, jak liczby pierwsze są rozmieszczone wśród liczb całkowitych? Odpowiedź brzmi, w bardzo krótkich słowach, raczej losowo, biorąc pod uwagę pewne podstawowe statystyki. Co przez to rozumiem?
No cóż, oto kwadratowa tablica przedstawiająca wszystkie liczby pierwsze do 400$:

W tablicy tej występują pewne wzorce, z których niektóre skomentuję później. Większość z tych, które dostrzegasz, jest spowodowana przez jakiś artefakt wyświetlacza. Na przykład, co druga kolumna jest w zasadzie pusta, a to dlatego, że jedynym parzystym prime jest $2$. Również, co piąta kolumna jest w zasadzie pusta. Bardziej interesujące są bliźniacze pary prime (niektóre z nich nie są tak widoczne, ponieważ dzielą się na dwa rzędy, takie jak $59$, $61$), a także pewne wzory związane z ostatnimi wyświetlanymi cyframi. Są to, co można nazwać lokalnymi wzorami. Nie są widoczne żadne globalne.
Wiele wysiłku włożono w niezwykle wydajne sposoby tworzenia liczb pierwszych, ale w dzisiejszych czasach nawet bardzo prosty program zajmuje tylko niewielką ilość czasu, aby stworzyć duże listy liczb pierwszych. Jeden z najbardziej owocnych programów będzie zrobić dużą listę primes, a następnie użyć tego do obliczenia funkcji $pi(n)$, liczba primes $ n$.
Jedną z rzeczy, które mogą być używane do jest, aby uzyskać przybliżone pojęcie o częstotliwości primes. W przedziale $$ jest 135$ primes:
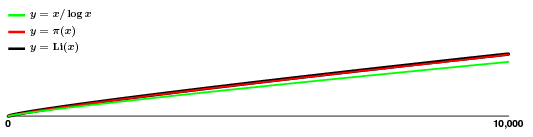
Przybliżenie wygląda świetnie! Tak więc, nawet jeśli $pi(x)$ odbija się trochę wokół, najwyraźniej bez większego wzoru, mamy dość dobre oszacowanie dla niego, co oznacza, że mamy dobre pojęcie o tym, jak rosną liczby pierwsze, przynajmniej średnio.
Należy jednak pamiętać, że pozorna gładkość jest zwodnicza. Z bliska, oto jak wyglądają dwie górne krzywe:

Komentarze?
Heurystyczne rozumowanie o bliźniaczych prymach
Pierwiastki bliźniacze to para $p$, $p+2$, które są jednocześnie prymami. Na przykład, z jednej z powyższych działek widzimy bliźniacze prymitywy $$ , , , , , , , , $$
i inne. Przypuszcza się, że jest ich nieskończenie wiele, ale chociaż istnieje na to wiele empirycznych dowodów, nie zostały one jeszcze udowodnione.
Prawdopodobnie najmocniejszym dowodem jest wzór, który przybliża liczbę $pi_{2}(x)$ bliźniaczych pierwiastków $$ nadzwyczaj dobrze. Nie jestem do końca pewien pochodzenia tego wzoru, ale po raz pierwszy pojawił się on w pracy G. H. Hardy’ego i J. E. Littlewooda (sami są parą bliźniaczych pierwiastków) z 1923 roku. Praca zawiera kilka podobnych wzorów, wszystkie oparte na tej samej metodzie, której używali do rozwiązywania wielu problemów wcześniej. Była to ich metoda kołowa. Ich wyprowadzenie wzoru na $pi_{2}(x)$ nie jest wcale rygorystyczne, ale jest bardzo przekonujące. Zwięzła relacja na ten temat znajduje się w załączniku do artykułu Andrew Granville’a.
Jednak tuż po II wojnie światowej Lord Cherwell (Frederick Lindemann) zasugerował bardziej elementarne probabilistyczne (i wciąż nie rygorystyczne) wyprowadzenie. Doprowadziło to do współpracy z E. M. Wrightem i ostatecznie do pośmiertnej wspólnej publikacji. Jest to wyjaśnione w rozdziale 22.20 znanego tekstu Hardy’ego i Wrighta. Nieco bardziej elementarną wersję tego można znaleźć w dodatku do artykułu Granville’a (Sekcja 2.5). Podążam za nim.
Punktem wyjścia dla wiarygodnego rozumowania jest nasze oszacowanie dla $pi(x)$, liczby liczb pierwszych mniejszych lub równych $x$. Podstawową ideą tego wyprowadzenia jest to, że liczby pierwsze są w dużym stopniu rozmieszczone losowo. Wiemy, że w sąsiedztwie $x$ gęstość liczb pierwszych wynosi około $1/log x$. Gdyby liczby pierwsze były rozmieszczone losowo, to prawdopodobieństwo, że dowolne dwie dane liczby w pobliżu $x$ są liczbami pierwszymi, byłoby tylko iloczynem lokalnych prawdopodobieństw, czyli $1/log^{2} x$. Jest to z pewnością osobliwe rozumowanie, ponieważ jeśli $n > 2$, to prawdopodobieństwo, że zarówno $n$, jak i $n+1$ są liczbami pierwszymi wynosi $0$, podczas gdy fakt, że $p$ jest liczbą pierwszą, wydaje się zwiększać szanse, że $p+2$ nią jest. Istnieją podobne względy, które należy wziąć pod uwagę z powodu możliwej podzielności przez inne małe liczby pierwsze, również w sąsiedztwie $x$.
W tej historii jest jeden prosty fakt. Jeśli $q$ jest dowolną liczbą pierwszą, to prawdopodobieństwo wyboru losowej liczby całkowitej, która nie jest podzielna przez $q$ wynosi $1-1/q$. Prawdopodobieństwo wyboru dwóch liczb, które nie są podzielne przez $q$ jest więc iloczynem $(1 – 1/q)^{2}$. Załóżmy, że $p$ i $p+2$ są pierwszymi, to ani $p$, ani $p+2$ nie jest podzielne przez $q$. Jeśli $q = 2$, to zdarza się to w 1/2$ przypadków. Jeśli $q = 2$, to prawdopodobieństwo, że $p nie jest równe 0$ i $p nie jest równe -2$ modulo $q$ jest $(1 – 2/q)$. Z powodu twierdzenia chińskiego remanentu, podzielność przez dwie liczby pierwsze jest niezależnym wydarzeniem. Jeśli więc $x$ jest duże, a $Q$ jest względnie małe, to prawdopodobieństwo, że dowolna para liczb $m$ i $n$ w pobliżu $x$ nie będzie wielokrotnością żadnej liczby pierwszej aż do $Q$ wynosi $$ { 1 – 2/q} { (1 – 1/q)^{2} } \. $$
Niech $Gamma_{Q}$ będzie stosunkiem tego do $prod_{q \le Q}(1 – 2/q)$: $$ \Gamma_{Q} = { 1\over 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} \^{2} } $$ Mamy $$ { 1 – 2/q ^{2} { (1 – 2/q)^{2} } = { (1 – 1/q)^{2} – 1/q^{2} \{ (1 – 1/q)^{2} } } = 1 – { 1 \over (q -1)^{2} } } \$$ Standardowe kryterium mówi, że iloczyn ten jest zbieżny, jeśli zbieżna jest suma $$ 1/(q-1)^{2}$. Ale jest on zbieżny, ponieważ test całkowy mówi nam, że $suma 1/n^{2}$ jest zbieżna. Zatem iloczyn ten jest rzeczywiście zbieżny do liczby $Pi_{infty}$ w miarę jak $Q jest zbieżne. Niech $C_{2}$ będzie jego odwrotnością. Sekcja 2.5 artykułu Granville’a mówi, że intuicyjnie powinno być w tym momencie rozsądne, że liczba $pi_{2}(x)$ bliźniaczych pierwiastków $le x$ jest przybliżona przez $$ \Pi_{2}(x) = C_{2} \^{infty} { dx \over \log^{2} x } \$$
Tekst Hardy’ego i Wrighta przedstawia bardziej staranną analizę, która czyni ten intuicyjny skok nieco jaśniejszym.
Wartość stałej została obliczona dawno temu przez J. W. Wrencha na około $1.32032363169373914785562422002911155686525 $ Oto porównanie niektórych wartości $pi_{2}(x)$ i wzoru w przedziale $$: $$ \matrix{ n & 10,000 & 20,000 & 30,000 & 40,000 & 50,000 \cr \pi_{2}(n) & 205\phantom{.0} & 342 \fantom{.0} & 467 \fantom{.0} & 591 \fantom{.0} & 705 \fantom{.0} & \\Pi_{2}(x) & 214,2 & 357,7 & 486,7 & 607,4 & 722,5 \cr } $$ $ ™matrix{ n & 60,000 & 70,000 & 80,000 & 90,000 & 100,000 ™cr ™pi_{2}(n) & 811 ™fantom{.0} & 905 \fantom{.0} & 1007 \fantom{.0} & 1116 \fantom{.0} & 1224 \fantom{.0} \\Pi_{2}(x) & 833,3 & 940,9 & 1045,7 & 1148,2 & 1248,7 \cr } $$
Komentarze?
Przemyślenie Dicksona
Podwójne prymy są szczególnym przypadkiem czegoś znacznie bardziej ogólnego. Można zapytać, czy istnieje nieskończona liczba par $p$, $p+4$ lub $p$, $p+6$, które są prymami? Albo $p$, $p+10$? Przypadek par $p$ i $p+10$ jest z pewnością sugerowany przez jeden z powyższych obrazków, na którym takie pary są łatwo widoczne. A co z pewnego rodzaju trójkami? Załóżmy, że $a_{1}$, $a_{2}$, $a_{k}$ tworzą tablicę liczb całkowitych. Czy możemy się spodziewać, że istnieje nieskończona liczba zbiorów $n+a_{1}$, $n+a_{2}$, $ldots$ , $n+a_{k}$, z których wszystkie są pierwsze?
Trzeba być trochę ostrożnym. Nie ma par pierwszych w postaci $p$, $p+1$ (dawniej $p = 2$), bo jedna z tych dwóch liczb musi być podzielna przez $2$. Podobnie, w przeszłości $p = 3$ nie istnieją trójki pierwsze w postaci $p$, $p+2$, $p+4$, ponieważ jedna z nich musi być podzielna przez $3$.
Ten ostatni przykład powinien być pouczający. Liczba $p+4$ jest podzielna przez $3$ wtedy i tylko wtedy, gdy $p+1$ jest podzielne przez $3$. Zatem $3$ dzieli jedną z liczb $p$, $p+2$, $p+4$ wtedy i tylko wtedy, gdy dzieli $p$, $p+1$, $p+2$. Ale jest to pewne, gdyż ostatnia trójka wyraźnie obejmuje wszystkie liczby modulo $3$.
W ogólności mówi się, że $p$ jest przeszkodą dla tablicy $(a_{i})$, jeśli $p$ zawsze dzieli co najmniej jedną z każdego ciągu $n+a_{i}$ ($i = 1$, $ldots$, $k$). Dzieje się tak wtedy i tylko wtedy, gdy liczby $a_{i} ∗; {mod} \p$ wypełniają całe $Z/p$.
Nigdy nie może się to zdarzyć, jeśli $p > k$, więc aby sprawdzić, czy jakieś $p$ przeszkadza $(a_{i})$ musimy tylko sprawdzić, czy $a_{i}$ pokrywają $Z/p$ dla wszystkich $p k$. Tablicę $(a_{i})$ nazywamy dopuszczalną, jeśli nie ma ona żadnych przeszkód pierwszorzędnych.
Na przykład $(1,3,7,9)$ jest tablicą dopuszczalną, gdyż, jak łatwo sprawdzić, ani $2$ ani $3$ nie są przeszkodami. Kilka ciągów pierwszych pasujących do tego wzoru można zobaczyć na jednym z diagramów powyżej. Inne przykłady to (a) dowolne $0$, $2n$; (b) $0$, $4$, $6$; (c) $0$, $2$, $6$.
Istnieją arbitralnie duże zbiory dopuszczalne. W rzeczywistości:
Twierdzenie. Jeśli $a_{1}$ do $a_{k}$ jest dowolnym zbiorem różnych liczb pierwszych $> k$, to tworzą one zbiór dopuszczalny.
Dlaczego tak jest? Jeśli $p$ jest dowolną liczbą pierwszą, gdzie $p> k$, to widzieliśmy już, że nie może być przeszkodą. Ale jeśli $p jest k$, to nie może dzielić żadnego z $a_{i}$, z których żadne nie może być przystające do $0$ modulo $p$. Tak więc $a_{i}$ nie wypełniają $Z/p$.
Szczególnym przypadkiem przypuszczenia wysuniętego pierwotnie przez L. E. Dicksona jest to, że jeśli nie ma pierwszorzędnych przeszkód dla $(a_{i})$ to istnieje nieskończenie wiele ciągów pierwszorzędnych postaci $(n +a_{i})$.
Co się ostatnio wydarzyło
To nie jest miejsce na opowiadanie całej historii, która została dokładnie opisana w innych miejscach. Polecam szczególnie artykuł w Quancie autorstwa Erici Klarreich dla popularnej relacji, oraz esej Granville’a dla bardziej technicznej. Chcę tylko powiedzieć nieco dokładniej niż w relacji Klarreicha, co jest najsłynniejszym z nowych wyników.
Jest to zasługa Yitanga Zhanga. Najprostszym stwierdzeniem tego, co udowodnił, jest to, że istnieje nieskończona liczba przedziałów $[n, n+70 000 000)$ zawierających co najmniej dwie liczby pierwsze. Jest to słabsze niż domniemanie o bliźniaczych prymach, ale koncepcyjnie bardzo bliskie. W późniejszych pracach (prowadzonych przez wielu matematyków) wielkość luki została poważnie zmniejszona, ale przypuszczalnie nie ma sposobu, aby zredukować ją do $2$ przy użyciu obecnych metod.
Jak wyjaśnia Granville, pierwszym i prawdopodobnie głównym wynikiem Zhanga jest to, że istnieje $k$ z własnością, że jeśli $a_{1}$, $ldots$ , $a_{k}$ jest dopuszczalnym zbiorem $k$ elementów, to istnieje nieskończenie wiele $n$ takich, że $n +a_{i} \$ zawiera co najmniej dwie liczby pierwsze. (W artykule Klarreicha w Quancie macierz taka nazywana jest „grzebieniem”. Należy pamiętać, że zgodnie z domysłem Dicksona, oczekiwalibyśmy, że będziemy w stanie powiedzieć, że wszystkie $k$ są liczbami pierwszymi). W rzeczywistości Zhang udowodnił, że to twierdzenie jest prawdziwe dla pewnego $k =3 500 000$ rozciągającego się na przedział 70 000 000$. Słynną już konsekwencją jest to, że dla pewnych $m = 70 000 000$ istnieje nieskończenie wiele par liczb pierwszych $p$, $p+m$.
Czytaj dalej
- Lord Cherwell i E. M. Wright, „The frequency of prime patterns”, The Quarterly Journal of Mathematics 11 (1960).
Ci, którzy wiedzą coś o życiu Lorda Cherwella, znanego inaczej jako Frederick Lindemann, będą bardzo zaskoczeni, gdy dowiedzą się o jego wkładzie w teorię liczb. Biografia w Wikipedii nie sugeruje odpowiednio wszystkich przyczyn jego złej reputacji jako głównego doradcy naukowego Churchilla podczas II wojny światowej.
- L. E. Dickson, „A new extension of Dirichlet’s theorem on prime numbers”, Messenger of Mathematics 33.
Zobacz też wpis w Wikipedii na temat domysłu Dicksona.
- Andrew Granville, „Primes in intervals of bounded length”. Dostępne na jego stronie domowej.
- G. H. Hardy, Ramanujan, Cambridge University Press.
Sekcja 2.5 zawiera idealne wyprowadzenie możliwego wzoru na $pi(x)$.
- G. H. Hardy i J. E. Littlewood, „Some problems of 'Partitio numerorum’ III: on the expression of a number as a sum of primes”, Acta Mathematica 44 (1923).
- G. H. Hardy and E. M. Wright, The theory of numbers, Oxford Press.
- Erica Klarreich, „Together and alone, closing the prime gap”, Quanta November 19, 2013.
- B. Riemann, „On the number of prime numbers less than a given quantity” (O liczbie liczb pierwszych mniejszych od danej wielkości). Angielski przekład tego klasyka autorstwa Davida Wilkinsa jest dostępny pod linkiem w Wikipedii.
Między innymi szkicuje on wyprowadzenie przybliżonego wzoru na $pi(x)$.
- J. W. Wrench, „Evaluation of Artin’s constant and the twin-prime constant”, Mathematics of Computation 76 (1961).
Wczesne obliczenie $C_{2}$.
- Listy liczb pierwszych do $1,000,000,000$
- Lista pierwszych 20,000 liczb bliźniaczych.
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman
.