GENERAL CHEMISTRY TOPICS
Energy: Foundational concepts
Formy energii: Kinetyczna i potencjalna.Praca i energia.Ciepło i temperatura.Elektrostatyczna energia potencjalna.
Energia: kinetyczna i potencjalna
Pojęcie energii jest fundamentalne dla nauk fizycznych. W tym miejscu chcemy przedstawić kilka pierwszych zasad dotyczących energii, a także wprowadzić niektóre z form, jakie przyjmuje energia, które są szczególnie ważne dla chemii. Po pierwsze, często bardzo przydatne jest zdefiniowanie systemu jako konkretnej części wszechświata, na której dokonywane są nasze obserwacje. System składa się z obiektu lub zbioru obiektów, i jest odróżniony od reszty wszechświata – który nazywamy otoczeniem – przez rzeczywistą lub urojoną granicę.
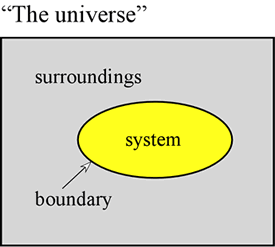
Próbka gazu trzymana w stałej objętości, takiej jak metalowy cylinder, jest przykładem systemu – takiego, który będzie dla nas istotny, gdy podejmiemy się badania ogólnych właściwości gazów. Kolejnymi przykładami są: próbka gazu w balonie lub mieszanka paliwowa w cylindrze z tłokiem. W obu tych przypadkach układ jest zamknięty fizyczną, ale ruchomą granicą, a więc objętość układu nie jest stała. Dodatkowym przykładem, który będziemy często rozważać, jest mieszanina substancji w roztworze przechodząca reakcję chemiczną w probówce lub zlewce. Terminologia wprowadzona tutaj ma szczególne znaczenie w badaniu, w jaki sposób energia przejawia się w systemach chemicznych, co w dużej mierze należy do termodynamiki.
W chemii ogólnej, systemy, które uważamy za istotne są zazwyczaj w spoczynku i efekty grawitacyjne są ignorowane. Często najbardziej interesują nas układy, w których zachodzą reakcje chemiczne, a skład chemiczny układu zmienia się w czasie. Przyjmijmy jednak na razie szerszą perspektywę, używając systemów mechanicznych, takich jak wahadło lub kule bilardowe toczące się i zderzające, aby pomóc nam zrozumieć ogólne zasady odnoszące się do energii.
Można powiedzieć, że system posiada energię na dwa różne sposoby, które nazywamy energią kinetyczną i potencjalną. Energia kinetyczna jest energią materii w ruchu. Fizyka dostarcza dokładnej matematycznej definicji energii kinetycznej (KE), pokazanej w równaniu (poniżej po lewej).
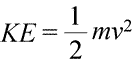
Tutaj, energia kinetyczna obiektu jest reprezentowana jako iloczyn masy obiektu (m) i kwadratu jego prędkości (v), pomnożony również przez stałą ½. Jeśli układ składa się z więcej niż jednego obiektu, całkowita energia kinetyczna jest wyrażalna jako suma energii kinetycznych poszczególnych obiektów.
Możemy wyprowadzić jednostki dla energii biorąc pod uwagę tę definicję. Jednostką energii w układzie SI jest dżul (J), który jest zdefiniowany jako:
1 J = 1 kg-m-s-2
Energia potencjalna jest energią systemu, która zazwyczaj może być przekształcona w energię kinetyczną w jakiejś formie i zdolna do wytworzenia, w jakiejś mierze, wielkości zwanej pracą (omówioną dalej). Wyraźnym przykładem energii potencjalnej jest cegła na gzymsie budynku. Cegła ta posiada pewną ilość energii potencjalnej z racji swojej wysokości – położenia względem pola grawitacyjnego. Jeśli damy cegiełce kuksańca, aby spadła z gzymsu, to spontanicznie przesunie się ona w kierunku niższej grawitacyjnej energii potencjalnej i w ten sposób zyska energię kinetyczną. Innym przykładem jest elektryczna energia potencjalna baterii (która jest wyrażona w postaci napięcia). Kiedy obwód jest wykonany z przewodem i żarówką, łącząc dwa zaciski baterii, różnica potencjałów elektrycznych między nimi powoduje ruch elektronów w przewodzie (energia kinetyczna), co skutkuje produkcją zarówno ciepła, jak i światła.
Ważną ogólną zasadą dotyczącą energii jest to, że nie może być ona ani stworzona, ani zniszczona. Jest to znane jako prawo zachowania energii. Ilościowo oznacza to, że w systemie takim jak spadająca cegła lub wahadło zegara, suma energii kinetycznej i potencjalnej jest stała. Jest to w pewnym sensie abstrakcja, ponieważ w prawdziwym wahadle część energii jest stale tracona z powodu tarcia, a niewielka ilość energii musi być dodawana do wahadła, aby utrzymać jego wahanie (i działanie zegara). Ale jeśli uwzględnimy taką „utraconą” energię (która w rzeczywistości pojawia się jako wzrost energii cieplnej otaczających cząsteczek powietrza) poprzez staranne pomiary eksperymentalne, okaże się, że w istocie energia jest zawsze zachowana. Inne zastrzeżenie jest podsumowane w słynnym równaniu Einsteina E = mc2, które wyraża fundamentalną równoważność masy i energii. Bardziej ogólna forma prawa zachowania energii, którą można nazwać prawem zachowania masy-energii, uwzględnia tę równoważność. Wracając do chemii ogólnej, takie materia-energia interkonwersje nie są typowo jej domeną, podczas gdy badanie reakcji jądrowych i radioaktywności jest objęte fizyką jądrową.
Jeśli rozważymy reakcję chemiczną, w której zmianom chemicznym towarzyszy produkcja ciepła, pojawia się pytanie: Co z zachowaniem energii w tym przypadku? Odpowiedź jest taka, że istnieje pewna forma energii potencjalnej, którą możemy nazwać chemiczną energią potencjalną (lub po prostu potencjałem chemicznym), o której można myśleć jako o rezydującej w składzie molekularnym reagentów. Ta energia potencjalna jest następnie przekształcana w energię w postaci ciepła, ale okazuje się, że ilość netto obecnej energii pozostaje stała, gdy tylko jesteśmy w stanie zdefiniować i zmierzyć produkcję ciepła. Codziennym przykładem tego, co możemy teraz rozumieć jako chemiczną energię potencjalną, jest silnik benzynowy, w którym mieszanina benzyny i tlenu posiada utajoną formę energii. Ta utajona energia w mieszaninie benzyny i tlenu jest zużywana do produkcji energii kinetycznej samochodu.
Praca i energia
Praca jest kolejnym pojęciem, które przyznaje precyzyjną definicję w fizyce. Co więcej, prawa mechaniki mogą być powiązane z energią za pomocą twierdzenia praca-energia. Kopnięcie piłki nożnej, lub dowolna liczba podobnych przykładów, ilustruje ideę, że energia kinetyczna obiektu może być zwiększona przez zastosowanie siły. Twierdzenie praca-energia, które jest uogólnieniem tej idei, można w przybliżeniu przedstawić następująco: Zmiana energii, jaką posiada obiekt, jest równa wielkości działającej na niego siły, pomnożonej przez odległość, przez którą działa ta siła.
Zmiana energii zachodząca w układzie w wyniku pracy może być dodatnia lub ujemna, z punktu widzenia układu. Praca może być wykonana przez system, lub system może mieć pracę wykonaną na nim przez otoczenie. Jeżeli praca jest wykonywana przez system, traci on energię na rzecz otoczenia. Jeśli praca jest wykonywana przez system, jego energia wzrasta. Na przykład, gdy iskra zapoczątkowująca spalanie mieszanki w cylindrze z ruchomym tłokiem powoduje gwałtowne rozprężenie układu, a rozprężenie to jest mechanicznie sprzężone z ruchem pręta w otoczeniu, układ cylindra wykonuje pracę na rzecz otoczenia i w ten sposób traci energię. Jest to oczywiście część tego, jak silnik spalinowy zamienia chemiczną energię potencjalną na energię kinetyczną poruszającego się samochodu.
Jedną z implikacji twierdzenia praca-energia jest dla jednostek, a mianowicie, że praca może być mierzona w tych samych jednostkach co energia. Ponieważ drugie prawo Newtona to siła = masa × przyspieszenie, niuton (N), jednostka SI dla siły, jest wyprowadzany jako M × L × T -2, a zatem 1 N = 1 kg m s-2. Siła razy odległość ma wielkość M × L2 × T -2, a zatem jednostkę energii w układzie SI, dżul (J), definiuje się jako 1 J = 1 kg m2 s-2. W tym momencie powinieneś sam sprawdzić, że równanie na energię kinetyczną zawiera tę samą kombinację podstawowych wielkości: masy (M), długości (lub odległości, L) i czasu (T).
Ciepło i temperatura
Słowa ciepło i temperatura używamy dość często i często mówimy o cieple jako formie energii. Wszyscy mamy intuicyjne poczucie, czym są te rzeczy, ale tutaj chcemy myśleć o nich bardziej naukowo, i dać im bardziej formalne definicje, jeśli możemy. Jest to konieczny wstęp do kwantyfikacji energii odpowiadającej ciepłu, a następnie do pomiarów w celu weryfikacji prawa zachowania energii. Stwierdzamy, że energia cieplna układu może być porównana do całkowitej energii kinetycznej (zdefiniowanej powyżej) atomów i cząsteczek wchodzących w jego skład. Temperatura obiektu lub systemu jest w rzeczywistości miarą średniej energii kinetycznej atomów i/lub molekuł wchodzących w jego skład. (N.B. Temperatura nie jest dokładnie równa średniej energii kinetycznej cząsteczek, ale jest do niej wprost proporcjonalna. Więcej szczegółów można znaleźć na stronie kinetycznej teorii molekularnej).
Jeden sposób, aby zwizualizować to, co mamy na myśli przez ciepło i temperaturę, i rozróżnienie między nimi, jest rozważenie analogii bilardowej kuli. W niektórych prostych kontekstach, zachowanie kul bilardowych są odpowiednim modelem dla zbioru atomów lub cząsteczek, takich jak w próbce gazu. Podobnie jak kule bilardowe, które zostały właśnie uderzone przez szybko poruszającą się białą bilę, cząsteczki gazu poruszają się, odbijając się od siebie nawzajem i od ścian pojemnika, w którym się znajdują. Całkowita energia kinetyczna kul bilardowych, będąca sumą indywidualnych energii kinetycznych każdej z nich, jest analogiczna do energii cieplnej zawartej w próbce cząsteczek gazu. W „break” na początku gry w bilard, początkowa energia kinetyczna bili jest podzielona między wszystkie kulki na stole. Niektóre z nich poruszają się dość szybko, a inne nie tak szybko, ale analogia do „ciepła” lub „energii cieplnej” dla układu bil bil bilardowych jest po prostu sumą tych energii kinetycznych. Z drugiej strony, temperatura systemu kul bilardowych byłaby proporcjonalna do średniej energii kinetycznej zespołu kul.
Elektrostatyczna energia potencjalna
Prawo elektrostatycznego przyciągania i odpychania, lub prawo Coulomba, opisuje siłę wywieraną na naładowany obiekt z powodu obecności innego naładowanego obiektu. Siłę tę najłatwiej jest obliczyć, gdy ładunki można traktować jako bardzo małe ładunki punktowe. Wielkość siły, którą „czuje” naładowany obiekt jest proporcjonalna do iloczynu ładunków (jednostką ładunku elektrycznego w układzie SI jest Coulomb, C) i odwrotnie proporcjonalna do kwadratu odległości między ładunkami (r na rysunku po prawej). Siła jest siłą przyciągającą (jak grawitacja, wskazana przez strzałki skierowane do wewnątrz na rysunku), jeśli ładunki są przeciwnego znaku, i odpychającą, gdy ładunki mają ten sam znak.
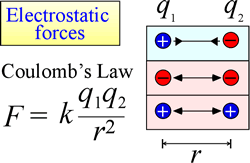
Gdy siły (takie jak siły elektrostatyczne, magnetyczne i grawitacyjne) mogą działać na odległość (przez przestrzeń, bez kontaktu mechanicznego), mówi się, że obiekty podlegające takim siłom znajdują się w polu energii potencjalnej. O grawitacyjnej energii potencjalnej mówiliśmy powyżej, i podobnie w przypadku sił elektrostatycznych, naładowany obiekt będzie posiadał elektrostatyczną energię potencjalną na mocy swojego położenia w polu elektrycznym. Takie pole istnieje w pobliżu każdego innego ładunku lub ładunków.
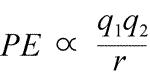
Równanie na elektrostatyczną energię potencjalną: PE jest proporcjonalna do ładunków q1 i q2, i odwrotnie proporcjonalna do odległości separacji, r. Postać funkcji energii potencjalnej wynika matematycznie z wyrażenia siły, prawa Coulomba.
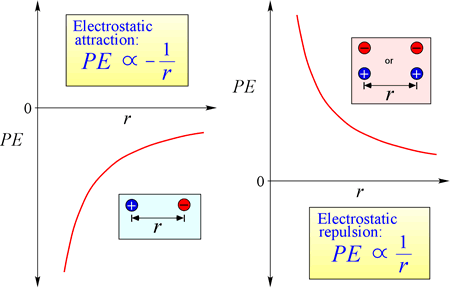
Z uwagi na przeciwne znaki ładunków w przyciąganiu, energia potencjalna jest zawsze ujemna, a im bardziej zbliżają się ładunki, tym bardziej ujemna – czyli mniejsza – staje się energia potencjalna. Gdy odległość między ładunkami, r, zbliża się do zera, energia potencjalna staje się nieskończenie ujemna. Dla ładunków o tym samym znaku, energia odpychania jest zawsze dodatnia i staje się nieskończenie dodatnia, gdy odległość separacji, r zbliża się do zera.
Elektrostatyczna energia potencjalna jest ważnym czynnikiem w chemii. Zrozumienie natury atomu, wiązanie chemiczne i siły międzycząsteczkowe są całkowicie zależne od uwzględnienia wpływu oddziaływań ładunek-ładunek, które przyczyniają się do energii układu.
Ważne jednostki
Energia (jednostka SI) 1 dżul = 1 J = 1 kg-m-s-2
Ładunek elementarny, e = 1.60218 × 10-19 C (coulomb, C)
Stała Faradaya: F = NAe = 9,64853 × 104 C-mol-1
Potencjał elektryczny: wolty, V 1 V = 1 J C-1
.