Nieczęsto zdarza się, by równanie matematyczne trafiało do krajowej prasy, a tym bardziej do popularnego radia lub, co najbardziej zdumiewające, było przedmiotem debaty w brytyjskim parlamencie. Jednak w 2003 roku stare, dobre równanie kwadratowe, o którym wszyscy uczyliśmy się w szkole, było tym wszystkim.
Gdzie zaczynamy

Wszystko zaczęło się na spotkaniu Krajowego Związku Nauczycieli. Równanie kwadratowe zostało przedstawione narodowi jako przykład okrutnych tortur zadawanych przez matematyków biednym, niczego nie podejrzewającym uczniom. Zaintrygowany tym oskarżeniem, równanie kwadratowe przyjęło główną rolę w najlepszym czasie antenowym, gdzie zostało przepytane przez groźnego ankietera, bardziej przyzwyczajonego do konfrontacji z premierem. Londyński „Times” zajął miejsce w swojej kolumnie liderów, zwykle zarezerwowanej dla poważnych dyskusji na temat moralnego (lub nie) zdrowia współczesnego świata, by ogłosić, że równanie kwadratowe jest bezużyteczne, matematyka jest bezużyteczna i że nikt nie chce się uczyć matematyki, więc po co się męczyć. Zaniepokojeni, aby niebezpieczne dopuszczenia przez równanie kwadratowe nie pozostały niepodważone, żywotne znaczenie równania dla przetrwania Wielkiej Brytanii było dyskutowane (pozytywny pogląd został przyjęty, możesz być zadowolony, aby wiedzieć) w brytyjskiej Izbie Gmin.
Gdzie by się to wszystko skończyło? Czy równanie kwadratowe było naprawdę martwe? Czy kogoś to obchodziło? Czy matematycy są naprawdę złymi potworami, którzy chcą tylko zadać równania kwadratowe młodszemu pokoleniu jako sposób na zepsucie ich nieśmiertelnych dusz?
Może tak, ale to nie jest tak naprawdę wina równania kwadratowego. W rzeczywistości, równanie kwadratowe odegrało kluczową rolę nie tylko w całej ludzkiej cywilizacji, jaką znamy, ale w możliwym wykrywaniu innych obcych cywilizacji, a nawet w tak istotnych współczesnych czynnościach jak oglądanie telewizji satelitarnej. Co jeszcze, poza naturą boskiego objawienia, można by uznać za mające taki wpływ na życie, jakie znamy? Rzeczywiście, w bardzo realnym sensie równania kwadratowe mogą uratować ci życie.
Babilończycy
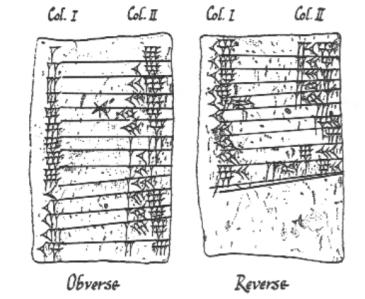
Babilońskie tabliczki z pismem klinowym zapisujące 9 tablic czasów
Wszystko zaczęło się około 3000 r. p.n.e. od Babilończyków. Byli oni jedną z pierwszych cywilizacji na świecie i wpadli na kilka wspaniałych pomysłów, takich jak rolnictwo, nawadnianie i pismo. Wyznaczali oni ścieżki Słońca, Księżyca i planet, a następnie zapisywali je na glinianych tabliczkach (które wciąż można oglądać w British Museum). Babilończykom zawdzięczamy współczesne idee kątów, w tym sposób, w jaki koło dzieli się na 360 stopni (dzięki małemu błędowi w obliczeniach, jeden na dzień). Babilończykom zawdzięczamy też raczej mniej przyjemny wynalazek (strasznego) podatnika. I to był jeden z powodów, dla których Babilończycy potrzebowali rozwiązywać równania kwadratowe.
Załóżmy, że jesteś babilońskim rolnikiem. Gdzieś na swojej farmie masz kwadratowe pole, na którym uprawiasz pewną roślinę. Jaką ilość swoich plonów możesz wyhodować na tym polu? Podwój długość każdego boku pola i okaże się, że możesz uprawiać cztery razy więcej plonów niż poprzednio. Powodem tego jest to, że ilość plonów, które możesz uprawiać jest proporcjonalna do powierzchni pola, która z kolei jest proporcjonalna do kwadratu długości boku. W kategoriach matematycznych, jeśli  jest długością boku pola,
jest długością boku pola, 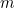 jest ilością plonów, które można uprawiać na kwadratowym polu o długości boku 1, a
jest ilością plonów, które można uprawiać na kwadratowym polu o długości boku 1, a  jest ilością plonów, które można uprawiać, wtedy
jest ilością plonów, które można uprawiać, wtedy
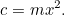 |
Oto nasze pierwsze równanie kwadratowe, nagie i mrugające w świetle słońca. Równania kwadratowe i obszary są ze sobą powiązane jak rodzeństwo w tej samej rodzinie. Jednak w tej chwili nie musimy niczego rozwiązywać – dopóki nie zjawi się pan podatnik! Wesoło mówi do rolnika „Chcę, abyś dał mi plonów, aby zapłacić za podatki z twojego gospodarstwa”. Rolnik ma teraz dylemat: jak dużego pola potrzebuje, aby wyhodować taką ilość plonów? Możemy łatwo odpowiedzieć na to pytanie, w rzeczywistości
plonów, aby zapłacić za podatki z twojego gospodarstwa”. Rolnik ma teraz dylemat: jak dużego pola potrzebuje, aby wyhodować taką ilość plonów? Możemy łatwo odpowiedzieć na to pytanie, w rzeczywistości
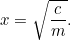 |
Znajdowanie pierwiastków kwadratowych za pomocą kalkulatora jest dla nas łatwe, ale stanowiło większy problem dla Babilończyków. W rzeczywistości opracowali oni metodę sukcesywnego przybliżania się do odpowiedzi, która jest identyczna z algorytmem (zwanym metodą Newtona-Raphsona) używanym przez współczesne komputery do rozwiązywania znacznie trudniejszych problemów niż równania kwadratowe.
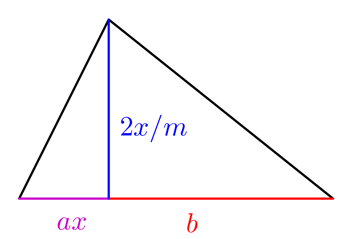
Nie wszystkie pola są kwadratowe. Załóżmy teraz, że rolnik ma pole o bardziej dziwnym kształcie z dwoma trójkątnymi sekcjami, jak pokazano po prawej stronie.
Dla odpowiednich wartości  i
i 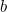 ilość plonów, które rolnik może uprawiać na tym polu, jest dana przez
ilość plonów, które rolnik może uprawiać na tym polu, jest dana przez
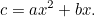 |
Wygląda to dużo bardziej jak równanie kwadratowe, do którego jesteśmy przyzwyczajeni, i nawet pod złym okiem podatnika, jest o wiele trudniejsze do rozwiązania. Jednak Babilończycy znów znaleźli odpowiedź. Najpierw podzielimy przez  , aby otrzymać
, aby otrzymać
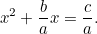 |
Teraz uzupełnimy kwadrat korzystając z faktu, że
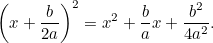 |
Łącząc to z oryginalnym równaniem, mamy
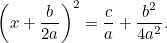 |
Jest to teraz równanie, które możemy rozwiązać, biorąc pierwiastki kwadratowe. Wynikiem jest słynny „wzór 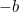 „:
„:
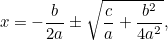 |
, który można zapisać jako.
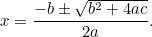 |
(We wzorze zwykle występuje „-4ac”, ponieważ równanie kwadratowe jest zwykle zapisywane w postaci „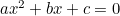 „.)
„.)
Fakt, że pierwiastek kwadratowy może dać pozytywną lub negatywną odpowiedź prowadzi do niezwykłego wyniku, że równanie kwadratowe ma dwa rozwiązania. To tyle, jeśli chodzi o zagadki matematyczne, które mają tylko jedno rozwiązanie!
Teraz, to jest miejsce, gdzie nauczanie równań kwadratowych często się kończy. Dotarliśmy do obiektu uwielbianego przez wszystkich dziennikarzy podczas wywiadów z matematykami – wzoru. Można wymyślać nieskończenie wiele pytań, które polegają na podstawieniu do wzoru wartości 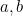 i
i  , aby uzyskać (dwie) odpowiedzi. Ale przecież nie o to chodzi w matematyce. Znalezienie wzoru to tylko pierwszy krok na długiej drodze. Musimy zapytać, co oznacza ta formuła; co mówi nam o wszechświecie; czy posiadanie formuły naprawdę ma znaczenie? Zobaczmy teraz, dokąd zaprowadzi nas ta formuła.
, aby uzyskać (dwie) odpowiedzi. Ale przecież nie o to chodzi w matematyce. Znalezienie wzoru to tylko pierwszy krok na długiej drodze. Musimy zapytać, co oznacza ta formuła; co mówi nam o wszechświecie; czy posiadanie formuły naprawdę ma znaczenie? Zobaczmy teraz, dokąd zaprowadzi nas ta formuła.
Niespodzianka dla Greków, odrobina matematycznego origami i wyczucie proporcji
Przedzielimy teraz 1000 lat do starożytnych Greków i zobaczymy, co zrobili z równaniami kwadratowymi. Grecy byli znakomitymi matematykami i odkryli wiele z matematyki, z której korzystamy do dziś. Jednym z równań, których rozwiązaniem byli zainteresowani, było (proste) równanie kwadratowe
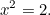 |

Wiedzieli, że to równanie ma rozwiązanie. W rzeczywistości jest to długość przeciwprostokątnej trójkąta prostokątnego, który miał boki długości jeden.
Z twierdzenia Pitagorasa wynika, że jeśli trójkąt prostokątny ma krótsze boki niż trójkąt różnoboczny, to jest to długość hipotensji.trójkąt prostokątny ma krótsze boki  i
i  oraz przeciwprostokątną
oraz przeciwprostokątną  to
to
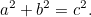 |
Podstawiając 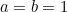 i
i  to
to 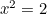 . Zatem
. Zatem 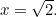
Czym więc jest  w tym przypadku? Lub, aby zadać pytanie, że Grecy zapytał, jaki rodzaj liczby jest to? Powód, że to miało znaczenie leżał w greckim poczuciu proporcji. Wierzyli oni, że wszystkie liczby są proporcjonalne względem siebie. Dokładniej mówiąc, oznaczało to, że wszystkie liczby były ułamkami postaci
w tym przypadku? Lub, aby zadać pytanie, że Grecy zapytał, jaki rodzaj liczby jest to? Powód, że to miało znaczenie leżał w greckim poczuciu proporcji. Wierzyli oni, że wszystkie liczby są proporcjonalne względem siebie. Dokładniej mówiąc, oznaczało to, że wszystkie liczby były ułamkami postaci 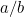 , gdzie
, gdzie  i
i  są liczbami całkowitymi. Liczby takie jak 1/2, 3/4 i 355/113 są przykładami ułamków. Naturalnym było oczekiwanie, że
są liczbami całkowitymi. Liczby takie jak 1/2, 3/4 i 355/113 są przykładami ułamków. Naturalnym było oczekiwanie, że  również jest ułamkiem. Ogromnym zaskoczeniem było to, że tak nie jest. W rzeczywistości
również jest ułamkiem. Ogromnym zaskoczeniem było to, że tak nie jest. W rzeczywistości
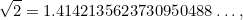 |
, gdzie kropki  oznaczają, że rozwinięcie dziesiętne
oznaczają, że rozwinięcie dziesiętne  trwa do nieskończoności bez żadnego dostrzegalnego wzoru. (Spotkamy się z tą sytuacją ponownie później, kiedy będziemy uczyć się o chaosie.)
trwa do nieskończoności bez żadnego dostrzegalnego wzoru. (Spotkamy się z tą sytuacją ponownie później, kiedy będziemy uczyć się o chaosie.)
 była pierwszą liczbą irracjonalną (to jest liczbą, która nie jest ułamkiem lub racjonalną), która została uznana za taką. Inne przykłady to
była pierwszą liczbą irracjonalną (to jest liczbą, która nie jest ułamkiem lub racjonalną), która została uznana za taką. Inne przykłady to 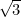 ,
, 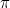 ,
,  i w rzeczywistości „większość” liczb. Zajęło to aż do 19 wieku, zanim mieliśmy dobry sposób myślenia o tych liczbach. Odkrycie, że
i w rzeczywistości „większość” liczb. Zajęło to aż do 19 wieku, zanim mieliśmy dobry sposób myślenia o tych liczbach. Odkrycie, że  nie jest liczbą racjonalną, wywołało zarówno wielkie podniecenie (100 wołów zostało złożonych w ofierze), jak i wielki szok, a odkrywca musiał popełnić samobójstwo. (Niech to będzie straszne ostrzeżenie dla zapalonych matematyków!) W tym momencie Grecy porzucili algebrę i zwrócili się ku geometrii.
nie jest liczbą racjonalną, wywołało zarówno wielkie podniecenie (100 wołów zostało złożonych w ofierze), jak i wielki szok, a odkrywca musiał popełnić samobójstwo. (Niech to będzie straszne ostrzeżenie dla zapalonych matematyków!) W tym momencie Grecy porzucili algebrę i zwrócili się ku geometrii.
Daleko od bycia niejasną liczbą, spotykamy  regularnie: za każdym razem, gdy używamy kartki papieru A4. W Europie rozmiary papieru mierzy się rozmiarami A, przy czym A0 jest największy, a jego powierzchnia wynosi
regularnie: za każdym razem, gdy używamy kartki papieru A4. W Europie rozmiary papieru mierzy się rozmiarami A, przy czym A0 jest największy, a jego powierzchnia wynosi 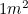 . Rozmiary A mają między sobą specjalną zależność. Jeśli teraz zrobimy trochę origami, biorąc kartkę papieru A1, a następnie składając ją na pół (wzdłuż jej najdłuższego boku), otrzymamy papier A2. Składając go ponownie na pół otrzymamy A3, a następnie A4 itd. Jednak papier jest tak zaprojektowany, że proporcje każdego z rozmiarów A są takie same – czyli każda kartka ma taki sam kształt.
. Rozmiary A mają między sobą specjalną zależność. Jeśli teraz zrobimy trochę origami, biorąc kartkę papieru A1, a następnie składając ją na pół (wzdłuż jej najdłuższego boku), otrzymamy papier A2. Składając go ponownie na pół otrzymamy A3, a następnie A4 itd. Jednak papier jest tak zaprojektowany, że proporcje każdego z rozmiarów A są takie same – czyli każda kartka ma taki sam kształt.
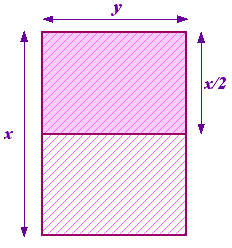
Możemy postawić pytanie, jaka to jest proporcja. Zacznijmy od kartki papieru o bokach x i y, gdzie x jest najdłuższym bokiem. Teraz dzielimy ją na dwie części, aby otrzymać kolejną kartkę o bokach y i x/2, przy czym y jest teraz najdłuższym bokiem. To jest pokazane po prawej stronie.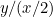 lub
lub 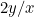 . Chcemy, aby te dwie proporcje były równe. Oznacza to, że
. Chcemy, aby te dwie proporcje były równe. Oznacza to, że
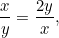 |
lub
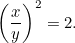 |
Kolejne równanie kwadratowe! Na szczęście jest to równanie, z którym już się spotkaliśmy. Rozwiązując je, stwierdzamy, że
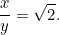 |
Ten wynik możesz łatwo sprawdzić. Wystarczy wziąć kartkę papieru formatu A4 (lub A3 czy A5) i zmierzyć boki. Możemy również obliczyć rozmiar każdego arkusza. Pole 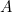 kartki papieru A0 jest dane przez
kartki papieru A0 jest dane przez
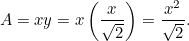 |
Ale wiemy, że 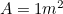 więc mamy kolejne równanie kwadratowe dla najdłuższego boku
więc mamy kolejne równanie kwadratowe dla najdłuższego boku  kartki A0, dane przez
kartki A0, dane przez
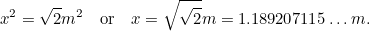 |
Oznacza to, że najdłuższy bok A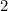 jest dany przez
jest dany przez 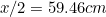 (dlaczego?), a A
(dlaczego?), a A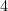 przez
przez 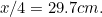 . Sprawdź to na własnych kartkach papieru.
. Sprawdź to na własnych kartkach papieru.
Papier używany w Stanach Zjednoczonych, zwany foolscap, ma inne proporcje. Aby zobaczyć dlaczego, wracamy do Greków i kolejnego równania kwadratowego. Wywoławszy taki żal, równanie kwadratowe odkupiło się w poszukiwaniu idealnych proporcji: poszukiwaniu, które trwa do dziś w projektowaniu planów filmowych i jest widoczne w wielu aspektach natury.
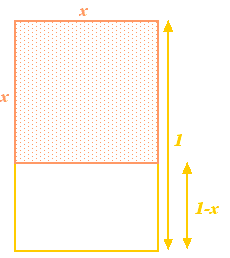
Zacznijmy od prostokąta, a następnie usuńmy z niego kwadrat o tej samej długości boku, co najkrótszy bok prostokąta. Jeśli najdłuższy bok prostokąta ma długość 1, a najkrótszy bok ma długość  , to kwadrat ma boki długości
, to kwadrat ma boki długości  . Usuwając go z prostokąta otrzymujemy mniejszy prostokąt o najdłuższym boku
. Usuwając go z prostokąta otrzymujemy mniejszy prostokąt o najdłuższym boku  i najmniejszym boku
i najmniejszym boku 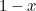 . Jak dotąd, abstrakcyjne. Grecy uważali jednak, że najbardziej estetyczny prostokąt (tzw. Złoty Prostokąt) to taki, dla którego skonstruowane powyżej duży i mały prostokąt mają takie same proporcje. Aby to było możliwe, musimy mieć
. Jak dotąd, abstrakcyjne. Grecy uważali jednak, że najbardziej estetyczny prostokąt (tzw. Złoty Prostokąt) to taki, dla którego skonstruowane powyżej duży i mały prostokąt mają takie same proporcje. Aby to było możliwe, musimy mieć
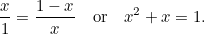 |
Jest to kolejne równanie kwadratowe: bardzo ważne, które pojawia się we wszystkich możliwych zastosowaniach. Ma ono (dodatnie) rozwiązanie
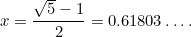 |
Liczba  jest nazywana złotą proporcją i jest często oznaczana grecką literą
jest nazywana złotą proporcją i jest często oznaczana grecką literą 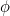 .
.

Złoty prostokąt można dostrzec w kształcie okien, zwłaszcza w domach georgiańskich. Ostatnio Złoty Prostokąt można również znaleźć jako „idealny kształt” dla fotografii i obrazów filmowych. Równanie kwadratowe 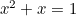 pojawia się również w badaniach populacji królików oraz we wzorze, w jakim ułożone są nasiona słonecznika i liście na łodygach roślin. Wszystkie te elementy są powiązane ze złotą proporcją poprzez ciąg Fibonacciego, który ma postać
pojawia się również w badaniach populacji królików oraz we wzorze, w jakim ułożone są nasiona słonecznika i liście na łodygach roślin. Wszystkie te elementy są powiązane ze złotą proporcją poprzez ciąg Fibonacciego, który ma postać
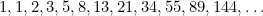 |

Nasiona słonecznika, ułożone za pomocą liczb Fibonacciego |
Partenon, ucieleśniający złotą proporcję |
W tym ciągu każdy człon jest sumą dwóch poprzednich członów. Fibonacci odkrył go w XV wieku, próbując przewidzieć przyszłą populację królików. Jeśli weźmiemy pod uwagę stosunek każdego terminu do następnego, otrzymamy ciąg liczb
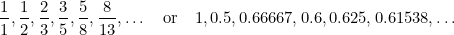 |
, a liczby te coraz bardziej zbliżają się do (zgadłeś) złotego podziału 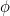 .
.
Znajdując oba pierwiastki powyższego równania kwadratowego, możemy znaleźć wzór na n-ty człon ciągu Fibonacciego. Jeśli  jest
jest 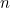 tą taką liczbą z
tą taką liczbą z 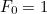 i
i 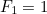 to
to  jest dana wzorem
jest dana wzorem
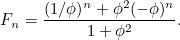 |
Koniki łączą równania kwadratowe z gwiazdami

Grecy byli również bardzo zainteresowani kształtem stożków. Rysunek po lewej stronie przedstawia typowy stożek.
Połowa stożka może być wyobrażona jako rozprzestrzenianie się światła pochodzącego z pochodni. Jeśli zaświecimy latarką na płaską powierzchnię, taką jak ściana, zobaczymy różne kształty, gdy będziemy poruszać latarką. Kształty te nazywamy przekrojami stożkowymi i są to krzywe, które otrzymamy, jeśli przekrój przez stożek wykonamy pod różnymi kątami. Dokładnie te krzywe były badane przez Greków i uznali oni, że istnieją zasadniczo cztery rodzaje przekrojów stożkowych. Jeśli weźmiemy przekrój poziomy przez stożek, otrzymamy okrąg. Przekrój pod małym kątem do poziomu daje elipsę. Jeśli weźmiemy odcinek pionowy, to otrzymamy hiperbolę, a jeśli weźmiemy odcinek równoległy do jednego boku stożka, to otrzymamy parabolę. Krzywe te są zilustrowane poniżej.
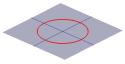




Przekrój poprzecznyprzekrojem stożka może być okrąg …

… elipsa …
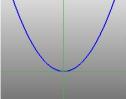
… parabola …
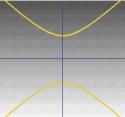
…. lub hiperbola.
Odcinki kanoniczne pojawiają się w naszej historii, ponieważ każdy z nich jest opisany przez równanie kwadratowe. W szczególności, jeśli 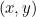 reprezentuje punkt na każdej krzywej, to równanie kwadratowe łączy
reprezentuje punkt na każdej krzywej, to równanie kwadratowe łączy  i
i 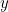 . Mamy:
. Mamy:
Krąg: 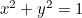 ;
;
Elipsa: 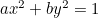 ;
;
Hiperbolę: 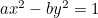 ;
;
Parabola: 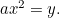
Krzywe te były znane i badane od czasów Greków, ale poza okręgiem nie wydawały się mieć żadnego praktycznego zastosowania. Jednak, jak zobaczymy w następnym numerze Plusa, związek między równaniami kwadratowymi i stożkowymi, w połączeniu z ogromnym szczęśliwym trafem, doprowadził do zrozumienia sposobu, w jaki działa wszechświat, a w XVI wieku nadszedł czas, by stożkowe zmieniły świat.
O autorach
Chris Budd jest profesorem matematyki stosowanej w Departamencie Nauk Matematycznych na Uniwersytecie w Bath oraz Katedrą Matematyki w Royal Institution w Londynie.
Chris Sangwin jest pracownikiem Szkoły Matematyki i Statystyki na Uniwersytecie w Birmingham. Jest Research Fellow w centrum Learning and Teaching Support Network dla Mathematics, Statistics, and Operational Research.
Oni ostatnio napisali popularną książkę Mathematics Galore!, wydaną przez Oxford University Press.
Ten artykuł został zainspirowany częściowo przez niezwykłą debatę w brytyjskiej Izbie Gmin na temat równań kwadratowych. Zapis tej debaty można znaleźć w Hansard, United Kingdom House of Commons, 26 June 2003, Columns 1259-1269, 2003, który jest dostępny online na stronie House of Commons Hansard Debate.
.