Zero

Lo zero è il numero intero indicato con 0 che, se usato come numero di conteggio, significa che non ci sono oggetti. È l’unico numero intero (e, di fatto, l’unico numero reale) che non è né negativo né positivo. Un numero che non è zero è detto non zero. Una radice di una funzione è anche conosciuta a volte come “uno zero di .”

Il segmento di Schoolhouse Rock “My Hero, Zero” esalta le virtù dello zero con lodi come: “Il mio eroe, zero Un piccolo eroe divertente Ma fino a quando sei arrivato tu abbiamo contato sulle nostre dita delle mani e dei piedi Ora sei qui per rimanere E nessuno sa davvero quanto sei meraviglioso Perché non potremmo mai raggiungere una stella senza di te, zero, mio eroe Quanto sei meraviglioso.”

Zero è comunemente preso per avere la fattorizzazione (ad es, nel comando FactorInteger del linguaggio Wolfram). D’altra parte, i divisori e la funzione divisore sono generalmente considerati indefiniti, poiché per convenzione, (cioè, divide 0) per ogni tranne zero.

Poiché il numero di permutazioni di elementi 0 è 1, (fattoriale dello zero) è definito come 1 (Wells 1986, p. 31). Questa definizione è utile per esprimere molte identità matematiche in forma semplice.

Un numero diverso da 0 portato alla potenza 0 è definito come 1, che segue dal limite

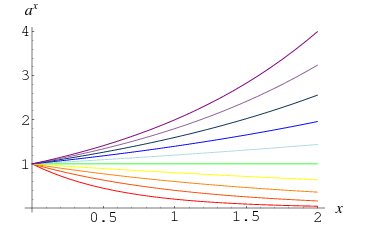
Questo fatto è illustrato dalla convergenza delle curve a nel grafico sopra, che mostra per , 0.4, …, 2.0. Può anche essere visto più intuitivamente notando che prendere ripetutamente la radice quadrata di un numero dà numeri sempre più piccoli che si avvicinano a uno dall’alto, mentre fare lo stesso con un numero tra 0 e 1 dà numeri sempre più grandi che si avvicinano a uno dal basso. Per radici quadrate, la potenza totale presa è , che si avvicina a 0 come è grande, dando nel limite che è grande.

stesso è indefinito. La mancanza di un significato ben definito per questa quantità segue dai fatti reciprocamente contraddittori che è sempre 1, quindi dovrebbe essere uguale a 1, ma è sempre 0 (per ), quindi dovrebbe essere uguale a 0. Si potrebbe sostenere che è una definizione naturale poiché

Tuttavia, il limite non esiste per valori complessi generali di . Pertanto, la scelta della definizione per è solitamente definita come indeterminata.

Tuttavia, la definizione di permette di esprimere semplicemente alcune formule (Knuth 1992; Knuth 1997, p. 57), di cui un esempio è la bella formula analitica per l’integrale della funzione sinc generalizzata

data da Kogan (cfr. Espinosa e Moll 2000), dove , , e è la funzione floor.

Il teorema di Richardson è un risultato fondamentale nella teoria della decidibilità che stabilisce che la determinazione se anche semplici espressioni sono identicamente uguali a zero è indecidibile in linea di principio, figuriamoci nella pratica.

La seguente tabella fornisce i primi numeri tali che l’espansione decimale di non contenga zeri per piccoli (un problema che assomiglia alla questione di Gelfand). Il più grande conosciuto per cui non contiene zeri è 86 (Madachy 1979), con nessun altro (M. Cook, pers. comm, 26 settembre 1997 e 16 marzo 1998), migliorando il limite ottenuto da Beeler e Gosper (1972). I valori tali che le posizioni dello zero più a destra in aumentano sono 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, … (OEIS A031140). Le posizioni in cui si trovano gli zeri più a destra sono 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, … (OEIS A031141). Lo zero più a destra di si trova alla 217a posizione decimale, la più lontana per le potenze fino a .

	Sloane	tale che non contiene 0
2	A007377	1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, …
3	A030700	1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, …
4	A030701	1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, …
5	A008839	1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, …
6	A030702	1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, …
7	A030703	1, 2, 3, 6, 7, 10, 11, 19, 35
8	A030704	1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24 27
9	A030705	1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34
11	A030706	1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, …

Sebbene non sia stato dimostrato che i numeri elencati sopra siano gli unici senza zeri per una data base, la probabilità che ne esistano altri è molto bassa. Sotto questa ipotesi, la sequenza dei più grandi tali che non contiene zeri per , 3, … è quindi data da 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, … (OEIS A020665).