A nulla a 0-val jelölt egész szám, amely számlálószámként használva azt jelenti, hogy nincsenek objektumok. Ez az egyetlen olyan egész szám (és valójában az egyetlen valós szám), amely nem negatív és nem pozitív. Az olyan számot, amely nem nulla, nem nullának nevezzük. Egy 
függvény gyökét néha úgy is nevezik, hogy “a 
nullája.”
A Schoolhouse Rock “My Hero, Zero” című szegmense a nulla erényeit dicséri olyan dicséretekkel, mint: “My hero, zero Such a funny little hero But until you came along We counted on our fingers and toes Now you’re here to stay And nobody really knows How wonderful you are Why we could never reach a star Without you, zero, my hero How wonderful you are.”
A nullát általában a 
faktorizációval veszik fel (pl, a Wolfram Language FactorInteger parancsában). Másrészt az osztókat és a 
osztófüggvényt általában meghatározatlannak veszik, mivel a konvenció szerint 
(azaz 
osztja a 0-t) minden 
esetében, kivéve a nullát.”
Mert mivel a 0 elemek permutációinak száma 1, a 
(nulla faktoriális) definíciója 1 (Wells 1986, 31. o.). Ez a definíció sok matematikai azonosság egyszerű formában történő kifejezésére alkalmas.
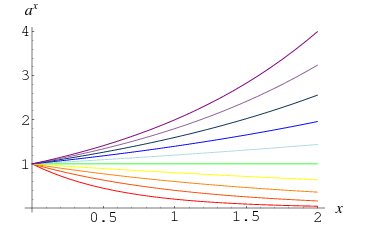
A 0-tól eltérő, 0 hatványra vett számot 1-nek definiáljuk, ami a
 |
(1)
|
Ezt a tényt a fenti ábrán a görbék 
-nál való konvergenciája szemlélteti, amely 
, 0 esetén 
-ot mutat.4, …, 2.0. Ez intuitívabban is belátható, ha megfigyeljük, hogy egy 
szám négyzetgyökének ismételt kivonása egyre kisebb és kisebb számokat ad, amelyek felülről közelítenek az egyhez, míg ha ugyanezt egy 0 és 1 közötti számmal tesszük, akkor egyre nagyobb és nagyobb számokat kapunk, amelyek alulról közelítenek az egyhez. A 
négyzetgyök esetében az összes vett hatvány 
, amely a 0-hoz közelít, ahogy 
nagy, és 
-ot ad abban a határértékben, hogy 
nagy.
önmagában meghatározhatatlan. E mennyiség jól definiált jelentésének hiánya abból az egymásnak ellentmondó tényből következik, hogy 
mindig 1, tehát 
-nek 1-nek kell lennie, de 
mindig 0 (
esetén), tehát 
-nak 0-nak kell lennie. Lehetne azzal érvelni, hogy 
egy természetes definíció, mivel
 |
(2)
|
A határérték azonban nem létezik 
általános komplex értékeire. Ezért a 
definíciójának megválasztását általában határozatlannak határozzák meg.
Az 
definiálása azonban lehetővé teszi, hogy egyes képletek egyszerűen kifejezhetőek legyenek (Knuth 1992; Knuth 1997, p. 57), amire példa az általánosított sinc függvény
 |
(3)
|
által adott gyönyörű analitikus formula, ahol 
, 
és 
a padlófüggvény , és .
Richardson tétele a eldönthetőségelmélet egyik alapvető eredménye, amely megállapítja, hogy annak meghatározása, hogy akár egyszerű kifejezések is azonosan egyenlők-e nullával, elvileg eldönthetetlen, nemhogy a gyakorlatban.
A következő táblázat megadja az első néhány olyan 
számot, amelyeknél a 
tizedesvégi bővítménye kis 
esetén nem tartalmaz nullát (ez a probléma hasonlít Gelfand kérdésére.) A legnagyobb ismert 
, amelynél a 
nem tartalmaz nullát, 86 (Madachy 1979), más 
nincs (M. Cook, pers. comm.., Sep. 26, 1997 és Mar. 16, 1998), ami javítja a Beeler és Gosper (1972) által kapott 
határértéket. Az olyan 
értékek, amelyeknél a 
jobb szélső nullájának pozíciója növekszik, a következők: 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, … (OEIS A031140). A jobb szélső nullák a következő pozíciókban fordulnak elő: 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, …. (OEIS A031141). Az 
jobb oldali nullája a 217. tizedesjegyen áll, ami a legtávolabbi a 
-ig terjedő hatványoknál.
 |
Sloane |  olyan, hogy  nem tartalmaz 0-t |
| 2 | A007377 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, … |
| 3 | A030700 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, … |
| 4 | A030701 | 1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, … |
| 5 | A008839 | 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, … |
| 6 | A030702 | 1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, … |
| 7 | A030703 | 1, 2, 3, 6, 7, 10, 11, 19, 35 |
| 8 | A030704 | 1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24, 27 |
| 9 | A030705 | 1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34 |
| 11 | A030706 | 1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, … |
Noha nem bizonyított, hogy a fent felsorolt számok az egyetlenek, amelyek nem tartalmaznak nullát az adott bázison, annak a valószínűsége, hogy további számok léteznek, eltűnően kicsi. E feltételezés mellett a legnagyobb 
olyan sorozata, hogy 
nem tartalmaz nullát 
, 3, … esetén a következő: 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, …. (OEIS A020665).