Les différents types de contrôleurs sont utilisés pour améliorer les performances des systèmes de contrôle. Dans ce chapitre, nous aborderons les contrôleurs de base tels que le contrôleur proportionnel, le contrôleur dérivé et le contrôleur intégral.
Contrôleur proportionnel
Le contrôleur proportionnel produit une sortie, qui est proportionnelle au signal d’erreur.
$$u(t) \propto e(t) $$
$$\Rightarrow u(t)=K_P e(t)$$
Appliquez la transformée de Laplace sur les deux côtés -.
$U(s)=K_P E(s)$$
$$\frac{U(s)}{E(s)}=K_P$$
Donc, la fonction de transfert du régulateur proportionnel est $K_P$.
Où,
U(s) est la transformée de Laplace du signal d’actionnement u(t)
E(s) est la transformée de Laplace du signal d’erreur e(t)
KP est la constante de proportionnalité
Le schéma fonctionnel du système de commande en boucle fermée à rétroaction négative unitaire avec le régulateur proportionnel est présenté dans la figure suivante.
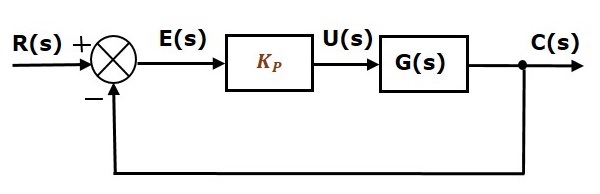
Le contrôleur proportionnel est utilisé pour changer la réponse transitoire selon les besoins.
Contrôleur dérivatif
Le contrôleur dérivatif produit une sortie, qui est la dérivée du signal d’erreur.
$u(t)=K_D \frac{\text{d}e(t)}{\text{d}t}$
Appliquez la transformée de Laplace sur les deux côtés.
$U(s)=K_D sE(s)$$
$$\frac{U(s)}{E(s)}=K_D s$
Donc, la fonction de transfert du contrôleur dérivé est $K_D s$.
Où, $K_D$ est la constante de dérivation.
Le schéma fonctionnel du système de commande en boucle fermée à rétroaction négative unitaire avec le contrôleur dérivé est présenté dans la figure suivante.
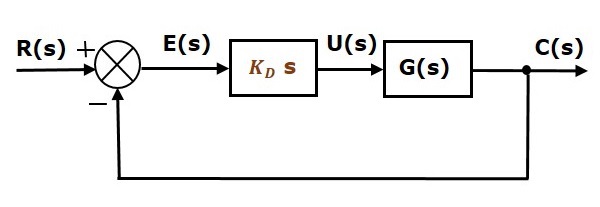
Le contrôleur dérivé est utilisé pour transformer le système de commande instable en un système stable.
Contrôleur intégral
Le contrôleur intégral produit une sortie, qui est intégrale du signal d’erreur.
$$u(t)=K_I \int e(t) dt$$
Appliquer la transformée de Laplace sur les deux côtés –
$U(s)=\frac{K_I E(s)}{s}$
$$\frac{U(s)}{E(s)}=\frac{K_I}{s}$
Donc, la fonction de transfert du contrôleur intégral est $\frac{K_I}{s}$.
Où, $K_I$ est la constante intégrale.
Le schéma fonctionnel du système de commande en boucle fermée à rétroaction négative unitaire avec le contrôleur intégral est présenté dans la figure suivante.
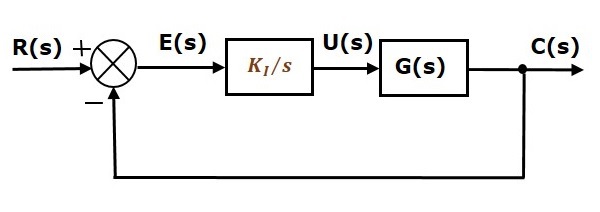
Le contrôleur intégral est utilisé pour diminuer l’erreur en régime permanent.
Discutons maintenant de la combinaison des contrôleurs de base.
Contrôleur proportionnel dérivé (PD)
Le contrôleur proportionnel dérivé produit une sortie, qui est la combinaison des sorties des contrôleurs proportionnel et dérivé.
$$u(t)=K_P e(t)+K_D \frac{\text{d}e(t)}{\text{d}t}$
Appliquez la transformée de Laplace sur les deux côtés -.
$U(s)=(K_P+K_D s)E(s)$$
$$\frac{U(s)}{E(s)}=K_P+K_D s$$
Donc, la fonction de transfert du contrôleur proportionnel dérivé est $K_P + K_D s$.
Le schéma fonctionnel du système de commande en boucle fermée à rétroaction négative unitaire avec le contrôleur proportionnel dérivé est présenté dans la figure suivante.
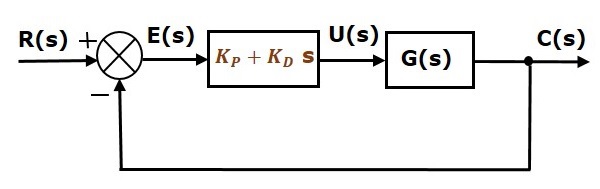
Le contrôleur proportionnel dérivé est utilisé pour améliorer la stabilité du système de commande sans affecter l’erreur de régime permanent.
Contrôleur proportionnel intégral (PI)
Le contrôleur proportionnel intégral produit une sortie, qui est la combinaison des sorties des contrôleurs proportionnel et intégral.
$u(t)=K_P e(t)+K_I \int e(t) dt$$
Appliquez la transformée de Laplace sur les deux côtés -.
$U(s)=\left(K_P+\frac{K_I}{s} \right )E(s)$$
$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}$
Donc, la fonction de transfert du régulateur proportionnel intégral est $K_P + \frac{K_I} {s}$.
Le schéma fonctionnel du système de commande en boucle fermée à rétroaction négative unitaire avec le contrôleur proportionnel intégral est présenté dans la figure suivante.
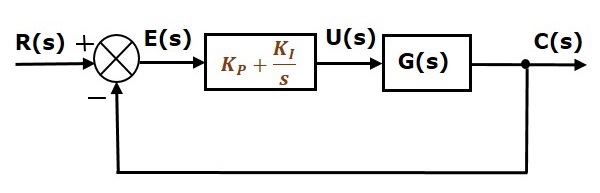
Le contrôleur proportionnel intégral est utilisé pour diminuer l’erreur en régime permanent sans affecter la stabilité du système de commande.
Contrôleur proportionnel intégral dérivé (PID)
Le contrôleur proportionnel intégral dérivé produit une sortie, qui est la combinaison des sorties des contrôleurs proportionnel, intégral et dérivé.
$u(t)=K_P e(t)+K_I \int e(t) dt+K_D \frac{\text{d}e(t)}{\text{d}t}$
Appliquez la transformée de Laplace sur les deux côtés -.
$U(s)=\left(K_P+\frac{K_I}{s}+K_D s \right )E(s)$$
$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}+K_D s$$
Donc, la fonction de transfert du régulateur proportionnel intégral dérivé est $K_P + \frac{K_I} {s} + K_D s$.
Le schéma fonctionnel du système de commande en boucle fermée à rétroaction négative unitaire avec le contrôleur dérivé intégral proportionnel est présenté dans la figure suivante.
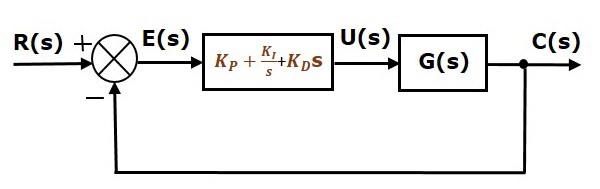
Le contrôleur dérivé intégral proportionnel est utilisé pour améliorer la stabilité du système de commande et pour diminuer l’erreur en régime permanent.
.