L’angle fait lorsque le rayon
est enroulé autour du cercle:
 |
1 Radian fait environ 57,2958 degrés. |
Pourquoi « 57,2958… » degrés ? Nous allons le voir dans un instant.
Le Radian est une mesure pure basée sur le Rayon du cercle:
Radian : l’angle fait quand on prend le rayon
et qu’on l’enroule autour du cercle.
Radians et degrés
Voyons pourquoi 1 Radian est égal à 57.2958… degrés:
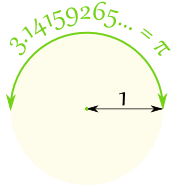
Dans un demi-cercle, il y aπ radians, qui est aussi 180°
Pour passer des radians aux degrés : multiplier par 180, diviser par π
Pour passer des degrés aux radians : multiplier par π, diviser par 180
Voici un tableau des valeurs équivalentes :
| Degrees | Radians (exact) |
Radians (approx) |
|---|---|---|
| 30° | π/6 | 0.524 |
| 45° | π/4 | 0,785 |
| 60° | π/3 | 1.047 |
| 90° | π/2 | 1,571 |
| 180° | π | 3.142 |
| 270° | 3π/2 | 4,712 |
| 360° | 2π | 6,283 |
Exemple : Combien de radians dans un cercle complet ?
Imaginez que vous coupez des morceaux de ficelle de la longueur exacte du centre à la circonférence d’un cercle….
… combien de morceaux avez-vous besoin pour faire une fois le tour du cercle ?
Réponse : 2π (ou environ 6,283 morceaux de ficelle).
Radians préférés des mathématiciens
Parce que le radian est basé sur l’idée pure que « le rayon est posé le long de la circonférence », il donne souvent des résultats simples et naturels lorsqu’il est utilisé en mathématiques.
Par exemple, regardez la fonction sinus pour de très petites valeurs :

