Une question importante est de savoir comment les nombres premiers sont distribués parmi les entiers. La réponse est, en très peu de mots, plutôt au hasard, étant donné certaines statistiques de base….
 Bill Casselman
Bill Casselman
Université de la Colombie-Britannique, Vancouver, Canada
Email Bill Casselman
| |
|
Introduction
Il y a plusieurs années, on a conjecturé qu’il existait un nombre infini de paires de nombres premiers $p$, $q$ avec $q = p+2$. Il y a eu quelques progrès récents (et célèbres) sur ce problème. Je ne parlerai pas des progrès récents, mais plutôt de ce que nous attendons – plutôt que de ce que nous savons – de ces paires. Rien de ce que je dirai n’est nouveau, et je n’ai fait, dans une certaine mesure, que développer ce que Andrew Granville dit dans sa récente note d’exposition sur les progrès récents.
Combien de nombres premiers attendons-nous ?
Un nombre premier est un entier positif qui n’a pas de diviseurs sauf lui-même et $1$. La définition est simple, mais dès que l’on commence à explorer la signification des nombres premiers, on se rend compte qu’ils présentent un comportement beaucoup plus subtil. Une question importante est la suivante : comment les nombres premiers sont-ils répartis parmi les nombres entiers ? La réponse est, en très peu de mots, plutôt aléatoire, compte tenu de certaines statistiques de base. Qu’est-ce que je veux dire par là ?
Bien, voici un tableau carré représentant tous les nombres premiers jusqu’à 400$:

Il y a quelques modèles dans ce tableau, dont certains que je commenterai plus tard. La plupart de ceux que vous percevez sont causés par un artefact de l’affichage. Par exemple, une colonne sur deux est essentiellement vide, et ce parce que le seul nombre premier pair est $2$. De même, une colonne sur cinq est essentiellement vide. Les paires de nombres premiers jumeaux sont plus intéressantes (certaines d’entre elles ne sont pas aussi visibles car elles sont divisées en deux rangées, comme $59$, $61$), ainsi que certains modèles liés aux derniers chiffres affichés. Ce sont ce que l’on pourrait appeler des motifs locaux. Il n’y en a pas de globaux apparents.
On a fait beaucoup d’efforts pour trouver des moyens extrêmement efficaces de produire des nombres premiers, mais de nos jours, même un programme très simple ne prend que peu de temps pour faire de grandes listes de nombres premiers. L’un des programmes les plus fructueux fera une grande liste de nombres premiers et l’utilisera ensuite pour calculer la fonction $\pi(n)$, le nombre de nombres premiers $\le n$.
Une chose à laquelle cela peut servir est d’avoir une idée approximative de la fréquence des nombres premiers. Il y a $135$ de nombres premiers dans l’intervalle $$:
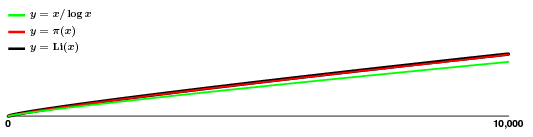
L’approximation semble excellente ! Donc, même si $\pi(x)$ rebondit un peu, apparemment sans grand motif, nous en avons une assez bonne estimation, ce qui signifie que nous avons une bonne idée de la façon dont les nombres premiers croissent, au moins en moyenne.
Il faut cependant garder à l’esprit que l’apparente douceur est trompeuse. De près, voici à quoi ressemblent les deux courbes supérieures :

Commentaires?
Raisonnement heuristique sur les nombres premiers jumeaux
Les nombres premiers jumeaux sont une paire $p$, $p+2$ qui sont tous deux des nombres premiers. Par exemple, à partir d’un des tracés ci-dessus, on voit les nombres premiers jumeaux $$, , , , , $$
et d’autres. On a conjecturé qu’il y en a un nombre infini, mais bien qu’il y ait beaucoup de preuves empiriques pour cela, cela n’a pas encore été prouvé.
Peut-être que la preuve la plus forte est une formule qui approche le nombre $\pi_{2}(x)$ de nombres premiers jumeaux $\le x$ remarquablement bien. Je ne suis pas tout à fait sûr de l’origine de cette formule, mais elle est apparue pour la première fois dans un article de G. H. Hardy et J. E. Littlewood (eux-mêmes une paire de nombres premiers jumeaux) daté de 1923. L’article contient plusieurs formules similaires, toutes basées sur la même méthode, qu’ils avaient utilisée pour résoudre de nombreux problèmes auparavant. Il s’agissait de leur méthode du cercle. Leur dérivation de la formule pour $\pi_{2}(x)$ n’est pas du tout rigoureuse, mais elle est très convaincante. Il y a un compte rendu succinct de cela dans une annexe de l’article d’Andrew Granville.
Mais juste après la Seconde Guerre mondiale, Lord Cherwell (Frederick Lindemann) a suggéré une dérivation probabiliste plus élémentaire (et toujours pas rigoureuse). Cela a conduit à une collaboration avec E. M. Wright et finalement à une publication conjointe posthume. Ceci est expliqué dans la section 22.20 du texte bien connu de Hardy et Wright. On en trouve également une version légèrement plus élémentaire dans une annexe de l’article de Granville (section 2.5). Je le suis.
Le point de départ du raisonnement plausible est notre estimation de $\pi(x)$, le nombre de nombres premiers inférieurs ou égaux à $x$. L’idée de base de la dérivation est que les nombres premiers sont, dans une bonne mesure, distribués aléatoirement. Nous savons qu’au voisinage de $x$ la densité des nombres premiers est d’environ $1/\log x$. Si les nombres premiers étaient distribués au hasard, la probabilité que deux nombres donnés proches de $x$ soient des nombres premiers ne serait alors que le produit des probabilités locales, soit $1/\log^{2} x$. Il s’agit certainement d’un raisonnement spécieux, puisque si $n > 2$ la probabilité que $n$ et $n+1$ soient tous deux des nombres premiers est de $0$, alors que le fait que $p$ soit un nombre premier semblerait augmenter les chances que $p+2$ le soit. Il y a des considérations similaires à prendre en compte en raison de la divisibilité possible par d’autres petits nombres premiers, aussi, au voisinage de $x$.
Il y a un fait simple dans cette histoire. Si $q$ est un nombre premier quelconque, alors la probabilité de choisir au hasard un entier qui n’est pas divisible par $q$ est de 1-1/q$. La probabilité d’en choisir deux qui ne sont pas divisibles par $q$ est donc le produit $(1 – 1/q)^{2}$. Supposons que $p$ et $p+2$ soient tous deux des nombres premiers, alors ni $p$ ni $p+2$ ne sont divisibles par $q$. Si $q$ = 2$, cela se produit dans 1/2$ des cas. Si $q \ne 2$, la probabilité que $p \not\equivaut à 0$ et $p \not\equivaut à -2$ modulo $q$ est $(1 – 2/q)$. En raison du théorème du reste du chinois, la divisibilité par deux nombres premiers est un événement indépendant. Ainsi, si $x$ est grand et que $Q$ est relativement petit, la probabilité que toute paire de nombres $m$ et $n$ proche de $x$ ne soit pas un multiple d’un nombre premier jusqu’à $Q$ est $$ { 1\over 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} } \. $$
Disons que $\Gamma_{Q}$ est le rapport de celui-ci à $\prod_{q \le Q}(1 – 2/q)$ : $$ \Gamma_{Q} = { 1\over 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} \over (1 – 2/q) } $$ Nous avons $$ { 1 – 2/q \over (1-1/q)^{2}} } = { (1 – 1/q)^{2} – 1/q^{2} \over (1 – 1/q)^{2} } = 1 – { 1 \over (q -1)^{2} } \, . $$ Un critère standard affirme que ce produit converge si la somme $\sum 1/(q-1)^{2}$ converge. Mais il converge bel et bien puisque le test de l’intégrale nous dit que $\sum 1/n^{2}$ converge. Par conséquent, ce produit converge en fait vers un nombre $\Pi_{\infty}$ lorsque $Q \rightarrow \infty$. Soit $C_{2}$ son inverse. La section 2.5 de l’article de Granville dit qu’il devrait être intuitivement raisonnable à ce stade que le nombre $\pi_{2}(x)$ de nombres premiers jumeaux $\le x$ soit approximé par $$ \Pi_{2}(x) = C_{2} \int_{2}^{\infty} {dx \over \log^{2} x } \. $$
Le texte de Hardy et Wright expose une analyse plus prudente qui rend le saut intuitif un peu plus clair.
La valeur de la constante ici a été calculée il y a longtemps par J. W. Wrench pour être d’environ 1$.32032363169373914785562422002911155686525 $. Voici une comparaison de quelques valeurs de $\pi_{2}(x)$ et de la formule dans l’intervalle $$ : $$ \matrix{ n & 10 000 & 20 000 & 30 000 & 40 000 & 50 000 \cr \pi_{2}(n) & 205\phantom{.0} & 342 \phantom{.0} & 467 \phantom{.0} & 591 \phantom{.0} & 705 \phantom{.0} & \cr \Pi_{2}(x) & 214.2 & 357.7 & 486.7 & 607.4 & 722.5 \cr } $$ $$ \matrix{ n & 60.000 & 70.000 & 80.000 & 90.000 & 100.000 \cr \pi_{2}(n) & 811 \phantom{.0} & 905 \phantom{.0} & 1007 \phantom{.0} & 1116 \phantom{.0} & 1224 \phantom{.0} \cr \Pi_{2}(x) & 833.3 & 940.9 & 1045.7 & 1148.2 & 1248.7 \cr } $$
Commentaires?
Conjecture de Dickson
Les nombres premiers jumeaux sont un cas particulier de quelque chose de bien plus général. On peut se demander s’il existe un nombre infini de paires $p$, $p+4$ ou $p$, $p+6$ qui sont des nombres premiers ? Ou encore $p$, $p+10$ ? Le cas de $p$ et $p+10$ est certainement suggéré par l’une des images ci-dessus, dans laquelle de telles paires sont facilement visibles. Que diriez-vous de triples quelconques ? Supposons que $a_{1}$, $a_{2}$, $\ldots$ , $a_{k}$ constituent un tableau d’entiers. Peut-on s’attendre à ce qu’il existe une infinité d’ensembles $n+a_{1}$, $n+a_{2}$, $\ldots$ , $n+a_{k}$ tous premiers ?
Il faut être un peu prudent. Il n’existe pas de couples premiers de la forme $p$, $p+1$ (passé $p = 2$), car l’un de ces deux nombres doit être divisible par 2$. De même, passé $p = 3$, il n’existe pas de triplets premiers $p$, $p+2$, $p+4$ car l’un d’entre eux doit être divisible par $3$.
Ce dernier exemple devrait être éclairant. Le nombre $p+4$ est divisible par $3$ si et seulement si $p+1$ est divisible par $3$. Donc $3$ divise un des nombres $p$, $p+2$, $p+4$ si et seulement s’il divise $p$, $p+1$, $p+2$. Mais ceci est sûr d’arriver, puisque le dernier triple couvre clairement tous les nombres modulo $3$.
En général, on dit que $p$ est une obstruction pour le tableau $(a_{i})$ si $p$ divise toujours au moins un de chaque séquence $n+a_{i}$ ($i = 1$, $\ldots$, $k$). Ceci se produit si et seulement si les nombres $a_{i} \ ; {\rm mod} \, p$ remplissent tout $Z/p$.
Cela ne peut jamais arriver si $p > k$, donc pour vérifier si un certain $p$ fait obstacle à $(a_{i})$ il suffit de vérifier si les $a_{i}$ couvrent $Z/p$ pour tout $p \le k$. On appelle le tableau $(a_{i})$ admissible s’il n’a pas d’obstructions premières.
Par exemple, $(1,3,7,9)$ est un tableau admissible, puisque, comme on peut le vérifier facilement, ni $2$ ni $3$ ne sont des obstructions. Plusieurs séquences premières correspondant à ce modèle peuvent être vues dans l’un des diagrammes ci-dessus. D’autres exemples sont (a) tout $0$, $2n$ ; (b) $0$, $4$, $6$ ; (c) $0$, $2$, $6$.
Il existe des ensembles admissibles arbitrairement grands. En effet :
Théorème. Si $a_{1}$ à $a_{k}$ est un ensemble quelconque de nombres premiers distincts $> k$, ils constituent un ensemble admissible.
Pourquoi ? Si $p$ est un nombre premier quelconque où $p> k$, alors nous avons déjà vu qu’il ne peut pas être une obstruction. Mais si $p \le k$, alors il ne peut diviser aucun des $a_{i}$, dont aucun ne peut être congru à $0$ modulo $p$. Donc les $a_{i}$ ne remplissent pas $Z/p$.
Un cas particulier d’une conjecture faite à l’origine par L. E. Dickson est que s’il n’y a pas d’obstructions premières à $(a_{i})$ alors il existe une infinité de suites premières de la forme $(n +a_{i})$.
Ce qui s’est passé récemment
Ce n’est pas le lieu pour raconter toute l’histoire, qui a été couverte de manière approfondie dans d’autres endroits. Je recommande particulièrement l’article de Quanta par Erica Klarreich pour un compte rendu populaire, et l’essai de Granville pour un compte rendu plus technique. Je veux juste énoncer un peu plus précisément que dans le récit de Klarreich ce qu’est le plus célèbre des nouveaux résultats.
Il est dû à Yitang Zhang. L’énoncé le plus simple de ce qu’il a prouvé est qu’il existe un nombre infini d’intervalles $[n, n+70 000 000)$ contenant au moins deux nombres premiers. Cette affirmation est plus faible que la conjecture des nombres premiers jumeaux, mais elle en est conceptuellement très proche. Dans des travaux ultérieurs (par de nombreux mathématiciens), la taille de l’écart a été sévèrement réduite, mais il n’y a vraisemblablement aucun moyen de le réduire à $2$ avec les méthodes actuelles.
Comme l’explique Granville, le premier et sans doute le principal résultat de Zhang est qu’il existe $k$ avec la propriété que si $a_{1}$, $\ldots$ , $a_{k}$ est un ensemble admissible de $k$ éléments, alors il existe un nombre infini de $n$ tels que $\{ n +a_{i} \}$ contienne au moins deux nombres premiers. (Dans l’article Quanta de Klarreich, le tableau est appelé un « peigne ». Gardez à l’esprit que selon la conjecture de Dickson, nous nous attendrions à pouvoir dire que tous les $k$ sont des nombres premiers). En fait, Zhang a prouvé que cette affirmation était vraie pour un nombre particulier de $k =3 500 000$ couvrant un intervalle de $70 000 000$. La conséquence désormais célèbre est pour un certain $m \lt 70 000 000$ qu’il existe un nombre infini de paires de nombres premiers $p$, $p+m$.
Lecture complémentaire
- Lord Cherwell et E. M. Wright, « The frequency of prime patterns », The Quarterly Journal of Mathematics 11 (1960).
Ceux qui connaissent un peu la vie de Lord Cherwell, autrement connu sous le nom de Frederick Lindemann, seront très surpris d’apprendre sa contribution à la théorie des nombres. La biographie Wikipedia ne suggère pas de manière adéquate toutes les raisons de sa mauvaise réputation en tant que principal conseiller scientifique de Churchill pendant la Seconde Guerre mondiale.
- L. E. Dickson, « Une nouvelle extension du théorème de Dirichlet sur les nombres premiers », Messenger of Mathematics 33.
Voir aussi l’entrée Wikipedia sur la conjecture de Dickson.
- Andrew Granville, « Les nombres premiers dans les intervalles de longueur bornée ». Disponible sur sa page d’accueil.
- G. H. Hardy, Ramanujan, Cambridge University Press.
La section 2.5 contient une dérivation idéale d’une formule possible pour $\pi(x)$.
- G. H. Hardy et J. E.. Littlewood, « Some problems of ‘Partitio numerorum’ III : on the expression of a number as a sum of primes », Acta Mathematica 44 (1923).
- G. H. Hardy et E. M. Wright, The theory of numbers, Oxford Press.
- Erica Klarreich, « Together and alone, closing the prime gap », Quanta 19 novembre 2013.
- B. Riemann, « Sur le nombre de nombres premiers inférieurs à une quantité donnée ». Une traduction anglaise de ce classique par David Wilkins est disponible à partir d’un lien dans Wikipedia.
Entre autres choses, cela esquisse une dérivation de la formule approximative de $\pi(x)$.
- J. W. Wrench, « Evaluation de la constante d’Artin et de la constante twin-prime », Mathematics of Computation 76 (1961).
Un calcul précoce de $C_{2}$.
- Listes de nombres premiers jusqu’à 1 000 000 000 000$
- Une liste des 20 000 premiers nombres premiers jumeaux.
 Bill Casselman
Bill Casselman
Université de la Colombie-Britannique, Vancouver, Canada
Email Bill Casselman
.