Modélisation mathématique

by admin Leave Comment

Objectifs d’apprentissage

  • Introduction aux fonctions par morceaux
    • Définition d’une fonction par morceaux. fonction
    • Evaluer une fonction par morceaux
    • Ecrire une fonction par morceaux compte tenu d’une application
  • Graphier des fonctions par morceaux
    • Sous réserve d’une fonction définie par morceaux.définie par morceaux, esquissez un graphique
    • Écrivez le domaine et l’étendue d’une fonction par morceaux étant donné un graphique

Certaines fonctions sont en morceaux. Dans cette section, nous allons apprendre à définir et à tracer des graphiques de fonctions qui sont essentiellement des collections de pièces discrètes. Parmi les exemples de fonctions définies de cette manière, citons la conception du profil d’une voiture, le calcul de votre forfait de téléphonie mobile et le calcul des taux d’imposition sur le revenu. Par exemple, votre taux d’imposition dépend de votre revenu et est le même pour une gamme de revenus, comme le montre le tableau ci-dessous :

Taux marginal d’imposition Revenu imposable d’une personne seule Revenu imposable d’un couple marié ou d’un veuf qualifié(er). revenu imposable Marié déclarant séparément revenu imposable Revenu imposable du chef de famille
10% $0 – $9,275 $0 – $18,550 $0 – $9,275 $0 – $13,250
15% $9,276 – $37,650 $18,551 – $75,300 $9,276 – $37,650 $13,251 – $50,400
25% $37,651 – $91,150 $75,301 – $151,900 $37,651 – $75,950 $50,401 – $130,150
28% $91,151 – $190,150 $151,901 – $231,450 $75,951 – $115,725 $130,151 – $210,800
33% $190,151 – $413,350 $231,451 – $413,350 $115,726 – $206,675 $210,801 – $413,350
35% $413,351 – $415,050 $413,351 – $466,950 $206,676 – $233,475 $413,351 – $441,000
39.6% 415,051+ 466,951+ 233,476+ 441,001+

Une fonction par morceaux est une fonction dans laquelle plus d’une formule est utilisée pour définir la sortie sur différents morceaux du domaine.

Nous utilisons les fonctions par morceaux pour décrire des situations dans lesquelles une règle ou une relation change lorsque la valeur d’entrée franchit certaines « frontières ». Par exemple, nous rencontrons souvent des situations dans le monde des affaires pour lesquelles le coût par pièce d’un certain article est escompté dès que le nombre commandé dépasse une certaine valeur. Les tranches d’imposition sont un autre exemple concret de fonctions par morceaux. Prenons l’exemple d’un système fiscal simple dans lequel les revenus jusqu’à 10 000 dollars sont imposés à 10 %, et tout revenu supplémentaire à 20 %. L’impôt sur un revenu total, S, serait de 0,1S si S\le 10 000 $ et 1000 + 0,2 (S – 10 000 $), si S> 10 000 $.

Fonction par morceaux

Une fonction par morceaux est une fonction dans laquelle plus d’une formule est utilisée pour définir la sortie. Chaque formule a son propre domaine, et le domaine de la fonction est l’union de tous ces petits domaines. On note cette idée comme suit :

f\left(x\right)=\begin{cases}\text{formule 1 si x est dans le domaine 1}\\text{formule 2 si x est dans le domaine 2}\ \text{formule 3 si x est dans le domaine 3}\end{cases}

En notation par morceaux, la fonction de valeur absolue est

|x|=\begin{cases}x\text{si }x\ge 0\\\ -x\text{si }x<0\end{cases}

Evaluer une fonction définie par morceaux

Dans le premier exemple, nous allons montrer comment évaluer une fonction définie par morceaux. Notez comment il est important de prêter attention au domaine pour déterminer l’expression à utiliser pour évaluer l’entrée.

Exemple

Donné la fonction

f(x)=\begin{cases}7x+3\text{ si }x<0\\7x+6\text{ si }x\ge{0}\end{cases},

évaluer :

  1. f (-1)
  2. f (0)
  3. f (2)
Afficher la réponse

1.f(x) est définie comme 7x+3 pour x=-1\text{ parce que }-1<0.

Evaluez : f(-1)=7(-1)+3=-7+3=-4

2. f(x) est définie comme 7x+6 pour x=0\text{ parce que }0\ge{0}.

Evaluer : f(0)=7(0)+6=0+6=6

3. f(x) est définie comme 7x+6 pour x=2\text{ parce que }2\ge{0}.

Evaluer : f(2)=7(2)+6=14+6=20

Dans la vidéo suivante, nous montrons comment évaluer plusieurs valeurs étant donné une fonction définie par morceaux.

Dans l’exemple suivant, nous montrons comment évaluer une fonction qui modélise le coût du transfert de données pour une compagnie de téléphone.

Exemple

Une compagnie de téléphone cellulaire utilise la fonction ci-dessous pour déterminer le coût, C, en dollars pour g gigaoctets de transfert de données.

C\left(g\right)=\begin{cases}{25}\text{ if }{ 0 }<{ g }<{ 2 }\\\\{10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

Trouve le coût de l’utilisation de 1.5 gigaoctets de données et le coût d’utilisation de 4 gigaoctets de données.

Afficher la réponse

Pour trouver le coût d’utilisation de 1,5 gigaoctets de données, C(1,5), nous regardons d’abord dans quelle partie du domaine notre entrée tombe. Comme 1,5 est inférieur à 2, nous utilisons la première formule.

C(1,5) = 25$

Pour trouver le coût d’utilisation de 4 gigaoctets de données, C(4), nous voyons que notre entrée de 4 est supérieure à 2, donc nous utilisons la deuxième formule.

C(4)=10(4)+5=45

Analyse de la solution

La fonction est représentée dans le graphique ci-dessous. Nous pouvons voir où la fonction passe d’une constante à une droite avec une pente positive à g=2. Nous traçons les graphiques des différentes formules sur un ensemble commun d’axes, en nous assurant que chaque formule est appliquée sur son propre domaine.

C(g) = C\left(g\right)=\begin{cases}{25}\text{ if }{ 0 }<{ g }<{ 2 }\\\\text{ if }{ g}\ge{ 2 }\end{cases}

Écrire une fonction définie par morceaux

Dans le dernier exemple, nous allons montrer comment écrire une fonction définie par morceaux qui modélise le prix d’une visite guidée de musée.

Exemple

Un musée demande 5 $ par personne pour une visite guidée avec un groupe de 1 à 9 personnes ou un tarif fixe de 50 $ pour un groupe de 10 personnes ou plus. Ecrivez une fonction reliant le nombre de personnes, n, au coût, C.

Afficher la réponse

Deux formules différentes seront nécessaires. Pour les valeurs de n inférieures à 10, C=5n. Pour les valeurs de n supérieures ou égales à 10, C=50.

C(n)=\begin{cases}{5n}\text{ if }{0}<{n}<{10}\ 50\text{ if }{n}\ge 10\end{cases}

Analyse de la solution

La fonction est représentée sur la figure 21. Le graphique est une ligne diagonale de n=0 à n=10 et une constante après cela. Dans cet exemple, les deux formules s’accordent au point de rencontre où n=10, mais toutes les fonctions par morceaux n’ont pas cette propriété.

Dans la vidéo suivante, nous montrons un exemple d’écriture d’une fonction définie par morceaux étant donné un scénario.

Donné une fonction par morceaux, écrivez la formule et identifiez le domaine pour chaque intervalle.

  1. Identifier les intervalles pour lesquels différentes règles s’appliquent.
  2. Déterminer les formules qui décrivent comment calculer une sortie à partir d’une entrée dans chaque intervalle.
  3. Utiliser les accolades et les déclarations if pour écrire la fonction.

Graphier des fonctions par morceaux

Dans cette section, nous allons tracer des fonctions par morceaux. La fonction tracée ci-dessous représente le coût de transfert des données pour une compagnie de téléphonie cellulaire donnée. Nous pouvons voir où la fonction passe d’une constante à une ligne avec une pente positive à g=2. Lorsque nous traçons des fonctions par morceaux, il est important de s’assurer que chaque formule est appliquée à son propre domaine.C\left(g\right)=\begin{cases}{25} \text{ if }{ 0 }<{ g }<{ 2 }\\\\_10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

Dans ce cas, la sortie est 25 pour toute entrée entre 0 et 2. Pour les valeurs égales ou supérieures à 2, la sortie est définie comme 10g+5.

Donné une fonction par morceaux, esquissez un graphique.

  1. Indiquez sur l’axe des x les limites définies par les intervalles sur chaque morceau du domaine.
  2. Pour chaque morceau du domaine, faites un graphique sur cet intervalle en utilisant l’équation correspondante se rapportant à ce morceau. Ne représentez pas deux fonctions sur un seul intervalle car cela violerait les critères d’une fonction.

Exemple

Esquissez un graphique de la fonction.

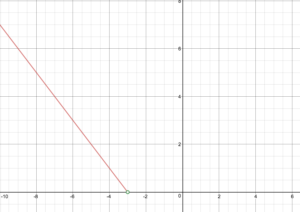
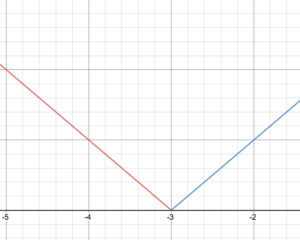
Donné la définition par morceaux f(x)=\begin{cases}-x – 3\text{ if }x < -3\\ x + 3\text{ if }. x \ge -3\end{cases}
Dessinez le graphique de f.
Indiquez le domaine et l’étendue de la fonction.

Afficher la réponse

D’abord, tracez le graphique de la ligne f(x) = -x-3, en effaçant la partie où x est supérieur à -3. Placez un cercle ouvert à (-3,0).

Placez maintenant la ligne f(x) = x+3 sur le graphique, en commençant au point (-3,0). Notez que pour cette partie du graphique, le point (-3,0) est inclus, vous pouvez donc supprimer le cercle ouvert.

Les deux graphiques se rejoignent au point (-3,0)

Le domaine de cette fonction est l’ensemble des nombres réels car (-3,0)n’est pas inclus comme point d’arrivée de f(x) = -x-3, mais il est inclus comme point d’arrivée de f(x) = x+3.

L’étendue de cette fonction commence à f(x)=0 et inclut 0, et va jusqu’à l’infini, donc nous écririons ceci comme x\ge0

Dans l’exemple suivant, nous allons tracer une fonction définie par morceaux qui modélise le coût de l’expédition pour un détaillant de bandes dessinées en ligne.

Exemple

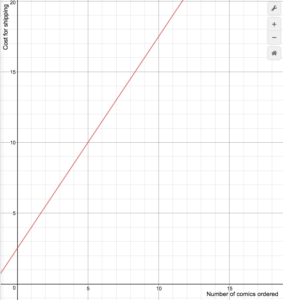
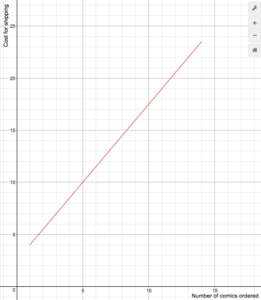
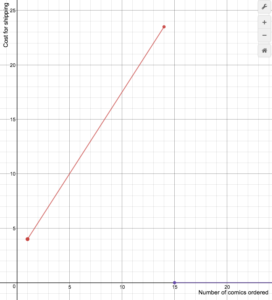
Un détaillant de bandes dessinées en ligne facture les frais d’expédition selon la formule suivante

S(n)=\begin{cases}1.5n+2.5\text{ if }1\le{n}\le14\\0\text{ if }n\ge15\end{cases}

Dessinez un graphique de la fonction de coût.

Show Answer

D’abord, tracez la ligne S(n)=1,5n+2,5. On peut utiliser des transformations : c’est un étirement vertical de l’identité d’un facteur 1,5, et un décalage vertical de 2,5.

S(n)=1,5n+2.5

Maintenant, on peut éliminer les portions du graphique qui ne sont pas dans le domaine en se basant sur 1\le{n}\le14

S(n) = 1,5n+2,5 pour 1<=n<=14

Enfin, on ajoute la fonction constante S(n)=0 pour les entrées supérieures ou égales à 15. Placez des points fermés sur les extrémités du graphique pour indiquer l’inclusion des points extrêmes.

Dans la vidéo suivante, nous montrons comment tracer le graphique d’une fonction définie par morceaux qui est linéaire sur les deux domaines.

Sommaire

  • Une fonction définie par morceaux est une fonction dans laquelle plus d’une formule est utilisée pour définir la sortie sur différents morceaux du domaine.
  • Evaluer une fonction définie par morceaux signifie que vous devez prêter une attention particulière à l’expression correcte utilisée pour l’entrée donnée

Pour graphier des fonctions définies par morceaux, identifiez d’abord où le domaine est divisé. Graphiquez les fonctions sur le domaine en utilisant des outils tels que les points de traçage, ou les transformations. Faites attention à utiliser des cercles ouverts ou fermés sur les points d’extrémité de chaque domaine en fonction de l’inclusion ou non du point d’extrémité.

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée.