Commençons par examiner la division de valeurs avec des exposants.
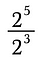
Rappelons que les exposants représentent une multiplication répétée. Nous pouvons donc réécrire l’expression ci-dessus comme:
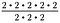
Puisque 2/2 = 1, annulez trois ensembles de 2/2. Il reste donc 2 – 2, ou 2 au carré.
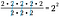
Bien sûr, nous pouvons prendre un raccourci et soustraire le nombre de 2 du bas du nombre de 2 du haut. Comme ces quantités sont représentées par leurs exposants respectifs, tout ce que nous avons à faire est d’écrire la base commune avec la différence des valeurs des exposants comme puissance.
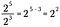
Si nous généralisons cette règle, nous avons ce qui suit où n représente un nombre réel non nul et x et y sont également des nombres réels.
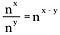
Exploration de la puissance zéro
À partir de là, il est facile de déduire l’explication de la raison pour laquelle tout nombre non nul élevé à la puissance zéro est égal à 1. Encore une fois, prenons un exemple concret.
Nous savons que tout nombre non nul divisé par lui-même est égal à 1. Je peux donc écrire ce qui suit :
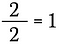
Cela revient à écrire :
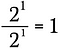
Je vais maintenant utiliser la règle des exposants pour réécrire le côté gauche de cette équation.
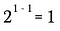
Bien sûr, ceci est équivalent à :
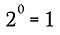
On peut utiliser le même procédé que dans cet exemple, ainsi que la règle généralisée ci-dessus, pour montrer que tout nombre réel non nul élevé à la puissance zéro doit donner 1.
Qu’en est-il de zéro puissance zéro ?
C’est là que les choses se compliquent. La méthode ci-dessus se brise parce que, bien sûr, la division par zéro est un non-non. Examinons pourquoi.
Nous commencerons par examiner une ERREUR commune de division par zéro.
Que diriez-vous de 2÷0 ? Voyons pourquoi nous ne pouvons pas le faire.
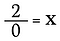
La division n’est en fait qu’une forme de multiplication, alors que se passe-t-il si je réécris l’équation ci-dessus comme :
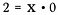
Quelle valeur pourrait éventuellement satisfaire cette équation pour x ?
Il n’y a aucune valeur ! Tout nombre multiplié par zéro donne zéro, il ne peut jamais être égal à 2. Par conséquent, nous disons que la division par zéro est indéfinie. Il n’y a pas de solution possible.
Maintenant, regardons 0÷0.
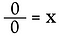
De nouveau, réécrivons-le comme un problème de multiplication.
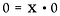
Ici nous rencontrons une situation très différente. La solution pour x pourrait être N’IMPORTE QUEL nombre réel ! Il n’y a aucun moyen de déterminer ce qu’est x. Par conséquent, 0/0 est considéré comme indéterminé*, et non indéfini.
Si nous essayons d’utiliser la méthode ci-dessus avec zéro comme base pour déterminer ce que serait zéro puissance zéro, nous nous arrêtons immédiatement et ne pouvons pas continuer parce que nous savons que 0÷0 ≠ 1, mais est indéterminé.
Alors, qu’est-ce que zéro puissance zéro égale ?
Cela est très débattu. Certains croient qu’il devrait être défini comme 1 tandis que d’autres pensent que c’est 0, et certains croient qu’il est indéfini. Il y a de bons arguments mathématiques pour chacun, et peut-être est-il plus correctement considéré comme indéterminé.
Malgré cela, la communauté mathématique est en faveur de la définition de zéro puissance zéro comme 1, au moins pour la plupart des objectifs.
Peut-être qu’une définition utile des exposants pour le mathématicien amateur est la suivante:
.