La formule standard pour trouver le déterminant d’une matrice 3×3 est une décomposition de plus petits problèmes de déterminant 2×2 qui sont très faciles à traiter. Si vous avez besoin d’un rafraîchissement, consultez mon autre leçon sur la façon de trouver le déterminant d’une 2×2. Supposons que l’on nous donne une matrice carrée A où,
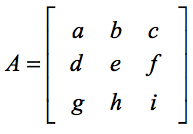
Le déterminant de la matrice A est calculé comme
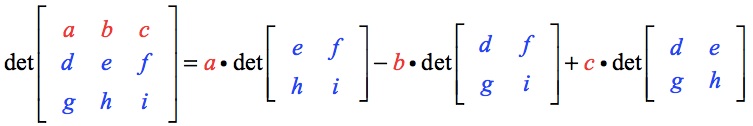
Voici les points clés:
- Notez que les éléments de la ligne supérieure à savoir a, b et c servent de multiplicateurs scalaires à une matrice 2×2 correspondante.
- Le scalaire a est multiplié à la matrice 2×2 des éléments restants créés lorsque les segments de ligne verticaux et horizontaux sont dessinés en passant par a.
- Le même processus est appliqué pour construire les matrices 2×2 pour les multiplicateurs scalaires b et c.
Déterminant d’une matrice 3 x 3 (animé)

Exemples de comment trouver le déterminant d’une matrice 3×3
Exemple 1 : Trouvez le déterminant de la matrice 3×3 ci-dessous.
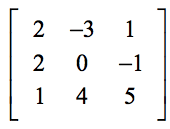
Le montage ci-dessous vous aidera à trouver la correspondance entre les éléments génériques de la formule et les éléments du problème réel.
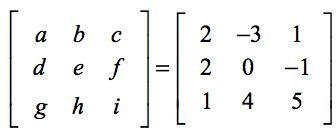
En appliquant la formule,


Exemple 2 : évaluez le déterminant de la matrice 3×3 ci-dessous.
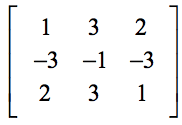
Faites très attention lorsque vous substituez les valeurs aux bons endroits dans la formule. Les erreurs courantes se produisent lorsque les étudiants deviennent négligents pendant l’étape initiale de substitution des valeurs.
En outre, prenez votre temps pour vous assurer que votre arithmétique est également correcte. Sinon, une seule erreur quelque part dans le calcul donnera une mauvaise réponse au final.
Depuis,
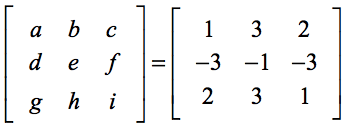
notre calcul du déterminant devient…

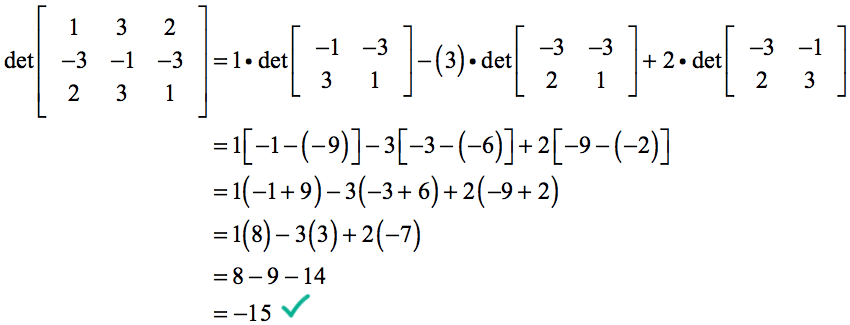
Exemple 3 : Résolvez le déterminant de la matrice 3×3 ci-dessous.
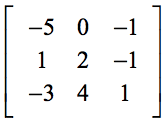
La présence du zéro (0) dans la première ligne devrait rendre notre calcul beaucoup plus facile. Rappelez-vous, ces éléments dans la première ligne, agissent comme des multiplicateurs scalaires. Par conséquent, le zéro multiplié à quoi que ce soit entraînera la disparition de l’expression entière.