Préalable – Mesures de distance en Data Mining
En Data Mining, la mesure de similarité fait référence à la distance avec les dimensions représentant les caractéristiques de l’objet de données, dans un ensemble de données. Si cette distance est moindre, il y aura un haut degré de similarité, mais lorsque la distance est grande, il y aura un faible degré de similarité.
Certaines des mesures de similarité populaires sont –
- Distance euclidienne.
- Distance Manhattan.
- Similarité Jaccard.
- Distance Minkowski.
- Similarité cosinus.
La similarité cosinus est une métrique, utile pour déterminer, à quel point les objets de données sont similaires indépendamment de leur taille. Nous pouvons mesurer la similarité entre deux phrases en Python en utilisant la similarité cosinus. Dans la similarité cosinus, les objets de données d’un ensemble de données sont traités comme un vecteur. La formule pour trouver la similarité cosinus entre deux vecteurs est –
Cos(x, y) = x . y / ||x|| * ||y||
où,
- x . y = produit (point) des vecteurs ‘x’ et ‘y’.
- ||x|| et ||y|| = longueur des deux vecteurs ‘x’ et ‘y’.
- ||x|| * ||y|| = produit en croix des deux vecteurs ‘x’ et ‘y’.
Exemple :
Considérez un exemple pour trouver la similarité entre deux vecteurs – ‘x’ et ‘y’, en utilisant la similarité en cosinus.
Le vecteur ‘x’ a pour valeurs, x = { 3, 2, 0, 5 }
Le vecteur ‘y’ a pour valeurs, y = { 1, 0, 0, 0 }
La formule pour calculer la similarité en cosinus est : Cos(x, y) = x . y / ||x|| * ||y||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1∴ Cos(x, y) = 3 / (6.16 * 1) = 0.49
La dissimilarité entre les deux vecteurs ‘x’ et ‘y’ est donnée par –
∴ Dis(x, y) = 1 - Cos(x, y) = 1 - 0.49 = 0.51
- La similitude en cosinus entre deux vecteurs se mesure en ‘θ’.
- Si θ = 0°, les vecteurs ‘x’ et ‘y’ se chevauchent, ce qui prouve qu’ils sont semblables.
- Si θ = 90°, les vecteurs ‘x’ et ‘y’ sont dissemblables.
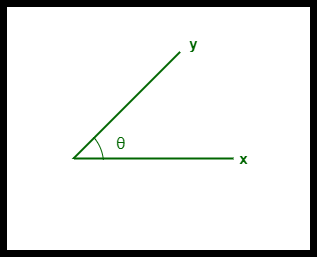
Similitude en cosinus entre deux vecteurs
Avantages :
- La similitude en cosinus est bénéfique car même si les deux objets de données similaires sont éloignés par la distance euclidienne en raison de leur taille, ils pourraient toujours avoir un angle plus petit entre eux. Plus l’angle est petit, plus la similarité est élevée.
- Lorsqu’elle est tracée sur un espace multidimensionnel, la similarité cosinus capte l’orientation (l’angle) des objets de données et non la magnitude.