Circuit demi-additionneur et additionneur complet
Les circuits demi-additionneur et additionneur complet sont expliqués avec leurs tables de vérité dans cet article. La conception d’un additionneur complet utilisant un circuit demi-additionneur est également présentée. Le circuit de l’additionneur complet à un bit et l’addition à plusieurs bits utilisant l’additionneur complet sont également montrés.
Avant d’entrer dans ce sujet, il est très important de connaître la logique booléenne et les portes logiques.
Voir : la logique booléenne
Voir : les portes logiques
Voir : les FLIP FLOPS
Qu’est-ce qu’un additionneur ?
Un additionneur est une sorte de calculatrice qui est utilisée pour ajouter deux nombres binaires. Quand je dis, calculatrice, je ne veux pas dire une avec des boutons, celle-ci est un circuit qui peut être intégré avec beaucoup d’autres circuits pour une large gamme d’applications. Il existe deux types d’additionneurs;
- Demi-additionneur
- Additionneur complet
Demi-additionneur
A l’aide du demi-additionneur, nous pouvons concevoir des circuits capables d’effectuer une addition simple à l’aide de portes logiques.
Regardons d’abord l’addition de bits simples.
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
Ce sont les combinaisons de bits simples les moins possibles. Mais le résultat pour 1+1 est 10. Bien que ce problème puisse être résolu à l’aide d’une porte EXOR, si vous vous souciez de la sortie, le résultat de la somme doit être réécrit comme une sortie de 2 bits.
Donc les équations ci-dessus peuvent être écrites comme
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
Ici, la sortie ‘1’de ’10’ devient le report. Le résultat est montré dans une table de vérité ci-dessous. SUM » est la sortie normale et « CARRY » est le report.
INPUTS OUTPUTS
A B SUM CARRY
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
D’après l’équation, il est clair que cet additionneur 1 bit peut être facilement implémenté à l’aide d’une porte EXOR pour la sortie ‘SUM’ et d’une porte AND pour la retenue. Jetez un coup d’œil à la mise en œuvre ci-dessous.
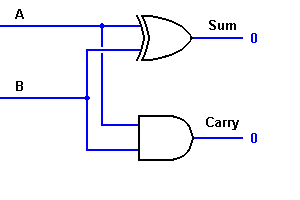
Pour une addition complexe, il peut y avoir des cas où vous devez ajouter deux octets de 8 bits ensemble. Cela ne peut être fait qu’avec l’aide de la logique d’addition complète.
Addition complète
Ce type d’additionneur est un peu plus difficile à mettre en œuvre qu’un demi-additionneur. La principale différence entre un demi-adder et un full-adder est que le full-adder a trois entrées et deux sorties. Les deux premières entrées sont A et B et la troisième entrée est une entrée de report désignée par CIN. Lorsqu’une logique d’additionneur complet sera conçue, nous pourrons en enchaîner huit pour créer un additionneur de la largeur d’un octet et cascader le bit de retenue d’un additionneur au suivant.
La retenue de sortie est désignée par COUT et la sortie normale est désignée par S. Jetez un coup d’œil à la table de vérité.
ENTRÉES SORTIES
A B CIN COUT S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1
D’après la table de vérité ci-dessus.ci-dessus, la logique de l’additionneur complet peut être implémentée. Nous pouvons voir que la sortie S est un EXOR entre l’entrée A et la sortie SUM du demi-additionneur avec les entrées B et CIN. Nous devons également noter que le COUT ne sera vrai que si l’une des deux entrées sur les trois est HIGH.
Ainsi, nous pouvons implémenter un circuit additionneur complet à l’aide de deux circuits demi-additionneurs. Le premier demi-additionneur sera utilisé pour ajouter A et B pour produire une somme partielle. La seconde logique de demi-addition peut être utilisée pour ajouter CIN à la somme produite par le premier demi-additionneur pour obtenir la sortie S finale. Si l’une des logiques du demi-additionneur produit une retenue, il y aura une retenue en sortie. Ainsi, COUT sera une fonction OU des sorties Carry du demi-additionneur. Jetez un coup d’œil à la mise en œuvre du circuit d’additionneur complet présenté ci-dessous.
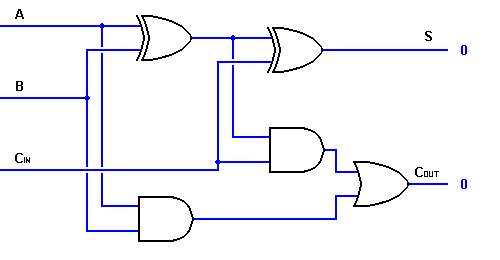
Bien que la mise en œuvre de plus grands diagrammes logiques soit possible avec la logique d’additionneur complet ci-dessus, un symbole plus simple est le plus souvent utilisé pour représenter l’opération. Donné ci-dessous est une représentation schématique plus simple d’un additionneur complet à un bit.
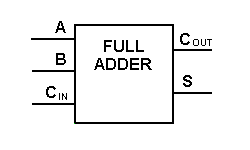
Avec ce type de symbole, nous pouvons ajouter deux bits ensemble en prenant une retenue de l’ordre de grandeur inférieur suivant, et en envoyant une retenue à l’ordre de grandeur supérieur suivant. Dans un ordinateur, pour une opération multibit, chaque bit doit être représenté par un additionneur complet et doit être ajouté simultanément. Ainsi, pour additionner deux nombres de 8 bits, il faut 8 additionneurs complets qui peuvent être formés en cascadant deux des blocs de 4 bits. L’addition de deux nombres de 4 bits est illustrée ci-dessous.
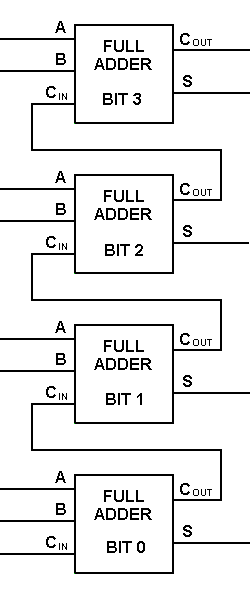
.