Une élève de quatrième année, Alice, demande : « Combien de diagonales y a-t-il dans un décagone ? »
Grande question, Alice. Mais au lieu de te donner une réponse à cette question, je vais te montrer comment tu peux le découvrir par toi-même. Et pas seulement ça, je vais te montrer comment tu peux trouver la réponse pour n’importe quel polygone, même s’il a 20, ou 50, ou 2000 côtés!
Prête ? Commençons par un exemple simple. Nous allons prendre un polygone qui a 8 côtés (que l’on appelle un octogone), comme ceci :
Maintenant, ce polygone, parce qu’il a huit côtés, a aussi huit sommets. Il semble un peu écrasant d’essayer de comprendre toutes les diagonales, alors concentrons-nous sur un seul sommet. Combien de diagonales pouvez-vous dessiner dans un octogone, qui commencent toutes à un sommet ?
La réponse à cette question est cinq. Regardez le diagramme ci-dessous :

Dans ce diagramme, j’ai choisi la diagonale à gauche juste en dessous du sommet supérieur, et j’ai tracé des diagonales vers tous les sommets vers lesquels je peux tracer une diagonale. Sur quelles diagonales ne puis-je pas tracer de diagonales ? Eh bien, je ne peux pas dessiner une diagonale d’un sommet vers lui-même, et je ne peux pas dessiner de diagonales vers les deux sommets à côté de celui-ci (parce que ce ne seraient pas des diagonales ; ce seraient des côtés !).
Donc il y a trois sommets vers lesquels je ne peux pas dessiner de diagonales à partir de ce sommet. Huit sommets au total, moins les trois vers lesquels je ne peux pas dessiner, il en reste cinq. C’est important à retenir : soustrayez 3 du nombre de sommets, et vous avez le nombre de diagonales que vous pouvez dessiner à partir de n’importe quel sommet.
Mais ce n’est qu’un seul sommet ! Tu pourrais dessiner des diagonales à partir de n’importe quel sommet, non ? Bien sûr ! Et il y a huit sommets dans notre octogone, donc on prend le nombre de diagonales par sommet, et on le multiplie par le nombre de sommets : 5 x 8 = 40.
Vous pourriez être tenté de penser que c’est notre réponse, mais ce n’est pas le cas. Pourquoi pas ? Parce que nous avons compté chaque diagonale deux fois ! Chaque diagonale a deux sommets, donc nous l’avons comptée depuis une extrémité, et nous l’avons également comptée depuis l’autre extrémité. Pour obtenir le nombre réel de diagonales, nous devons donc diviser notre réponse par 2. 40 / 2 = 20. Il y a vingt diagonales dans un octogone.
Tentons ce raisonnement sur un polygone qui a 2000 côtés. Maintenant, je ne vais pas vous dessiner un polygone de 2000 côtés ; nous devrons juste travailler sur le raisonnement sans image.
- Posez un sommet. Combien de diagonales pouvez-vous tracer à partir de ce sommet ? Réponse : 2000 – 3 = 1997.
- Combien de sommets au total ? Réponse : 2000
- Combien de diagonales comptées à partir de tous les sommets ? Réponse : 1997 x 2000 = 3 994 000
- Oops ! Nous avons compté chaque diagonale deux fois ! Comment se débarrasser des doublons ? Réponse : 3994000 / 2 = 1,997,000
Donc un 2000-gon a 1,997,000 diagonales!
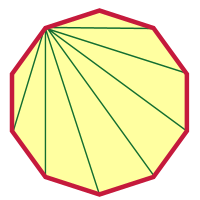
Après avoir fait quelque chose d’aussi fou qu’un 2000-gon, un décagone ne devrait pas sembler si difficile, non ? Je vais te faire commencer, et tu pourras le terminer à partir de là. J’ai choisi un sommet et j’ai dessiné des diagonales à partir de ce sommet.
Combien y en a-t-il ? Avez-vous été capable de déterminer combien il y en avait sans regarder l’image ?
Pouvez-vous le déterminer à partir d’ici ? Je l’espère ! Bonne chance, Alice.
A propos, il y a une formule que vous pouvez utiliser ; elle ressemble à ceci : D = n(n – 3)/2. Mais honnêtement, je n’attends pas de mes étudiants qu’ils la mémorisent. J’attends d’eux qu’ils se souviennent de la façon dont nous raisonnons ici. Si vous comprenez la logique, c’est encore mieux que d’avoir une formule !