Thèmes de la chimie générale
Énergie : Concepts fondamentaux
Formes d’énergie : Cinétique et potentielle.Travail et énergie.Chaleur et température.Énergie potentielle électrostatique.
Énergie : cinétique et potentielle
Le concept d’énergie est fondamental pour les sciences physiques. Nous visons ici à énoncer quelques premiers principes concernant l’énergie, et à présenter certaines des formes que prend l’énergie et qui sont particulièrement importantes pour la chimie. Tout d’abord, il est souvent très utile de définir un système pour désigner une partie particulière de l’univers sur laquelle nos observations sont effectuées. Le système est constitué d’un objet ou d’une collection d’objets, et se distingue du reste de l’univers – que nous appelons l’environnement – par une frontière réelle ou imaginaire.
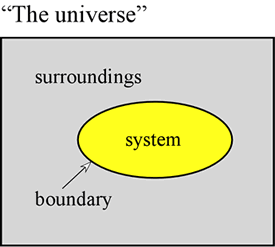
Un échantillon de gaz contenu dans un volume fixe, tel qu’un cylindre métallique, est un exemple de système – un système qui nous sera utile lorsque nous aborderons l’étude des propriétés générales des gaz. D’autres exemples sont un échantillon de gaz dans un ballon ou un mélange de combustion dans un cylindre avec un piston. Dans ces deux cas, le système est entouré d’une frontière physique, mais mobile, de sorte que le volume du système n’est pas fixe. Un autre exemple que nous considérerons souvent est celui d’un mélange de substances en solution subissant une réaction chimique dans un tube à essai ou un bécher. La terminologie introduite ici revêt une importance particulière dans l’étude de la façon dont l’énergie se manifeste dans les systèmes chimiques, qui relève en grande partie de la thermodynamique.
En chimie générale, les systèmes que nous considérons comme pertinents sont généralement au repos et les effets gravitationnels sont ignorés. Souvent, nous nous intéressons surtout aux systèmes au sein desquels des réactions chimiques ont lieu, la composition chimique du système évoluant avec le temps. Adoptons cependant pour le moment une perspective plus large en utilisant des systèmes mécaniques tels qu’un pendule oscillant, ou des boules de billard qui roulent et entrent en collision, pour nous aider à comprendre les principes généraux relatifs à l’énergie.
On peut dire qu’un système possède de l’énergie de deux manières différentes, que nous appelons énergie cinétique et énergie potentielle. L’énergie cinétique est l’énergie de la matière en mouvement. La physique fournit une définition mathématique exacte de l’énergie cinétique (KE), représentée par l’équation (ci-dessous à gauche).
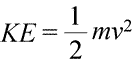
Ici, l’énergie cinétique d’un objet est représentée comme un produit de la masse de l’objet (m) et du carré de sa vitesse (v), multiplié également par la constante ½. Si le système est composé de plus d’un objet, l’énergie cinétique totale est exprimable comme une somme des énergies cinétiques des objets individuels.
Nous pouvons dériver des unités pour l’énergie étant donné cette définition. L’unité SI pour l’énergie est le joule (J), qui est défini comme:
1 J = 1 kg-m-s-2
L’énergie potentielle est l’énergie d’un système qui peut typiquement être convertie en énergie cinétique sous une certaine forme, et capable de produire, dans une certaine mesure, une quantité appelée travail (discuté plus loin). Un exemple clair d’énergie potentielle est une brique sur le rebord d’un bâtiment. La brique possède une certaine quantité d’énergie potentielle en raison de sa hauteur, c’est-à-dire de sa position par rapport à un champ gravitationnel. Si nous donnons un coup de coude à la brique pour qu’elle tombe du rebord, elle se déplace spontanément dans la direction de l’énergie potentielle gravitationnelle la plus faible et, ce faisant, elle acquiert de l’énergie cinétique. Un autre exemple est l’énergie potentielle électrique d’une batterie (qui s’exprime en termes de tension). Lorsqu’un circuit est réalisé avec un fil et une ampoule, reliant les deux bornes d’une batterie, la différence de potentiel électrique entre eux fait bouger les électrons dans le fil (énergie cinétique), ce qui entraîne la production à la fois de chaleur et de lumière.
Un principe général important concernant l’énergie est qu’elle ne peut être ni créée ni détruite. C’est ce que l’on appelle la loi de la conservation de l’énergie. Quantitativement, cela signifie que dans un système tel que la brique qui tombe ou le pendule d’une horloge, la somme des énergies cinétique et potentielle est constante. Il s’agit en quelque sorte d’une abstraction, car dans un pendule réel, une partie de l’énergie est continuellement perdue en raison de la friction, et une petite quantité d’énergie doit être ajoutée au pendule pour qu’il continue à se balancer (et que l’horloge fonctionne). Mais si l’on tient compte de cette énergie « perdue » (qui apparaît en fait comme une augmentation de l’énergie thermique des molécules d’air environnantes) par des mesures expérimentales minutieuses, on constate que l’énergie est toujours conservée. Une autre mise en garde est résumée dans la célèbre équation d’Einstein E = mc2, qui exprime une équivalence fondamentale entre la masse et l’énergie. Une forme plus générale de la loi de conservation de l’énergie, que l’on peut appeler la loi de conservation de la masse et de l’énergie, rend compte de cette équivalence. Pour en revenir à la chimie générale, ces interconversions matière-énergie ne sont pas typiquement de son ressort, alors que l’étude des réactions nucléaires et de la radioactivité est englobée par la physique nucléaire.
Si l’on considère une réaction chimique dans laquelle les changements chimiques s’accompagnent d’une production de chaleur, une question se pose : Qu’en est-il de la conservation de l’énergie dans ce cas ? La réponse est qu’il existe une forme d’énergie potentielle, que nous pouvons appeler énergie potentielle chimique (ou simplement potentiel chimique), que l’on peut considérer comme résidant dans la composition moléculaire des réactifs. Cette énergie potentielle est ensuite convertie en énergie sous forme de chaleur, mais il s’avère que la quantité nette d’énergie présente reste constante, une fois que nous sommes capables de définir et de mesurer la production de chaleur. Un exemple quotidien de ce que nous pouvons maintenant comprendre comme l’énergie potentielle chimique est donné par un moteur à essence, dans lequel le mélange d’essence et d’oxygène possède une forme d’énergie latente. Cette énergie latente dans le mélange essence/oxygène est dépensée pour produire l’énergie cinétique d’une voiture.
Travail et énergie
Le travail est un autre concept qui admet une définition précise en physique. De plus, les lois de la mécanique peuvent être liées à l’énergie grâce au théorème du travail et de l’énergie. Un coup de pied dans un ballon de football, ou tout autre exemple similaire, illustre l’idée que l’énergie cinétique d’un objet peut être augmentée par l’application d’une force. Le théorème du travail et de l’énergie, qui est une généralisation de cette idée, peut être énoncé grossièrement comme suit : La variation de l’énergie que possède un objet est égale à la magnitude de la force qui agit sur lui, multipliée par la distance à travers laquelle la force agit.
Le changement d’énergie qui se produit dans un système à la suite d’un travail peut être positif ou négatif, du point de vue du système. Le travail peut être effectué par un système, ou un système peut avoir un travail effectué sur lui par l’environnement. Si un système effectue un travail, il perd de l’énergie au profit de l’environnement. Si le système subit un travail, l’énergie du système augmente. Par exemple, lorsqu’une étincelle déclenchant un mélange de combustion dans un cylindre avec un piston mobile provoque une expansion rapide du système, et que l’expansion est mécaniquement couplée au mouvement d’une tige dans l’environnement, le système du cylindre effectue un travail sur l’environnement et, ce faisant, perd de l’énergie. C’est bien sûr une partie de la façon dont un moteur à combustion interne convertit l’énergie potentielle chimique en énergie cinétique d’une voiture en mouvement.
Une implication du théorème travail-énergie concerne les unités, à savoir que le travail peut être mesuré dans les mêmes unités que l’énergie. Puisque la deuxième loi de Newton est force = masse × accélération, le newton (N), l’unité SI pour la force, est dérivé comme M × L × T -2, et donc 1 N = 1 kg m s-2. La force multipliée par la distance a pour quantité M × L2 × T -2, et donc l’unité SI pour l’énergie, le joule (J), est définie comme 1 J = 1 kg m2 s-2. À ce stade, vous devez vérifier par vous-même que l’équation de l’énergie cinétique implique la même combinaison des quantités fondamentales que sont la masse (M), la longueur (ou distance, L) , et le temps (T).
Chaleur et température
Nous utilisons les mots chaleur et température assez fréquemment, et nous parlons souvent de la chaleur comme d’une forme d’énergie. Nous avons tous un sens intuitif de ce que sont ces choses, mais ici nous voulons y réfléchir de manière plus scientifique, et leur donner des définitions plus formelles si nous le pouvons. Il s’agit d’un prélude nécessaire à la quantification de l’énergie correspondant à la chaleur, et donc à des mesures permettant de vérifier la loi de conservation de l’énergie. Nous constatons que l’énergie thermique d’un système peut être assimilée à l’énergie cinétique totale (telle que définie ci-dessus) des atomes et molécules qui le composent. La température d’un objet ou d’un système est en fait une mesure de l’énergie cinétique moyenne des atomes et/ou molécules qui le composent. (N.B. La température n’est pas exactement égale à l’énergie cinétique moyenne des molécules, mais elle lui est directement proportionnelle. Pour plus de détails, voir la page web de la théorie cinétique moléculaire).
Une façon de visualiser ce que nous entendons par chaleur et température, et la distinction entre eux, est de considérer une analogie avec une boule de billard. Dans certains contextes simples, le comportement des boules de billard est un modèle adéquat pour une collection d’atomes ou de molécules, comme dans un échantillon d’un gaz. Tout comme les boules de billard qui viennent d’être frappées par une boule de billard en mouvement rapide, les molécules d’un gaz se déplacent dans tous les sens, rebondissant les unes sur les autres et sur les parois du récipient qui les contient. L’énergie cinétique totale des boules de billard, qui n’est que la somme des énergies cinétiques individuelles de chaque boule, est analogue au contenu en énergie thermique d’un échantillon de molécules de gaz. Lors d’une « pause » au début d’une partie de billard, l’énergie cinétique initiale de la bille blanche est répartie entre toutes les billes de la table. Certaines se déplacent assez rapidement, d’autres moins, mais l’analogie avec la « chaleur » ou l' »énergie thermique » pour le système de boules de billard est juste la somme de ces énergies cinétiques. D’autre part, la température du système de boules de billard serait proportionnelle à l’énergie cinétique moyenne de l’ensemble des boules.
Énergie potentielle électrostatique
La loi d’attraction et de répulsion électrostatique, ou loi de Coulomb, décrit la force exercée sur un objet chargé du fait de la présence d’un autre objet chargé. La force est plus facilement calculée lorsque les charges peuvent être traitées comme de très petites charges ponctuelles. L’ampleur de la force qu’un objet chargé « ressent » est proportionnelle au produit des charges (l’unité SI pour la charge électrique est le Coulomb, C), et inversement proportionnelle au carré de la distance de séparation entre les charges (r dans la figure de droite). La force est une force attractive (comme la gravité, et indiquée par des pointes de flèches dirigées vers l’intérieur dans la figure) si les charges sont de signe opposé, et répulsive lorsque les charges sont de même signe.
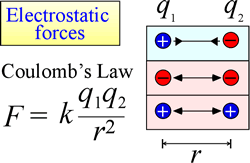
Lorsque la force (comme les forces électrostatiques, magnétiques et gravitationnelles) peut agir à distance (à travers l’espace, sans contact mécanique), on dit que les objets soumis à ces forces sont dans un champ d’énergie potentielle. Nous avons parlé plus haut de l’énergie potentielle gravitationnelle, et de même dans le cas des forces électrostatiques, un objet chargé aura une énergie potentielle électrostatique en vertu de sa position dans un champ électrique. Un tel champ existe au voisinage de toute autre charge ou charges.
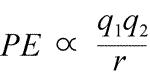
Equation de l’énergie potentielle électrostatique : PE est proportionnelle aux charges q1 et q2, et inversement proportionnelle à la distance de séparation, r. La forme de la fonction d’énergie potentielle découle mathématiquement de l’expression de la force, la loi de Coulomb.
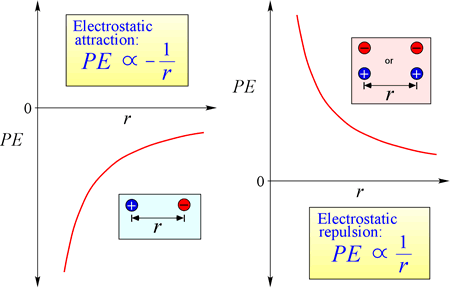
Vu les signes opposés des charges en attraction, l’énergie potentielle est toujours négative, et plus les charges se rapprochent, plus l’énergie potentielle devient négative – c’est-à-dire plus faible. Lorsque la distance de séparation, r, s’approche de zéro, l’énergie potentielle devient infiniment négative. Pour des charges de même signe, l’énergie de répulsion est toujours positive, et devient infiniment positive lorsque la distance de séparation, r, approche de zéro.
L’énergie potentielle électrostatique est une considération importante en chimie. La compréhension de la nature de l’atome, de la liaison chimique et des forces intermoléculaires dépend absolument de la prise en compte de l’influence des interactions charge-charge qui contribuent à l’énergie d’un système.
Unités importantes
Énergie (unité SI) 1 joule = 1 J = 1 kg-m-s-2
Charge élémentaire, e = 1,60218 × 10-19 C (coulomb, C)
Constante de Faraday : F = NAe = 9,64853 × 104 C-mol-1
Potentiel électrique : volts, V 1 V = 1 J C-1
.