Il n’est pas fréquent qu’une équation mathématique fasse la presse nationale, encore moins la radio populaire, ou, plus étonnant encore, fasse l’objet d’un débat au parlement britannique. Cependant, en 2003, la bonne vieille équation quadratique, que nous avons tous apprise à l’école, était tout cela.
Là où nous commençons

Tout a commencé lors d’une réunion du syndicat national des enseignants. L’équation quadratique était brandie à la nation comme un exemple de la torture cruelle infligée par les mathématiciens à de pauvres écoliers sans méfiance. Intriguée par cette accusation, l’équation quadratique a accepté un rôle de vedette à la radio aux heures de grande écoute, où elle a été interrogée par un redoutable intervieweur plus habitué à s’attaquer au Premier ministre. Le Times (de Londres) a pris de la place dans sa colonne de tête, habituellement réservée aux discussions de poids sur la santé morale (ou non) du monde moderne, pour proclamer que l’équation quadratique était inutile, que les mathématiques étaient inutiles et que personne ne voulait les étudier de toute façon, alors pourquoi s’en préoccuper ? Préoccupé par le fait que les admissions dangereuses de l’équation quadratique restent incontestées, l’importance vitale de l’équation pour la survie du Royaume-Uni a été débattue (un point de vue positif a été adopté, vous serez peut-être heureux de le savoir) à la Chambre des communes britannique.
Où tout cela allait-il s’arrêter ? L’équation quadratique était-elle vraiment morte ? Quelqu’un s’en souciait-il ? Les mathématiciens sont-ils vraiment des monstres maléfiques qui ne veulent infliger des équations quadratiques à une jeune génération que pour corrompre leurs âmes immortelles ?
Peut-être, mais ce n’est pas vraiment la faute de l’équation quadratique. En fait, l’équation quadratique a joué un rôle central non seulement dans l’ensemble de la civilisation humaine telle que nous la connaissons, mais aussi dans la détection possible d’autres civilisations extraterrestres et même dans des activités modernes aussi vitales que regarder la télévision par satellite. Quoi d’autre, en dehors de la nature de la révélation divine, pourrait être considéré comme ayant eu un tel impact sur la vie telle que nous la connaissons ? En effet, dans un sens très réel, les équations quadratiques peuvent vous sauver la vie.
Les Babyloniens
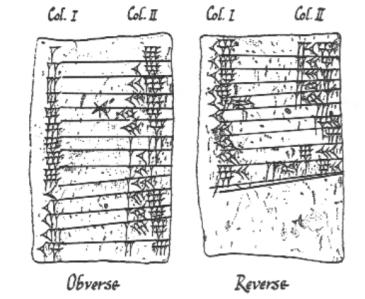
Tablettes cunéiformes babyloniennes enregistrant les 9 tables de temps
Tout a commencé vers 3000 avant JC avec les Babyloniens. Ils étaient l’une des premières civilisations du monde et ont eu de grandes idées comme l’agriculture, l’irrigation et l’écriture. Ils traçaient les trajectoires du Soleil, de la Lune et des planètes et les consignaient sur des tablettes d’argile (que l’on peut encore voir au British Museum). C’est aux Babyloniens que nous devons les idées modernes d’angle, y compris la façon dont le cercle est divisé en 360 degrés (en raison d’une petite erreur de calcul, un par jour). Nous devons également aux Babyloniens l’invention moins agréable du (redouté) percepteur. Et c’est l’une des raisons pour lesquelles les Babyloniens avaient besoin de résoudre des équations quadratiques.
Supposons que vous êtes un fermier babylonien. Quelque part dans votre ferme, vous avez un champ carré sur lequel vous faites pousser une certaine culture. Quelle quantité de votre culture pouvez-vous faire pousser sur ce champ ? Doublez la longueur de chaque côté du champ et vous constaterez que vous pouvez cultiver quatre fois plus qu’avant. La raison en est que la quantité de produit que vous pouvez cultiver est proportionnelle à la surface du champ, qui est elle-même proportionnelle au carré de la longueur du côté. En termes mathématiques, si  est la longueur du côté du champ,
est la longueur du côté du champ, 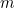 est la quantité de culture que vous pouvez faire pousser sur un champ carré de longueur latérale 1, et
est la quantité de culture que vous pouvez faire pousser sur un champ carré de longueur latérale 1, et  est la quantité de culture que vous pouvez faire pousser, alors
est la quantité de culture que vous pouvez faire pousser, alors
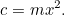 |
C’est notre première équation quadratique, nue et clignotante dans la lumière du soleil. Les équations quadratiques et les aires sont liées entre elles comme les frères et sœurs d’une même famille. Cependant, pour l’instant, nous n’avons pas à résoudre quoi que ce soit – jusqu’à ce que le percepteur arrive, bien sûr ! Il dit joyeusement au fermier : « Je veux que tu me donnes des récoltes pour payer les taxes sur ta ferme. » Le fermier est maintenant confronté à un dilemme : de quelle taille de champ a-t-il besoin pour faire pousser cette quantité de récolte ? Nous pouvons répondre à cette question facilement, en fait
récoltes pour payer les taxes sur ta ferme. » Le fermier est maintenant confronté à un dilemme : de quelle taille de champ a-t-il besoin pour faire pousser cette quantité de récolte ? Nous pouvons répondre à cette question facilement, en fait
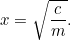 |
Faire des racines carrées en utilisant une calculatrice est facile pour nous, mais était plus un problème pour les Babyloniens. En fait, ils ont développé une méthode d’approximation successive de la réponse qui est identique à l’algorithme (appelé méthode Newton-Raphson) utilisé par les ordinateurs modernes pour résoudre des problèmes bien plus difficiles que les équations quadratiques.
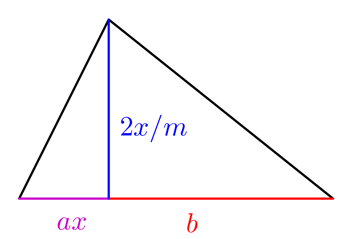
Or, tous les champs ne sont pas carrés. Supposons maintenant que l’agriculteur a un champ de forme plus étrange avec deux sections triangulaires comme indiqué sur la droite.
Pour des valeurs appropriées de  et
et 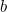 , la quantité de récolte que le fermier peut faire pousser dans ce champ est donnée par
, la quantité de récolte que le fermier peut faire pousser dans ce champ est donnée par
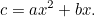 |
Cela ressemble beaucoup plus à l’équation quadratique à laquelle nous sommes habitués, et même sous le mauvais œil du fisc, c’est beaucoup plus difficile à résoudre. Pourtant, les Babyloniens ont encore trouvé la réponse. D’abord nous divisons par  pour donner
pour donner
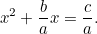 |
Maintenant nous complétons le carré en utilisant le fait que
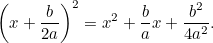 |
En combinant cela avec l’équation initiale, nous avons
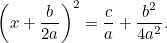 |
C’est maintenant une équation que nous pouvons résoudre en prenant des racines carrées. Le résultat est la fameuse « formule 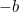 » :
» :
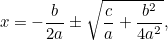 |
qui peut être réécrite comme suit
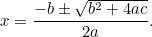 |
(La formule a généralement « -4ac » car l’équation quadratique s’écrit plus généralement sous la forme « 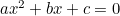 « .)
« .)
Le fait que prendre une racine carrée puisse donner une réponse positive ou négative conduit au résultat remarquable qu’une équation quadratique a deux solutions. Autant dire que les énigmes mathématiques n’ont qu’une seule solution !
Maintenant, c’est là que l’enseignement des équations quadratiques s’arrête souvent. Nous avons atteint cet objet adoré de tous les journalistes lorsqu’ils interviewent des mathématiciens – une formule. On peut inventer des questions sans fin qui consistent à mettre des valeurs de 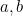 et
et  dans la formule pour donner (deux) réponses. Mais ce n’est pas du tout le but des mathématiques. Trouver une formule n’est que la première étape d’un long chemin. Nous devons nous demander ce que signifie la formule, ce qu’elle nous apprend sur l’univers, si le fait d’avoir une formule est vraiment important. Voyons maintenant où cette formule va nous mener.
dans la formule pour donner (deux) réponses. Mais ce n’est pas du tout le but des mathématiques. Trouver une formule n’est que la première étape d’un long chemin. Nous devons nous demander ce que signifie la formule, ce qu’elle nous apprend sur l’univers, si le fait d’avoir une formule est vraiment important. Voyons maintenant où cette formule va nous mener.
Une surprise pour les Grecs, un peu d’origami mathématique et un sens des proportions
Nous avançons maintenant rapidement de 1000 ans vers les Grecs anciens et voyons ce qu’ils ont fait des équations quadratiques. Les Grecs étaient de superbes mathématiciens et ont découvert une grande partie des mathématiques que nous utilisons encore aujourd’hui. L’une des équations qu’ils souhaitaient résoudre était l’équation quadratique (simple)
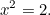 |

Ils savaient que cette équation avait une solution. En effet, c’est la longueur de l’hypoténuse d’un triangle rectangle qui avait des côtés de longueur un.
Il découle du théorème de Pythagore que si un triangle rectangle-angulaire a des côtés courts  et
et  et une hypoténuse
et une hypoténuse  alors
alors
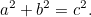 |
En mettant 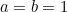 et
et  alors
alors 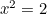 . Donc
. Donc 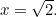
Donc, qu’est ce que  dans ce cas ? Ou, pour poser la question que posaient les Grecs, quelle sorte de nombre est-ce ? La raison pour laquelle cela importait réside dans le sens des proportions des Grecs. Ils pensaient que tous les nombres étaient proportionnels les uns aux autres. Pour être précis, cela signifie que tous les nombres étaient des fractions de la forme
dans ce cas ? Ou, pour poser la question que posaient les Grecs, quelle sorte de nombre est-ce ? La raison pour laquelle cela importait réside dans le sens des proportions des Grecs. Ils pensaient que tous les nombres étaient proportionnels les uns aux autres. Pour être précis, cela signifie que tous les nombres étaient des fractions de la forme 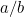 où
où  et
et  sont des nombres entiers. Des nombres comme 1/2, 3/4 et 355/113 sont tous des exemples de fractions. Il était naturel de s’attendre à ce que
sont des nombres entiers. Des nombres comme 1/2, 3/4 et 355/113 sont tous des exemples de fractions. Il était naturel de s’attendre à ce que  soit aussi une fraction. L’énorme surprise a été de constater que ce n’est pas le cas. En fait
soit aussi une fraction. L’énorme surprise a été de constater que ce n’est pas le cas. En fait
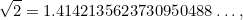 |
où les points  signifient que l’expansion décimale de
signifient que l’expansion décimale de  se poursuit à l’infini sans aucun schéma discernable. (Nous rencontrerons à nouveau cette situation plus tard lorsque nous apprendrons le chaos.)
se poursuit à l’infini sans aucun schéma discernable. (Nous rencontrerons à nouveau cette situation plus tard lorsque nous apprendrons le chaos.)
 a été le premier nombre irrationnel (c’est-à-dire un nombre qui n’est pas une fraction, ou rationnel), à être reconnu comme tel. D’autres exemples incluent
a été le premier nombre irrationnel (c’est-à-dire un nombre qui n’est pas une fraction, ou rationnel), à être reconnu comme tel. D’autres exemples incluent 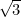 ,
,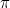 ,
,  et en fait « la plupart » des nombres. Il a fallu attendre le 19e siècle pour avoir une bonne façon de penser à ces nombres. La découverte que
et en fait « la plupart » des nombres. Il a fallu attendre le 19e siècle pour avoir une bonne façon de penser à ces nombres. La découverte que  n’était pas un nombre rationnel a provoqué à la fois une grande excitation (100 bœufs ont été sacrifiés à la suite de cette découverte) et un grand choc, le découvreur ayant dû se suicider. (Que cela soit un terrible avertissement pour les passionnés de mathématiques !) C’est à ce moment-là que les Grecs ont abandonné l’algèbre pour se tourner vers la géométrie.
n’était pas un nombre rationnel a provoqué à la fois une grande excitation (100 bœufs ont été sacrifiés à la suite de cette découverte) et un grand choc, le découvreur ayant dû se suicider. (Que cela soit un terrible avertissement pour les passionnés de mathématiques !) C’est à ce moment-là que les Grecs ont abandonné l’algèbre pour se tourner vers la géométrie.
Loin d’être un nombre obscur, nous rencontrons  régulièrement : chaque fois que nous utilisons une feuille de papier A4. En Europe, les formats de papier sont mesurés en formats A, A0 étant le plus grand avec une surface de
régulièrement : chaque fois que nous utilisons une feuille de papier A4. En Europe, les formats de papier sont mesurés en formats A, A0 étant le plus grand avec une surface de 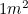 . Les formats A ont une relation particulière entre eux. Si nous faisons maintenant un peu d’origami, en prenant une feuille de papier A1 et en la pliant en deux (sur son côté le plus long), nous obtenons du papier A2. En la pliant à nouveau en deux, on obtient du A3, puis du A4, etc. Cependant, le papier est conçu de manière à ce que les proportions de chacune des tailles A soient les mêmes – c’est-à-dire que chaque morceau de papier a la même forme.
. Les formats A ont une relation particulière entre eux. Si nous faisons maintenant un peu d’origami, en prenant une feuille de papier A1 et en la pliant en deux (sur son côté le plus long), nous obtenons du papier A2. En la pliant à nouveau en deux, on obtient du A3, puis du A4, etc. Cependant, le papier est conçu de manière à ce que les proportions de chacune des tailles A soient les mêmes – c’est-à-dire que chaque morceau de papier a la même forme.
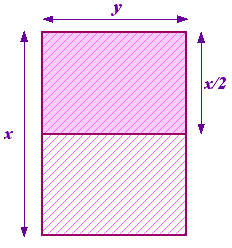
Nous pouvons poser la question de savoir de quelle proportion il s’agit. Commencez par une feuille de papier avec des côtés x et y, x étant le côté le plus long. Divisez-la ensuite en deux pour obtenir une autre feuille de papier avec des côtés y et x/2, y étant maintenant le côté le plus long. Ceci est illustré à droite.
Les proportions du premier morceau de papier sont 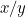 et celles du second sont
et celles du second sont 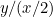 ou
ou 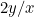 . On veut que ces deux proportions soient égales. Cela signifie que
. On veut que ces deux proportions soient égales. Cela signifie que
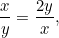 |
ou
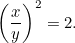 |
Encore une équation quadratique ! Heureusement, c’en est une que nous avons déjà rencontrée. En la résolvant, nous trouvons que
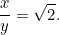 |
Ce résultat est facile à vérifier pour vous. Il suffit de prendre une feuille de papier A4 (ou A3 ou A5) et d’en mesurer les côtés. On peut aussi calculer la taille de chaque feuille. L’aire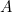 d’une feuille de papier A0 est donnée par
d’une feuille de papier A0 est donnée par
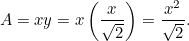 |
Mais nous savons que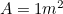 donc nous avons une autre équation quadratique pour le plus long côté
donc nous avons une autre équation quadratique pour le plus long côté
 de A0, donnée par
de A0, donnée par
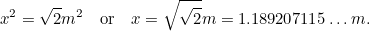 |
Cela signifie que le plus grand côté de A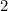 est donné par
est donné par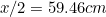 (pourquoi ?) et celui de A
(pourquoi ?) et celui de A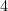 par
par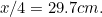 . Vérifiez ces résultats sur vos propres feuilles de papier.
. Vérifiez ces résultats sur vos propres feuilles de papier.
Le papier utilisé aux États-Unis, appelé foolscap, a une proportion différente. Pour voir pourquoi, nous retournons chez les Grecs et une autre équation quadratique. Après avoir causé tant de chagrin, l’équation quadratique se rachète dans la recherche des proportions parfaites : une recherche qui se poursuit aujourd’hui dans la conception des décors de films, et que l’on peut observer dans de nombreux aspects de la nature.
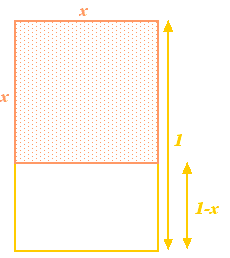
Partons d’un rectangle, puis retirons de celui-ci un carré ayant la même longueur de côté que le côté le plus court du rectangle. Si le côté le plus long du rectangle a pour longueur 1 et le côté le plus court a pour longueur  , alors le carré a des côtés de longueur
, alors le carré a des côtés de longueur  . En le retirant du rectangle, on obtient un rectangle plus petit avec le côté le plus long
. En le retirant du rectangle, on obtient un rectangle plus petit avec le côté le plus long  et le côté le plus petit
et le côté le plus petit 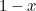 . Jusqu’ici, c’est abstrait. Cependant, les Grecs pensaient que le rectangle qui avait les proportions les plus esthétiques (le fameux rectangle d’or) était celui pour lequel le grand et le petit rectangles construits ci-dessus avaient les mêmes proportions. Pour que cela soit possible, nous devons avoir
. Jusqu’ici, c’est abstrait. Cependant, les Grecs pensaient que le rectangle qui avait les proportions les plus esthétiques (le fameux rectangle d’or) était celui pour lequel le grand et le petit rectangles construits ci-dessus avaient les mêmes proportions. Pour que cela soit possible, nous devons avoir
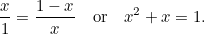 |
C’est encore une autre équation quadratique : une équation très importante qui apparaît dans toutes sortes d’applications. Elle a pour solution (positive)
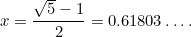 |
Le nombre  est appelé le nombre d’or et est souvent désigné par la lettre grecque
est appelé le nombre d’or et est souvent désigné par la lettre grecque 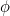 .
.

Le rectangle d’or peut être vu dans la forme des fenêtres, notamment sur les maisons géorgiennes. Plus récemment, le rapport d’or peut également être trouvé comme « forme parfaite » pour les photographies et les images de film. L’équation quadratique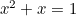 apparaît également dans les études sur les populations de lapins et dans le schéma de disposition des graines de tournesol et des feuilles sur les tiges des plantes. Tous ces éléments sont liés au nombre d’or par la séquence de Fibonacci, qui est donnée par
apparaît également dans les études sur les populations de lapins et dans le schéma de disposition des graines de tournesol et des feuilles sur les tiges des plantes. Tous ces éléments sont liés au nombre d’or par la séquence de Fibonacci, qui est donnée par
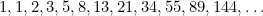 |

Graines de tournesol, disposées selon les nombres de Fibonacci |
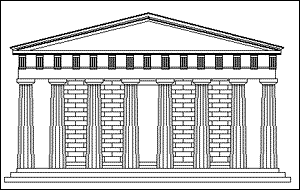
Le Parthénon, incarnant le nombre d’or |
Dans cette suite, chaque terme est la somme des deux précédents. Fibonacci l’a découvert au 15e siècle en tentant de prédire la future population de lapins. Si vous prenez le rapport de chaque terme sur celui qui le suit, vous obtenez la séquence de nombres
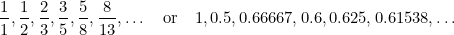 |
et ces nombres se rapprochent de plus en plus (vous l’avez deviné) du nombre d’or 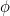 .
.
En trouvant les deux racines de l’équation quadratique ci-dessus, nous pouvons en fait trouver une formule pour le nième terme de la séquence de Fibonacci. Si  est le
est le 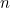 ème nombre de ce type avec
ème nombre de ce type avec 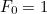 et
et 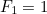 , alors
, alors  est donné par la formule
est donné par la formule
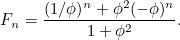 |
Les coniques relient les équations quadratiques aux étoiles

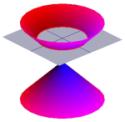
Les Grecs étaient également très intéressés par la forme des cônes. l’image de gauche montre un cône typique.
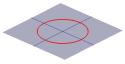
La moitié du cône peut être visualisée comme la diffusion de la lumière provenant d’une torche. Maintenant, si vous éclairez une torche sur une surface plane comme un mur, alors vous verrez différentes formes lorsque vous déplacez la torche. Ces formes sont appelées sections coniques et sont les courbes que vous obtenez si vous faites une coupe à travers un cône à différents angles. Ce sont précisément ces courbes qui ont été étudiées par les Grecs, et ils ont reconnu qu’il existait fondamentalement quatre types de sections coniques. Si vous prenez une section horizontale à travers le cône, vous obtenez un cercle. Une section faisant un petit angle avec l’horizontale donne une ellipse. Si vous prenez une section verticale, vous obtenez une hyperbole et si vous prenez une section parallèle à un côté du cône, vous obtenez une parabole. Ces courbes sont illustrées ci-dessous.
 |
 |
 |
 |
 |
 |
 |
 |

Une section transversaled’un cône peut être un cercle … |

… une ellipse … |
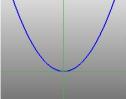
… une parabole … |
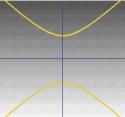
…. ou une hyperbole. |
Les sections toniques entrent dans notre histoire parce que chacune d’entre elles est décrite par une équation quadratique. En particulier, si 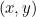 représente un point de chaque courbe, alors une équation quadratique relie
représente un point de chaque courbe, alors une équation quadratique relie  et
et 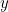 . On a :
. On a :
Le cercle : 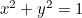 ;
;
L’ellipse : 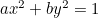 ;
;
L’hyperbole : 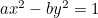 ;
;
La parabole : 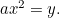
Ces courbes étaient connues et étudiées depuis les Grecs, mais à part le cercle, elles ne semblaient pas avoir d’application pratique. Cependant, comme nous le verrons dans le prochain numéro de Plus, un lien entre les équations quadratiques et les coniques, couplé à un puissant coup de chance, a permis de comprendre le fonctionnement de l’univers, et au 16ème siècle, le temps est venu pour les coniques de changer le monde.
A propos des auteurs
Chris Budd est professeur de mathématiques appliquées au département des sciences mathématiques de l’université de Bath, et titulaire de la chaire de mathématiques à la Royal Institution de Londres.
Chris Sangwin est membre du personnel de l’école de mathématiques et de statistiques de l’université de Birmingham. Il est chargé de recherche au centre du réseau de soutien à l’apprentissage et à l’enseignement pour les mathématiques, les statistiques et la recherche opérationnelle.
Ils ont récemment écrit le livre de mathématiques populaire Mathematics Galore !, publié par Oxford University Press.
Cet article a été inspiré en partie par un débat remarquable à la Chambre des communes britannique sur le sujet des équations quadratiques. Le compte rendu de ce débat se trouve dans le Hansard, Chambre des communes du Royaume-Uni, 26 juin 2003, colonnes 1259-1269, 2003, qui est disponible en ligne sur le site Web des débats du Hansard de la Chambre des communes.