Nolla

Nolla on kokonaisluku, jota merkitään numerolla 0 ja joka tarkoittaa, kun sitä käytetään laskentalukuna, että esineitä ei ole. Se on ainoa kokonaisluku (ja itse asiassa ainoa reaaliluku), joka ei ole negatiivinen eikä positiivinen. Luvun, joka ei ole nolla, sanotaan olevan ei-nolla. Funktion juurta kutsutaan joskus myös nimellä ”:n nolla.”

Schoolhouse Rockin kappaleessa ”My Hero, Zero” ylistetään nollan hyvyyttä muun muassa seuraavilla ylistyslauseilla: ”My hero, zero Sellainen hassu pikku sankari Mutta ennen kuin sinä ilmestyit Me laskimme sormillamme ja varpaillamme Nyt olet täällä jäädäksemme Ja kukaan ei oikeastaan tiedä Kuinka ihana olet Miksi emme koskaan yltäisi tähdelle Ilman sinua, nolla, sankarini Kuinka ihana olet.”

Nollaa pidetään yleisesti tekijöinä (esim, Wolfram-kielen FactorInteger-komennossa). Toisaalta divisorit ja divisori-funktio otetaan yleisesti määrittelemättömiksi, koska sopimuksen mukaan (eli jakaa 0:n) jokaiselle :lle paitsi nollalle.”

Koska 0-alkioiden permutaatioiden lukumäärä on 1, (nollan faktoriaalin) määrittelyssä käytetään arvoa 1 (Wells 1986, s. 31). Tämä määritelmä on hyödyllinen ilmaistessa monia matemaattisia identiteettejä yksinkertaisessa muodossa.

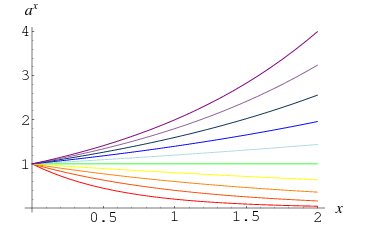
Muu luku kuin 0 potenssiin 0 otettuna määritellään olevan 1, mikä seuraa raja-arvosta

Tätäkin tosiasiaa havainnollistaa käppyröiden konvergenssi pisteessä ylläolevassa kaaviokuvassa, joka osoittaa :aa :llä :lle :lle 0:aa.4, …, 2.0. Se voidaan nähdä myös intuitiivisemmin huomaamalla, että toistuva luvun neliöjuuren ottaminen antaa yhä pienempiä ja pienempiä lukuja, jotka lähestyvät ykköstä ylhäältä päin, kun taas saman tekeminen luvulla 0:n ja 1:n välillä antaa yhä suurempia ja suurempia lukuja, jotka lähestyvät ykköstä alhaalta päin. Kun neliöjuuret otetaan yhteensä , joka lähestyy 0:ta, kun on suuri, jolloin saadaan siinä raja-arvossa, että on suuri.

itsessään on määrittelemätön. Tämän suureen tarkkaan määritellyn merkityksen puute seuraa keskenään ristiriitaisista tosiasioista, että on aina 1, joten :n pitäisi olla 1, mutta on aina 0 (:lle), joten :n pitäisi olla 0. Voidaan väittää, että on luonnollinen määritelmä, koska

Mutta raja-arvoa ei ole olemassa yleisille kompleksisille -arvoille. Siksi :n määritelmän valinta määritellään yleensä epämääräiseksi.

Mutta :n määrittely mahdollistaa joidenkin kaavojen ilmaisemisen yksinkertaisesti (Knuth 1992; Knuth 1997, s. 57), joista esimerkkinä on Koganin (vrt. Espinosa ja Moll 2000) antama kaunis analyyttinen kaava yleistetyn sinifunktion integraalille

, jossa , ja on lattian funktio.

Richardsonin lause on ratkaisukelpoisuusteorian perustavaa laatua oleva tulos, joka osoittaa, että sen määrittäminen, ovatko yksinkertaisetkin lausekkeet identtisesti nollan kanssa yhtä suuria, on periaatteessa ratkaisukelvotonta, saati sitten käytännössä.

Seuraavassa taulukossa annetaan ensimmäiset sellaiset luvut , joilla :n desimaalilaajennus ei sisällä nollia pienille :lle (ongelma muistuttaa Gelfandin kysymystä.) Suurin tunnettu , jolle ei sisällä nollia, on 86 (Madachy 1979), muita ei ole (M. Cook, henkilökohtainen tiedonanto), 26.9.1997 ja 16.3.1998), mikä parantaa Beelerin ja Gosperin (1972) saamaa -rajaa. Arvot , joilla :n oikeanpuoleisimman nollan sijainti kasvaa, ovat 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, … (OEIS A031140). Paikat, joissa oikeanpuoleisimmat nollat esiintyvät, ovat 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, …. (OEIS A031141). :n oikeanpuoleisin nolla on 217:nnen desimaalin kohdalla, joka on kauimpana potensseista :een asti.

	Sloane	siten, että ei sisällä yhtään nollaa
2	A007377	1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, …
3	A030700	1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, …
4	A030701	1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, …
5	A008839	1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, …
6	A030702	1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, …
7	A030703	1, 2, 3, 6, 7, 10, 11, 19, 35
8	A030704	1, 2, 3, 5, 6, 8, 9, 8, 9, 9, 9, 9, 9, 11, 11, 12, 12, 12, 13, 13, 13, 17, 14, 24, 27
9	A030705	1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34
11	A030706	1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, …

Vaikka ei ole todistettu, että edellä luetellut luvut ovat ainoat luvut, joissa ei ole nollia tietyssä perusluvussa, todennäköisyys sille, että muita on olemassa, on häviävän pieni. Tällä oletuksella suurimpien sarja, joka on sellainen, että ei sisällä nollia luvuille , 3, …, on tällöin 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, …. (OEIS A020665).

.