Vinklen, der dannes, når radius
vinder rundt om en cirkel:
 |
1 radian er ca. 57,2958 grader. |
Hvorfor “57,2958…” grader? Det vil vi se om lidt.
Radianen er et rent mål baseret på cirklens radius:
Radian: den vinkel, der dannes, når vi tager radius
og vikler den rundt om cirklen.
Radianer og grader
Lad os se, hvorfor 1 radian er lig med 57.2958… grader:
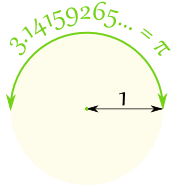
I en halvcirkel er derπ radianer, som også er 180°
For at gå fra radianer til grader: multiplicer med 180, divider med π
For at gå fra grader til radianer: multiplicer med π, divider med 180
Her er en tabel med ækvivalente værdier:
| Degrees | Radians (nøjagtig) |
Radians (ca.) |
|---|---|---|
| 30° | π/6 | 0.524 |
| 45° | π/4 | 0,785 |
| 60° | π/3 | 1.047 |
| 90° | π/2 | 1,571 |
| 180° | π | 3.142 |
| 270° | 3π/2 | 4,712 |
| 360° | 2π | 6,283 |
Eksempel: Hvor mange radianer er der i en hel cirkel?
Forestil dig, at du klipper stykker snor af, der har nøjagtig samme længde fra centrum til omkredsen af en cirkel …
… hvor mange stykker skal du bruge for at gå en gang rundt om cirklen?
Svar: 2π (eller ca. 6,283 stykker snor).
Radianer foretrukket af matematikere
Da radianen er baseret på den rene idé om, at “radius er lagt langs omkredsen”, giver den ofte enkle og naturlige resultater, når den anvendes i matematik.
Se f.eks. på sinusfunktionen for meget små værdier:

