Lad os begynde med at undersøge division af værdier med eksponenter.
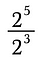
Husk, at eksponenter repræsenterer gentagen multiplikation. Så vi kan omskrive ovenstående udtryk som:
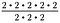
Da 2/2 = 1, annulleres tre sæt 2/2. Det efterlader 2 – 2, eller 2 i kvadrat.
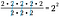
Vi kan selvfølgelig tage en genvej og trække antallet af 2’ere i bunden fra antallet af 2’ere i toppen. Da disse størrelser er repræsenteret ved deres respektive eksponenter, skal vi blot skrive den fælles base med forskellen i eksponentværdierne som potens.
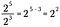
Hvis vi generaliserer denne regel, har vi følgende, hvor n repræsenterer et reelt tal, der ikke er nul, og x og y er også reelle tal.
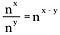
Udfordring af nulpotensen
Derfra er det let at udlede forklaringen på, hvorfor ethvert tal, der ikke er nul, og som er hævet til nulpotensen, er lig med 1. Lad os igen se på et konkret eksempel.
Vi ved, at ethvert tal, der ikke er nul, divideret med sig selv er lig med 1. Så jeg kan skrive følgende:
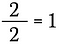
Det er det samme som at skrive:
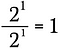
Nu vil jeg bruge eksponentreglen fra ovenfor til at omskrive venstre side af denne ligning.
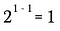
Dette svarer selvfølgelig til:
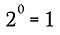
Vi kan bruge den samme fremgangsmåde som i dette eksempel, sammen med den generaliserede regel ovenfor, til at vise, at ethvert reelt tal, der ikke er nul, og som er hævet til en potens af nul, må resultere i 1.
Hvad med nul til nul potens?
Det er her, at tingene bliver vanskelige. Ovenstående metode går i stykker, fordi det naturligvis er forbudt at dividere med nul. Lad os undersøge hvorfor.
Vi begynder med at kigge på en almindelig divider med nul FEJL.
Hvad med 2÷0? Lad os se på, hvorfor vi ikke kan gøre dette.
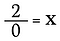
Division er egentlig bare en form for multiplikation, så hvad sker der, hvis jeg omskriver ovenstående ligning som:
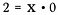
Hvilken værdi kunne muligvis tilfredsstille denne ligning for x?
Der findes ingen værdi! Ethvert tal gange nul resulterer i nul, det kan aldrig blive lig med 2. Derfor siger vi, at division med nul er udefineret. Der er ingen mulig løsning.
Lad os nu se på 0÷0.
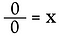
Også her skal vi omskrive det som et multiplikationsproblem.
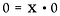
Her støder vi på en meget anderledes situation. Løsningen for x kunne være et hvilket som helst reelt tal! Der er ingen måde at bestemme, hvad x er. Derfor betragtes 0/0 som ubestemt*, ikke som ubestemt.
Hvis vi forsøger at bruge ovenstående metode med nul som base til at bestemme, hvad nul til nul potens ville være, går vi straks i stå og kan ikke fortsætte, fordi vi ved, at 0÷0 ≠ 1, men er ubestemt.
Så hvad er nul til nul potens lig med?
Dette er meget omdiskuteret. Nogle mener, at det skal defineres som 1, mens andre mener, at det er 0, og nogle mener, at det er ubestemt. Der er gode matematiske argumenter for hver af dem, og måske er det mest korrekt at betragte det som ubestemt.
På trods af dette går det matematiske samfund ind for at definere nul til nul potens som 1, i det mindste til de fleste formål.
Men måske er en nyttig definition af eksponenter for amatørmatematikeren følgende: