Matematisk modellering

by admin Leave Comment

Læringsmål

  • Indledning til stykkevis lineære funktioner
    • Definition af stykkevis lineære funktioner funktion
    • Evaluere en stykkevis funktion
    • Skriv en stykkevis funktion givet en anvendelse
  • Grafering af stykkevise funktioner
    • Givet en stykkevis-defineret funktion, skitsér en graf
    • Skriv domæne og område for en stykkevis defineret funktion givet en graf

Nogle funktioner kommer i stykker. I dette afsnit vil vi lære om, hvordan man definerer og graferer funktioner, der i det væsentlige er samlinger af diskrete stykker. Eksempler på noget, der er defineret på denne måde, omfatter udformning af en bils profil, udregning af dit mobilabonnement og beregning af indkomstskattesatser. F.eks. afhænger din skattesats af din indkomst og er den samme for en række forskellige indkomster, som det fremgår af nedenstående tabel:

Marginalskattesats Single skattepligtig indkomst Gifte, der indgiver fælles indkomstanmeldelse eller kvalificeret enke(er) skattepligtig Income Married Filing Separately Taxable Income Head of Household Taxable Income
10% $0 – $9,275 $0 – $18,550 $0 – $9,275 $0 – $13,250
15% $9,276 – $37,650 $18,551 – $75,300 $9,276 – $37,650 $13,251 – $50,400
25% $37,651 – $91,150 $75,301 – $151,900 $37,651 – $75,950 $50,401 – $130,150
28% $91,151 – $190,150 $151,901 – $231,450 $75,951 – $115,725 $130,151 – $210,800
33% $190,151 – $413,350 $231,451 – $413,350 $115,726 – $206,675 $210,801 – $413,350
35% $413,351 – $415,050 $413,351 – $466,950 $206,676 – $233,475 $413,351 – $441,000
39.6% $415,051+ $466,951+ $233,476+ $441,001+

En stykkevis funktion er en funktion, hvor der anvendes mere end én formel til at definere output over forskellige stykker af domænet.

Vi bruger stykkevise funktioner til at beskrive situationer, hvor en regel eller et forhold ændrer sig, når inputværdien krydser visse “grænser”. F.eks. støder vi ofte på situationer i erhvervslivet, hvor prisen pr. stk. af en bestemt vare nedsættes, når antallet af bestilte varer overstiger en bestemt værdi. Skatteklammer er et andet virkeligt eksempel på stykkevise funktioner. For eksempel kan man overveje et simpelt skattesystem, hvor indkomster op til 10 000 USD beskattes med 10 %, og hvor alle yderligere indkomster beskattes med 20 %. Skatten på en samlet indkomst, S, ville være 0,1S, hvis S\le 10.000 $ og 1000 + 0,2 (S – 10.000 $), hvis S> 10.000 $.

Stykkevis funktion

En stykkevis funktion er en funktion, hvor mere end én formel anvendes til at definere output. Hver formel har sit eget domæne, og funktionens domæne er foreningen af alle disse mindre domæner. Vi noterer denne idé således:

f\left(x\right)=\begin{cases}\text{formel 1 hvis x er i domæne 1}\\\ \text{formel 2 hvis x er i domæne 2}\\\ \text{formel 3 hvis x er i domæne 3}\end{cases}

I stykkevis notation er den absolutte værdifunktion

|x|=\begin{cases}x\text{ if }x\ge 0\\\ -x\text{ if }x<0\end{cases}

Evaluér en stykkevis defineret funktion

I det første eksempel vil vi vise, hvordan man evaluerer en stykkevis defineret funktion. Bemærk, hvordan det er vigtigt at være opmærksom på domænet for at bestemme, hvilket udtryk der skal bruges til at evaluere input.

Eksempel

Givet funktionen

f(x)=\begin{cases}7x+3\text{ if }x<0\\\7x+6\text{ if }x\ge{0}\end{cases},

evaluere:

  1. f (-1)
  2. f (0)
  3. f (2)
Vis svar

1.f(x) er defineret som 7x+3 for x=-1\text{ becuase }-1<0.

Vurder: f(-1)=7(-1)+3=-7+3=-4

2. f(x) er defineret som 7x+6 for x=0\text{ becuase }0\ge{0}.

Vurder: f(0)=7(0)+6=0=0+6=6

3. f(x) er defineret som 7x+6 for x=2\text{ becuase }2\ge{0}.

Vurder: f(2)=7(2)+6=14+6=20

I den følgende video viser vi, hvordan man kan vurdere flere værdier givet en stykkevis defineret funktion.

I det næste eksempel viser vi, hvordan man evaluerer en funktion, der modellerer omkostningerne ved dataoverførsel for et telefonselskab.

Eksempel

Et mobiltelefonselskab bruger nedenstående funktion til at bestemme omkostningerne, C, i dollars for g gigabyte dataoverførsel.

C\left(g\right)=\begin{cases}{25}\text{ if }{ 0 }<{ g }<{ 2 }\\\ 10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

Find omkostningerne ved at bruge 1.5 gigabyte data og omkostningerne ved at bruge 4 gigabyte data.

Vis svar

For at finde omkostningerne ved at bruge 1,5 gigabyte data, C(1,5), skal vi først se, hvilken del af domænet vores input falder i. Da 1,5 er mindre end 2, bruger vi den første formel.

C(1,5) = 25 $

For at finde omkostningerne ved at bruge 4 gigabyte data, C(4), ser vi, at vores input på 4 er større end 2, så vi bruger den anden formel.

C(4)=10(4)+5=45

Analyse af løsningen

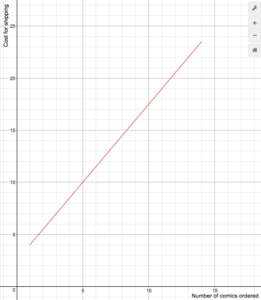
Funktionen er repræsenteret i nedenstående graf. Vi kan se, hvor funktionen overgår fra en konstant til en linje med en positiv hældning ved g=2. Vi plotter graferne for de forskellige formler på et fælles sæt akser, idet vi sikrer os, at hver formel anvendes på sit rette område.

C(g) = C\left(g\right)=\begin{cases}{25}\text{ if }{ 0 }<{ g }<{ 2 }\\\ 10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

Skriv en stykkevis defineret funktion

I det sidste eksempel vil vi vise, hvordan man skriver en stykkevis defineret funktion, der modellerer prisen på en guidet museumsrundvisning.

Eksempel

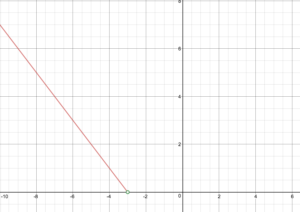
Et museum tager 5 $ pr. person for en guidet rundvisning med en gruppe på 1-9 personer eller et fast gebyr på 50 $ for en gruppe på 10 eller flere personer. Skriv en funktion, der relaterer antallet af personer, n, til prisen, C.

Vis svar

Der vil være behov for to forskellige formler. For n-værdier under 10 er C=5n. For n-værdier på 10 eller derover er C=50.

C(n)=\begin{cases}{5n}\text{ if }{0}<{n}<{10}\\ 50\text{ if }{n}\ge 10\end{cases}

Analyse af løsningen

Funktionen er repræsenteret i figur 21. Grafen er en diagonal linje fra n=0 til n=10 og en konstant herefter. I dette eksempel stemmer de to formler overens i mødestedet, hvor n=10, men ikke alle stykkevise funktioner har denne egenskab.

I den følgende video viser vi et eksempel på at skrive en stykkevis defineret funktion givet et scenarie.

Givet en stykkevis defineret funktion, skriv formlen og identificer domænet for hvert interval.

  1. Identificer de intervaller, for hvilke der gælder forskellige regler.
  2. Detekter formler, der beskriver, hvordan man beregner et output ud fra et input i hvert interval.
  3. Brug parenteser og if-sætninger til at skrive funktionen.

Graferer stykkevise funktioner

I dette afsnit skal vi plotte stykkevise funktioner. Funktionen, der er plottet nedenfor, repræsenterer omkostningerne ved at overføre data for et givet mobiltelefonselskab. Vi kan se, hvor funktionen skifter fra en konstant til en linje med en positiv hældning ved g=2. Når vi plotter stykkevise funktioner, er det vigtigt at sikre, at hver formel anvendes på det rigtige område.C\left(g\right)=\begin{cases}{25} \text{ if }{ 0 }<{ g }<{ 2 }\\\\10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

I dette tilfælde er output 25 for ethvert input mellem 0 og 2. For værdier lig med eller større end 2 er outputtet defineret som 10g+5.

Skitsér en graf for en stykkevis funktion.

  1. Angiv på x-aksen de grænser, der er defineret af intervallerne på hvert stykke af domænet.
  2. For hvert stykke af domænet skal du tegne en graf på det pågældende interval ved hjælp af den tilsvarende ligning, der vedrører det pågældende stykke. Man må ikke tegne en graf af to funktioner over ét interval, da det ville være i strid med kriterierne for en funktion.

Eksempel

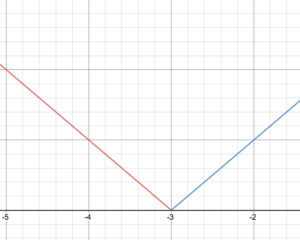
Skitsér en graf af funktionen.

Givet den stykkevise definition f(x)=\begyn{cases}-x – 3\text{ if }x < -3\\ x + 3\text{ if } x \ge -3\end{cases}
Tegn grafen for f.
Angiv funktionens domæne og område.

Vis svar

Tegn først grafen for linjen f(x) = -x-3, idet du sletter den del, hvor x er større end -3. Placer en åben cirkel i punktet (-3,0).

Placér nu linjen f(x) = x+3 på grafen, med udgangspunkt i punktet (-3,0). Bemærk, at for denne del af grafen er punktet (-3,0) medtaget, så du kan fjerne den åbne cirkel.

De to grafer mødes i punktet (-3,0)

Domænet for denne funktion er alle reelle tal, fordi (-3,0)ikke er medtaget som endepunkt for f(x) = -x-3, men det er medtaget som endepunkt for f(x) = x+3.

Det område for denne funktion starter ved f(x)=0 og omfatter 0 og går til uendelig, så vi ville skrive dette som x\ge0

I det næste eksempel skal vi tegne en stykkevis defineret funktion, der modellerer forsendelsesomkostningerne for en online tegneserieforhandler.

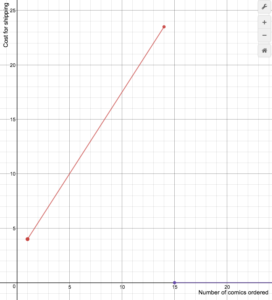
Eksempel

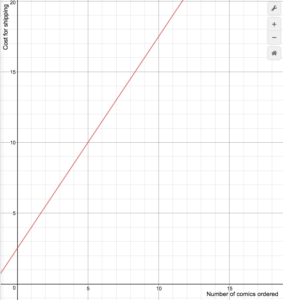
En online-tegneserieforhandler opkræver forsendelsesomkostninger i henhold til følgende formel

S(n)=\begin{cases}1,5n+2.5\text{ if }1\le{n}\le14\\\0\text{ if }n\ge15\end{cases}

Tegn en graf over omkostningsfunktionen.

Vis svar

Tegn først linjen S(n)=1,5n+2,5. Vi kan bruge transformationer: Dette er en lodret strækning af identiteten med en faktor 1,5, og en lodret forskydning med 2,5.

S(n)=1,5n+2.5

Nu kan vi fjerne de dele af grafen, der ikke er i domænet baseret på 1\le{n}\le14

S(n) = 1,5n+2,5 for 1<=n<=14

Sidst skal vi tilføje den konstante funktion S(n)=0 for indgange større end eller lig med 15. Placér lukkede prikker i grafernes ender for at angive, at endepunkterne er medtaget.

I den følgende video viser vi, hvordan man graferer en stykkevis defineret funktion, som er lineær over begge domæner.

Resumé

  • En stykkevis defineret funktion er en funktion, hvor der bruges mere end én formel til at definere output over forskellige dele af domænet.
  • Evaluering af en stykkevis defineret funktion betyder, at man skal være meget opmærksom på det korrekte udtryk, der bruges til det givne input

For at grafisere stykkevis definerede funktioner skal man først identificere, hvor domænet er delt. Grafér funktioner på domænet ved hjælp af værktøjer som f.eks. plottepunkter eller transformationer. Vær omhyggelig med at bruge åbne eller lukkede cirkler på endepunkterne af hvert domæne baseret på, om endepunktet er inkluderet.

Skriv et svar

Din e-mailadresse vil ikke blive publiceret.