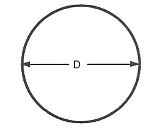
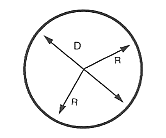
Diameter af en cirkel
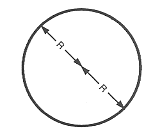
Diameteren af en cirkel eller kugle er lig med 2 gange radius.
$\text “Diameter” = 2 ⋅ \text “Radius”$

Omkreds af en cirkel
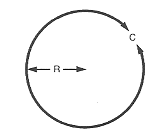
Omkredsen af en cirkel eller en kugle er lig med 6,2832 gange Radiusen.
$\text “Omkreds” = 6,2832 ⋅ R$
$C = 2 ⋅ π ⋅ R$
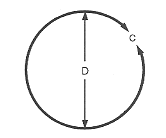
Omkredsen af en cirkel eller en kugle er lig med 3,1416 gange diameteren.
$\text “Omkreds” = 3.1416 ⋅ \text “Diameter”$
$C = π ⋅ D$
Radius af en cirkel
Radius af en cirkel eller kugle er lig med Diameter divideret med 2.
$R = D / 2$
Aareal af en cirkel
Aarealet af en cirkel er lig med cirklens radius ganget med radius og derefter dette tal ganget med 3,1416.
$\text “Areal” = R^2 ⋅ π$
$\text “Areal” = R ⋅ R ⋅ R ⋅ 3,1416$
Dette tal vil være i kvadratcentimeter eller kvadratmillimeter, afhængigt af det anvendte målesystem.
Aarealet af en cirkel er lig med cirklens diameter ganget med diameteren og derefter dette tal ganget med 3,1416 og derefter divideres denne sum med 4.
$\text “Areal” = D ⋅ D ⋅ D ⋅ 3.1416 / 4$
$\text “Area” = D^2 ⋅ π/ 4$
Area of a Cylinder
Dette tal vil være i kvadrattommer eller kvadratmillimeter, afhængigt af det anvendte målesystem.
Aarealet af en cylinder er lig med 6,2832 ( 2 × π) gange cylinderens radius gange summen af radien plus højden.
$\text “Areal” = 2 ⋅ 3.1416 ⋅ R ⋅ R ⋅ ( R + H )$
$\text “Areal” = 2 ⋅ π ⋅ R ⋅ R ⋅ ( R + H )$
Dette tal vil være i kvadratcentimeter eller kvadratmillimeter, afhængigt af det anvendte målesystem.
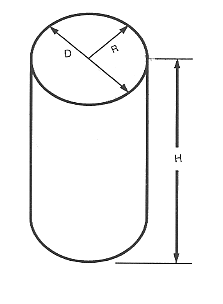
Cylinderens volumen
Cylinderens volumen er lig med cylinderens radius, ganget med radius, og dette tal ganget med 3,1416, hvorefter dette tal ganges med cylinderens længde.
$\text “Volumen” = 3.1416 ⋅ R ⋅ R ⋅ H$
$\text “Volumen” = π ⋅ R^2 ⋅ H$
Dette tal vil være i kubiktommer eller kubikmillimeter, afhængigt af det anvendte målesystem.
Aareal af en kugle
Aarealet af en kugle er lig med kvadratet på kuglens radius ganget med 12,566 ( 4 × π) eller Pi gange diameteren i kvadrat ( π × D × D ).
$tekst “Areal” = 12.566 ⋅ R ⋅ R$
$\text “Areal” = 4 ⋅ π ⋅ R^2$
$\text “Areal” = π ⋅ D^2$
Dette tal vil være i kvadratcentimeter eller kvadratmillimeter, afhængigt af det anvendte målesystem.
Volumen af en kugle
Volumen af en kugle er lig med kuglens radius, ganget med radius igen. Derefter multipliceres dette tal med radius igen. Derefter ganges dette tal med 12,566. og resultatet divideres med 3.
$\text “Volumen” = 12.566 ⋅ R ⋅ R ⋅ R ⋅ R / 3$
$\text “Volumen” = 4 ⋅ π ⋅ R ⋅ R ⋅ R ⋅ R / 3$
$\text “Kuglevolumen” = 4/3 ⋅ π ⋅ r^3 = ( π ⋅ d^3)/6$
Dette tal vil være i kubiktommer eller kubikmillimeter, afhængigt af hvilket målesystem der anvendes.