De forskellige typer styringer anvendes til at forbedre styringssystemers ydeevne. I dette kapitel vil vi diskutere de grundlæggende regulatorer såsom proportional-, aflednings- og integralregulatorer.
Proportionalregulator
Den proportionale regulator producerer et output, som er proportionalt med fejlsignalet.
$$$$u(t) \propto e(t) $$
$$$\Rightarrow u(t)=K_P e(t)$$
Anvend Laplace-transformationen på begge sider –
$$$$U(s)=K_P E(s)$$
$$$\frac{U(s)}{E(s)}=K_P$$$
Derfor, er proportionalregulatorens overførselsfunktion $K_P$.
Hvor,
U(s) er Laplace-transformationen af aktuatorsignalet u(t)
E(s) er Laplace-transformationen af fejlsignalet e(t)
KP er proportionalitetskonstanten
Blokdiagrammet for det enheds negativ tilbagekoblede reguleringssystem med lukket kredsløb sammen med den proportionale regulator er vist i følgende figur.
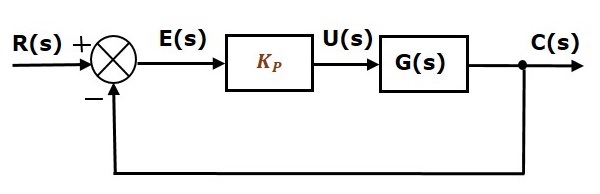
Proportionalregulatoren bruges til at ændre det transiente respons efter behov.
Derivatregulator
Den derivatregulator producerer et output, som er derivat af fejlsignalet.
$$$u(t)=K_D \frac{\text{d}e(t)}{\text{d}t}}$$$
Anvend Laplace-transformation på begge sider.
$$$U(s)=K_D sE(s)$$
$$$\frac{U(s)}{E(s)}=K_D s$$$
Dermed er overførselsfunktionen for den afledte regulator $K_D s$.
Hvor $K_D$ er den afledte konstant.
Blokdiagrammet for det lukkede reguleringssystem med negativ tilbagekobling af enheden sammen med den afledte regulator er vist i følgende figur.
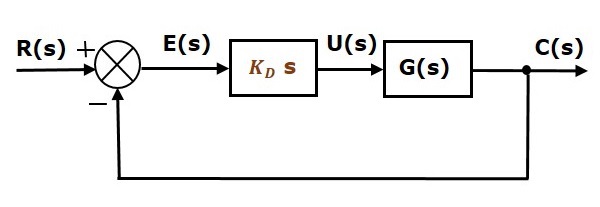
Den afledte regulator anvendes til at gøre det ustabile reguleringssystem til et stabilt system.
Integralregulator
Integralregulatoren producerer et output, som er integral af fejlsignalet.
$$$u(t)=K_I \int e(t) dt$$$
Anvend Laplace-transformation på begge sider –
$$$U(s)=\frac{K_I E(s)}{s}$$
$$$\frac{U(s)}{E(s)}=\frac{K_I}{s}$$$
Derfor, er overførselsfunktionen for den integrale regulator $\frac{K_I}{s}$.
Hvor $K_I$ er den integrale konstant.
Blokdiagrammet for det enhedsnegativ tilbagekoblede reguleringssystem med lukket kredsløb sammen med integralregulatoren er vist i følgende figur.
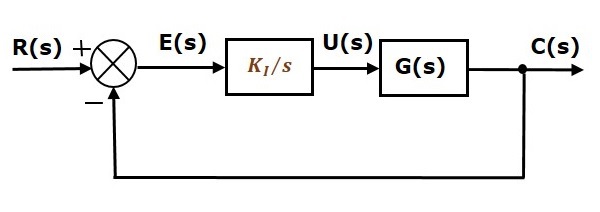
Integralregulatoren bruges til at mindske den stationære fejl.
Lad os nu diskutere kombinationen af de grundlæggende regulatorer.
Proportional-afledningsregulator (PD)
Den proportional-afledningsregulator producerer et output, som er kombinationen af udgangene fra proportional- og afledningsregulatorerne.
$$$u(t)=K_P e(t)+K_D \frac{\text{d}e(t)}{\text{d}t}}$$$$
Anvend Laplace-transformation på begge sider –
$$$$U(s)=(K_P+K_D s)E(s)$$$
$$$\frac{U(s)}{E(s)}=K_P+K_D s$$$
Derfor, er overførselsfunktionen for den proportionale afledte regulator $K_P + K_D s$.
Blokdiagrammet for det lukkede reguleringssystem med negativ tilbagekoblet enhedsregulering sammen med den proportionale afledningsregulator er vist i følgende figur.
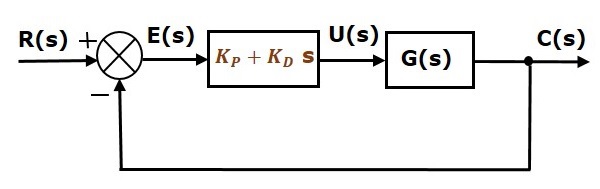
Den proportionale afledningsregulator anvendes til at forbedre stabiliteten af reguleringssystemet uden at påvirke steady state-fejlen.
Proportional Integral (PI)-regulator
Den proportionale integralregulator producerer et output, som er en kombination af output fra proportional- og integralregulatorerne.
$$$u(t)=K_P e(t)+K_I \int e(t) dt$$$
Anvend Laplace-transformation på begge sider –
$$$$U(s)=\left(K_P+\frac{K_I}{s} \right )E(s)$$
$$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}$$$
Derfor, er overførselsfunktionen for den proportionale integralregulator $K_P + \frac{K_I} {s}$.
Blokdiagrammet for det lukkede reguleringssystem med enheds negativ feedback sammen med den proportionale integralregulator er vist i følgende figur.
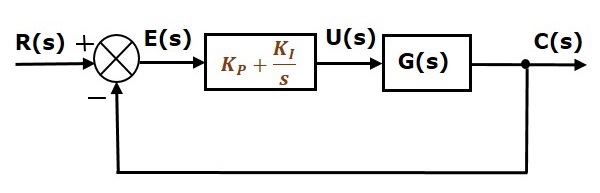
Den proportionale integralregulator anvendes til at reducere den stationære fejl uden at påvirke stabiliteten af reguleringssystemet.
Proportional Integral Derivativ (PID)-regulator
Den proportionale integral derivativregulator producerer et output, som er en kombination af udgangene fra proportional-, integral- og derivativregulatorerne.
$$$u(t)=K_P e(t)+K_I \int e(t) dt+K_D \frac{\text{d}e(t)}{\text{d}t}}$$$
Anvend Laplace-transformation på begge sider –
$$$$U(s)=\left(K_P+\frac{K_I}{s}+K_D s \right )E(s)$$
$$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}+K_D s$$$
Derfor, er overførselsfunktionen for den proportionale integralafledningsregulator $K_P + \frac{K_I} {s} + K_D s$.
Blokdiagrammet for det lukkede reguleringssystem med enheds negativ feedback sammen med den proportionale integralafledningsregulator er vist i følgende figur.
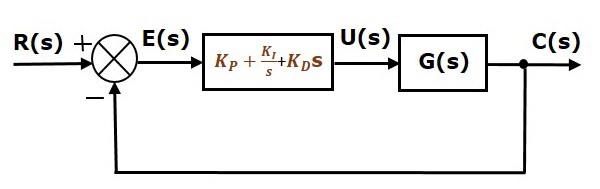
Den proportionale integralafledningsregulator anvendes til at forbedre stabiliteten af reguleringssystemet og til at mindske steady state-fejlen.