Et vigtigt spørgsmål er, hvordan er primtal fordelt blandt de hele tal? Svaret er, med ganske få ord, temmelig tilfældigt, givet visse grundlæggende statistikker …
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
E-mail Bill Casselman
| |
|
Introduktion
For mange år siden blev det formodet, at der findes et uendeligt antal par af primtal $p$, $q$ med $q = p+2$. Der er for nylig sket nogle nylige (og berømte) fremskridt med hensyn til dette problem. Jeg vil sige lidt om de seneste fremskridt, men i stedet diskutere, hvad vi forventer – snarere end hvad vi ved – om sådanne par. Intet af det, jeg vil sige, er nyt, og jeg har til en vis grad blot uddybet, hvad Andrew Granville siger i sin nylige redegørende note om de seneste fremskridt.
Hvor mange primtal forventer vi?
Et primtal er et positivt heltal, der ikke har andre divisorer end sig selv og $1$. Definitionen er enkel, men så snart man begynder at udforske betydningen af primtal, opdager man, at de udviser en meget subtil adfærd. Et vigtigt spørgsmål er, hvordan primtal er fordelt blandt de hele tal? Svaret er, med ganske få ord, temmelig tilfældigt, givet visse grundlæggende statistikker. Hvad mener jeg med dette?
Jamen, her er et kvadratisk array, der forestiller alle primtal op til $400$:

Der er nogle mønstre i dette array, hvoraf jeg senere vil kommentere nogle af dem. De fleste af dem, du opfatter, er forårsaget af en eller anden artefakt i displayet. For eksempel er hver anden kolonne stort set tom, og det skyldes, at det eneste lige primtal er $2$. Desuden er hver femte kolonne stort set tom. Mere interessante er de dobbelte primtalpar (hvoraf nogle ikke er så synlige, fordi de er delt op i to rækker, f.eks. $59$, $61$) og også nogle mønstre i forbindelse med de sidste viste cifre. Disse er det, man kunne kalde lokale mønstre. Der er ingen globale mønstre synlige.
Der er blevet brugt mange kræfter på ekstremt effektive måder at fremstille primtal på, men i dag tager selv et meget simpelt program kun lidt tid at fremstille store lister med primtal. Et af de mest frugtbare programmer vil lave en stor liste af primtal og derefter bruge denne til at beregne funktionen $\pi(n)$, antallet af primtal $\le n$.
En af de ting, dette kan bruges til, er at få en grov idé om hyppigheden af primtal. Der er $135$ primtal i intervallet $$:
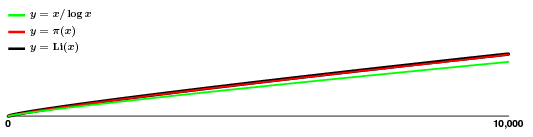
Den tilnærmelse ser godt ud! Så selv om $\pi(x)$ hopper lidt rundt, tilsyneladende uden noget mønster, har vi et ret godt estimat for det, hvilket betyder, at vi har en god idé om, hvordan primtalene vokser, i hvert fald i gennemsnit.
Det skal dog holdes for øje, at den tilsyneladende jævnhed er bedragerisk. Tæt på ser de to øverste kurver således ud:

Kommentarer?
Heuristisk ræsonnement om tvillingprimer
Twillingprimer er et par $p$, $p+2$, som begge er primer. Af et af ovenstående diagrammer fremgår f.eks. tvillingpræmierne $$ , , , , , , , , $$
og andre. Det er blevet formodet, at der er uendeligt mange af dem, men selv om der er mange empiriske beviser for dette, er det endnu ikke blevet bevist.
Det måske stærkeste bevis er en formel, der tilnærmer antallet $\pi_{2}(x)$ af tvillingprimer $\le x$ bemærkelsesværdigt godt. Jeg er ikke helt sikker på oprindelsen af denne formel, men den optrådte første gang i en artikel af G. H. Hardy og J. E. Littlewood (selv et par af tvillingprimer) fra 1923. Papiret indeholder flere lignende formler, der alle er baseret på den samme metode, som de havde brugt til at løse mange problemer tidligere. Dette var deres cirkelmetode. Deres udledning af formlen for $\pi_{2}(x)$ er slet ikke stringent, men den er meget overbevisende. Der findes en kortfattet redegørelse for dette i et bilag til Andrew Granvilles artikel.
Men lige efter anden verdenskrig foreslog Lord Cherwell (Frederick Lindemann) en mere elementær probabilistisk (og stadig ikke stringent) udledning. Dette førte til et samarbejde med E. M. Wright og til sidst til en posthum fælles publikation. Dette er forklaret i afsnit 22.20 i Hardys og Wrights velkendte tekst. En lidt mere elementær version af dette kan også findes i et appendiks til Granvilles artikel (afsnit 2.5). Jeg følger ham.
Udgangspunktet for den plausible argumentation er vores estimat for $\pi(x)$, antallet af primtal mindre end eller lig med $x$. Den grundlæggende idé i afledningen er, at primtalene i et godt stykke hen ad vejen er tilfældigt fordelt. Vi ved, at tætheden af primtal i nærheden af $x$ er omkring $1/\log x$. Hvis primtalene var tilfældigt fordelt, ville sandsynligheden for, at to givne tal i nærheden af $x$ er primtal, blot være produktet af de lokale sandsynligheder, hvilket er $1/\log^{2} x$. Dette er helt sikkert en speciel argumentation, for hvis $n > 2$ er sandsynligheden for at både $n$ og $n+1$ er primtal $0$, mens det faktum, at $p$ er et primtal, synes at øge chancerne for at $p+2$ er et primtal. Der er lignende overvejelser at tage hensyn til på grund af eventuel delelighed med andre små primtal også i nærheden af $x$.
Der er et enkelt faktum i denne historie. Hvis $q$ er et vilkårligt primtal, så er sandsynligheden for at vælge et tilfældigt heltal, der ikke er deleligt med $q$, $1-1/q$. Sandsynligheden for at vælge to, der ikke er delelige med $q$, er derfor produktet $(1 – 1/q)^{2}$. Antag, at $p$ og $p+2$ begge er primtal, så er hverken $p$ eller $p+2$ deleligt med $q$. Hvis $q = 2$, sker dette 1/2$ gangen. Hvis $q \ne 2$, er sandsynligheden for, at $p \not\equiv 0$ og $p \not\equiv -2$ modulo $q$ er $(1 – 2/q)$. På grund af den kinesiske restsætning er delbarhed med to primtal en uafhængig begivenhed. Så hvis $x$ er stor, og $Q$ er relativt lille, er sandsynligheden for, at ethvert talpar $m$ og $n$ i nærheden af $x$ ikke er et multiplum af et primtal op til $Q$, $$ { 1\over 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} } \, . $$
Lad $\Gamma_{Q}$ være forholdet mellem dette og $\prod_{q \le Q}(1 – 2/q)$: $$ \Gamma_{Q}} = { 1\over 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} \over (1 – 2/q) } $$ Vi har $$ { 1 – 2/q \over (1-1/q)^{2} } = { (1 – 1/q)^{2} – 1/q^{2} \over (1 – 1/q)^{2} } = 1 – { 1 \over (q -1)^{2} } \, . $$ Et standardkriterium hævder, at dette produkt konvergerer, hvis summen $\sum 1/(q-1)^{2}$ konvergerer. Men det konvergerer faktisk, da integralprøven fortæller os, at $\sum 1/n^{2}$ konvergerer. Derfor konvergerer dette produkt faktisk til et tal $\Pi_{\infty}$ som $Q \rightarrow \infty$. Lad $C_{2}$ være dets inverse. I afsnit 2.5 i Granvilles artikel står der, at det på dette punkt burde være intuitivt fornuftigt, at antallet $\pi_{2}(x)$ af tvillingprimer $\le x$ tilnærmes ved $$ \$Pi_{2}(x) = C_{2} \int_{2}^{\infty} { dx \over \log^{2} x } \, . $$$
Teksten af Hardy og Wright udlægger en mere omhyggelig analyse, der gør det intuitive spring lidt klarere.
Værdien af konstanten her blev for lang tid siden beregnet af J. W. Wrench til at være omkring $1.320323236313169693739147855556242222002911155686525 \ldots $. Her er en sammenligning af nogle værdier af $\pi_{2}(x)$ og formlen i intervallet $$: $$ \matrix{ n & 10.000 & 20.000 & 30.000 & 40.000 & 50.000 \cr \pi_{2}(n) & 205\phantom{.0} & 342 \phantom{.0} & 467 \phantom{.0} & 591 \phantom{.0} & 705 \phantom{.0} & \cr \Pi_{2}(x) & 214,2 & 357,7 & 486,7 & 607,4 & 722,5 \cr } $$ $$ $$ \matrix{ n & 60.000 & 70.000 & 80.000 & 90.000 & 100.000 \cr \pi_{2}(n) & 811 \phantom{.0} & 905 \phantom{.0} & 1007 \phantom{.0} & 1116 \phantom{.0} & 1224\phantom{.0} \cr \Pi_{2}(x) & 833.3 & 940.9 & 1045.7 & 1148.2 & 1248.7 \cr } $$
Kommentarer?
Dicksons formodning
Dobbelt primtal er et specialtilfælde af noget langt mere generelt. Man kan spørge, om der er uendeligt mange par $p$, $p+4$ eller $p$, $p+6$, der er primtal? Eller $p$, $p+10$? Tilfældet med $p$ og $p+10$ er i hvert fald antydet af et af billederne ovenfor, hvor sådanne par er let synlige. Hvad med tripler af en eller anden art? Lad os antage, at $a_{1}$, $a_{2}$, $\ldots$ , $a_{k}$ udgør et array af hele tal. Kan vi forvente, at der findes et uendeligt antal sæt $n+a_{1}$, $n+a_{2}$, $\ldots$ , $n+a_{k}$, som alle er primtal?
Man skal være lidt forsigtig. Der findes ikke primtalpar af formen $p$, $p+1$ (tidligere $p = 2$), fordi et af disse to tal skal være deleligt med $2$. På samme måde findes der efter $p = 3$ ingen primtalstripler $p$, $p+2$, $p+4$, fordi et af disse skal være deleligt med $3$.
Dette sidste eksempel burde være oplysende. Tallet $p+4$ er deleligt med $3$, hvis og kun hvis $p+1$ er deleligt med $3$. Derfor deler $3$ et af tallene $p$, $p+2$, $p+4$, hvis og kun hvis det deler $p$, $p+1$, $p+2$. Men dette er sikkert, da den sidste tripel klart dækker alle tal modulo $3$.
Generelt siges $p$ at være en hindring for rækken $(a_{i})$, hvis $p$ altid deler mindst ét af hver sekvens $n+a_{i}$ ($i = 1$, $\ldots$, $k$). Dette sker, hvis og kun hvis tallene $a_{i} \; {\rm mod} \, p$ fylder hele $Z/p$.
Dette kan aldrig ske, hvis $p > k$, så for at kontrollere, om nogle $p$ hindrer $(a_{i})$, behøver vi kun at kontrollere, om $a_{i}$ dækker $Z/p$ for alle $p \le k$. Vi kalder arrayet $(a_{i})$ antageligt, hvis det ikke har nogen primtalobstruktioner.
For eksempel er $(1,3,7,9)$ et antageligt array, da, som man let kan kontrollere, hverken $2$ eller $3$ er en obstruktion. Flere primfølger, der passer ind i dette mønster, kan ses i et af diagrammerne ovenfor. Andre eksempler er (a) enhver $0$, $2n$; (b) $0$, $4$, $6$; (c) $0$, $2$, $6$.
Der findes vilkårligt store tilladelige mængder. Faktisk:
Theorem. Hvis $a_{1}$ til $a_{k}$ er en hvilken som helst mængde af forskellige primtal $> k$, udgør de en tilladelig mængde.
Hvorfor er dette? Hvis $p$ er et vilkårligt primtal, hvor $p> k$, så har vi allerede set, at det ikke kan være en obstruktion. Men hvis $p \le k$, så kan det ikke dele nogen af de $a_{i}$, hvoraf ingen kan være kongruent med $0$ modulo $p$. Så $a_{i}$ fylder ikke $Z/p$.
Et specialtilfælde af en formodning, der oprindeligt blev fremsat af L. E. Dickson, er, at hvis der ikke findes nogen primobstruktioner til $(a_{i})$, så findes der et uendeligt antal primfølger af formen $(n +a_{i})$.
Hvad der er sket for nylig
Dette er ikke stedet til at fortælle hele historien, som er blevet dækket grundigt andre steder. Jeg anbefaler især Quanta-artiklen af Erica Klarreich for en populær redegørelse og Granville’s essay for en mere teknisk redegørelse. Jeg vil blot gerne sige lidt mere præcist end i Klarreichs redegørelse, hvad det mest berømte af de nye resultater er.
Det skyldes Yitang Zhang. Den enkleste erklæring af det, han beviste, er, at der findes et uendeligt antal intervaller $[n, n+70.000.000.000)$, der indeholder mindst to primtal. Dette er svagere end twin primes conjecture, men begrebsmæssigt meget tæt på det. I efterfølgende arbejde (udført af mange matematikere) er størrelsen af intervallet blevet kraftigt reduceret, men der er formodentlig ingen måde at reducere det til $2$ med de nuværende metoder.
Som forklaret af Granville er Zhangs første og vel nok hans vigtigste resultat, at der findes $k$ med den egenskab, at hvis $a_{1}$, $\ldots$ , $a_{k}$ er et tilladeligt sæt af $k$ elementer, så findes der et uendeligt antal $n$ således, at $\{ n +a_{i} \}}$ indeholder mindst to primtal. (I Klarreichs Quanta-artikel kaldes rækken for en “kam”. Husk på, at i henhold til Dicksons formodning ville vi forvente at kunne sige, at alle $k$ er primtal). Faktisk har Zhang bevist, at denne påstand er sand for et bestemt $k =3.500.000$, der spænder over et interval på $70.000.000$. Den efterhånden berømte konsekvens er for nogle $m \lt 70.000.000$, at der findes et uendeligt antal primtalpar $p$, $p+m$.
Læs videre
- Lord Cherwell og E. M. Wright, “The frequency of prime patterns”, The Quarterly Journal of Mathematics 11 (1960).
De, der kender noget til Lord Cherwells liv, også kendt som Frederick Lindemann, vil blive meget overraskede over at høre om hans bidrag til talteorien. Wikipedias biografi antyder ikke i tilstrækkelig grad alle årsagerne til hans dårlige ry som Churchills vigtigste videnskabelige rådgiver under Anden Verdenskrig.
- L. E. Dickson, “A new extension of Dirichlet’s theorem on prime numbers”, Messenger of Mathematics 33.
Se også Wikipedia-indlægget om Dicksons formodning.
- Andrew Granville, “Primes in intervals of bounded length”. Kan fås fra hans hjemmeside.
- G. H. Hardy, Ramanujan, Cambridge University Press.
Afsnit 2.5 indeholder en ideel udledning af en mulig formel for $\pi(x)$.
- G. H. Hardy og J. E. Littlewood, “Some problems of ‘Partitio numerorum’ III: on the expression of a number as a sum of primes”, Acta Mathematica 44 (1923).
- G. H. Hardy and E. M. Wright, The theory of numbers, Oxford Press.
- Erica Klarreich, “Together and alone, closing the prime gap”, Quanta November 19, 2013.
- B. Riemann, “On the number of prime numbers less than a given quantity”. En engelsk oversættelse af denne klassiker af David Wilkins er tilgængelig via et link i Wikipedia.
Deri skitseres bl.a. en udledning af den omtrentlige formel for $\pi(x)$.
- J. W. Wrench, “Evaluation of Artin’s constant and the twin-prime constant”, Mathematics of Computation 76 (1961).
En tidlig beregning af $C_{2}$.
- Lister over primtal op til $1.000.000.000.000.000$
- En liste over de første 20.000 tvillingprimer.
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman