Halvadder og fuld adderkredsløb
Halvadder og fuld adderkredsløb er forklaret med deres sandhedstabeller i denne artikel. Design af Full Adder ved hjælp af Half Adder-kredsløb er også vist. Single-bit Full Adder-kredsløb og Multi-bit addition ved hjælp af Full Adder er også vist.
Hvor vi går ind i dette emne, er det meget vigtigt at vide noget om boolsk logik og logiske porte.
Kig på: BOOLEAN LOGIC
Kig på: LOGIC GATES
Kig på: FLIP FLOPS
Hvad er en adder?
En adder er en slags regnemaskine, der bruges til at addere to binære tal. Når jeg siger lommeregner, mener jeg ikke en med knapper, denne er et kredsløb, som kan integreres med mange andre kredsløb til en lang række anvendelser. Der findes to slags addere;
- Halvadder
- Fuldadder
Halvadder
Med hjælp af halvadder kan vi designe kredsløb, der er i stand til at udføre simpel addition ved hjælp af logiske gates.
Lad os først se på addition af enkeltbits.
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
Dette er de mindst mulige kombinationer af enkeltbits. Men resultatet for 1+1 er 10. Selv om dette problem kan løses ved hjælp af en EXOR-port, skal sumresultatet omskrives som et 2-bit output, hvis man er interesseret i outputtet.
Så kan ovenstående ligninger skrives som
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
Her bliver udgangen ‘1’af ’10’ til carry-out. Resultatet er vist i en sandhedstabel nedenfor. “SUM” er det normale output, og “CARRY” er carry-out.
INPUTS OUTPUTS
A B SUM CARRY
0 0 0 0 0
0 1 1 1 0
1 0 1 0 0
1 1 0 1 1
Fra ligningen, er det klart, at denne 1-bit adderer let kan implementeres ved hjælp af en EXOR-port for output “SUM” og en AND-port for overførslen. Tag et kig på implementeringen nedenfor.
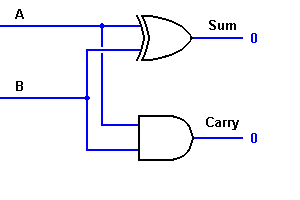
For kompleks addition kan der være tilfælde, hvor man skal lægge to 8-bit bytes sammen. Dette kan kun gøres ved hjælp af full-adder-logik.
Full Adder
Denne type adder er lidt vanskeligere at implementere end en halv adder. Den væsentligste forskel mellem en halv-adder og en fuldadder er, at fuldadderen har tre indgange og to udgange. De to første indgange er A og B, og den tredje indgang er et input carry, der betegnes som CIN. Når en fuld adderlogik er konstrueret, vil vi kunne sætte otte af dem sammen for at skabe en adder, der dækker en byte, og kaskadeoverføre carry-bitten fra den ene adder til den næste.
Udgangens carry betegnes COUT og den normale udgang betegnes S. Tag et kig på sandhedstabellen.
INDGANGE UDGANGE
A B CIN COUT S
0 0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 0 0 1
0 1 1 1 1 0
1 0 0 0 0 0 1
1 0 1 1 1 0
1 1 0 1 0 0
1 1 1 1 1 1 1
Fra ovenstående sandhed-tabel, kan den fulde adderlogik implementeres. Vi kan se, at udgangen S er en EXOR mellem indgangen A og den halve adder SUM-udgang med indgangene B og CIN. Vi skal også bemærke, at COUT kun vil være sandt, hvis en af de to indgange ud af de tre er HIGH.
Dermed kan vi implementere et fuldt adderkredsløb ved hjælp af to halve adderkredsløb. Den første halvadderkreds vil blive brugt til at addere A og B for at producere en delvis sum. Den anden halvadderlogik kan bruges til at tilføje CIN til den sum, der er produceret af den første halvadder, for at få den endelige S-udgang. Hvis en af halvadderlogikken producerer et carry, vil der være et output carry. COUT vil således være en OR-funktion af halvadderens Carry-udgange. Tag et kig på implementeringen af det fulde adderkredsløb, der er vist nedenfor.
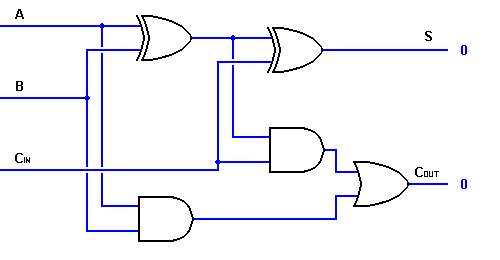
Og selv om implementeringen af større logiske diagrammer er mulig med ovenstående fulde adderlogik, bruges der for det meste et enklere symbol til at repræsentere operationen. Nedenfor gives en enklere skematisk repræsentation af en en-bits fuldadder.
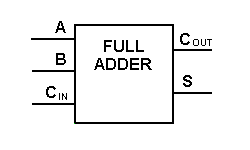
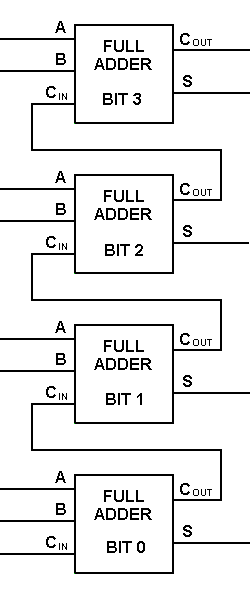
Med denne type symbol kan vi addere to bits sammen, idet vi tager en carry fra den næste lavere størrelsesorden og sender en carry til den næste højere størrelsesorden. I en computer skal hver bit for en multibitoperation repræsenteres af en fuld adderer og skal adderes samtidigt. For at addere to 8-bit tal skal man således bruge 8 fulde addere, som kan dannes ved at kaskadere to af 4-bit blokkene. Additionen af to 4-bit tal er vist nedenfor.