Alice, der går i fjerde klasse, spørger: “Hvor mange diagonaler er der i en decagon?”
Godt spørgsmål, Alice. Men i stedet for at give dig et svar på det spørgsmål, vil jeg vise dig, hvordan du selv kan finde ud af det. Og ikke nok med det, jeg vil vise dig, hvordan du kan finde ud af svaret for enhver polygon, selv om den har 20, 50 eller 2000 sider!
Er du klar? Lad os starte med et enkelt eksempel. Vi tager en polygon med 8 sider (som kaldes en ottekant), som her:
Nu har denne polygon, fordi den har otte sider, også otte hjørner. Det virker lidt overvældende at forsøge at finde ud af alle diagonalerne, så lad os bare fokusere på ét toppunkt. Hvor mange diagonaler kan man tegne i en ottekant, der alle begynder ved ét toppunkt?
Svaret på det spørgsmål er fem. Tag et kig på nedenstående diagram:

I dette diagram har jeg valgt diagonalen til venstre lige under det øverste toppunkt, og jeg har tegnet diagonaler til alle toppunkter, som jeg kan tegne en diagonal til. Hvilke diagonaler kan jeg ikke tegne diagonaler til? Jeg kan ikke tegne en diagonal fra et toppunkt tilbage til sig selv, og jeg kan ikke tegne diagonaler til de to toppunkter ved siden af dette toppunkt (for det ville ikke være diagonaler, det ville være sider!).
Der er altså tre toppunkter, jeg ikke kan tegne diagonaler til fra dette toppunkt. Otte hjørner i alt, minus de tre, jeg ikke kan tegne til, er der fem tilbage. Det er vigtigt at huske: Træk 3 fra antallet af hjørner, og du har antallet af diagonaler, som du kan tegne fra ethvert hjørne.
Men det er kun ét hjørne! Du kan tegne diagonaler fra ethvert toppunkt, ikke sandt? Ja, selvfølgelig! Og der er otte hjørner i vores ottekant, så vi tager antallet af diagonaler pr. hjørne og multiplicerer det med antallet af hjørner: 5 x 8 = 40.
Du kunne være fristet til at tro, at det er vores svar, men det er det ikke. Hvorfor ikke? Fordi vi har talt hver diagonal to gange! Hver diagonal har to hjørner, så vi har talt den fra den ene ende, og vi har også talt den fra den anden ende. Så for at få det faktiske antal diagonaler skal vi dividere vores svar med 2. 40 / 2 = 20. Der er tyve diagonaler i en ottekant.
Lad os prøve dette ræsonnement på en polygon, der har 2000 sider. Nu vil jeg ikke tegne en 2000-egon for jer; vi bliver bare nødt til at regne ræsonnementet ud uden et billede.
- Vælg et toppunkt. Hvor mange diagonaler kan du tegne fra dette toppunkt? Svar: 2000 – 3 = 1997.
- Hvor mange hjørner i alt? Svar: 2000
- Hvor mange diagonaler regnet fra alle hjørnerne? Svar: Hvor mange diagonaler er der talt fra? 1997 x 2000 = 3.994.000
- Ops! Vi har talt hver diagonal to gange! Hvordan slipper vi af med de dobbelte? Svar: 3994000 / 2 = 1.997.000
Så en 2000-gon har 1.997.000 diagonaler!
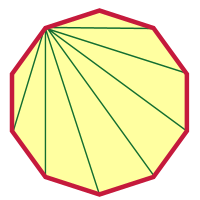
Efter at have lavet noget så vanvittigt som en 2000-gon, burde en decagon ikke virke så svært, vel? Jeg får dig i gang, og du kan afslutte det herfra. Jeg valgte et toppunkt og tegnede diagonaler fra dette toppunkt.
Hvor mange er der? Kunne du regne ud, hvor mange der var, uden at se på billedet?
Kan du regne det ud herfra? Det håber jeg da! Held og lykke, Alice.
Forresten er der en formel, du kan bruge; den ser sådan her ud: D = n(n – 3)/2. Men ærligt talt forventer jeg ikke, at mine elever skal lære den udenad. Jeg forventer, at de kan huske, hvordan vi ræsonnerer det her. Hvis man forstår logikken, er det endnu bedre end at have en formel!