Standardformlen til at finde determinanten af en 3×3 matrix er en opdeling af mindre 2×2 determinantproblemer, som er meget nemme at håndtere. Hvis du har brug for en genopfriskning, kan du tjekke min anden lektion om, hvordan man finder determinanten af en 2×2-matrix. Lad os antage, at vi får en kvadratisk matrix A, hvor,
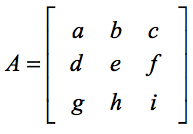
Determinanten af matrix A beregnes som
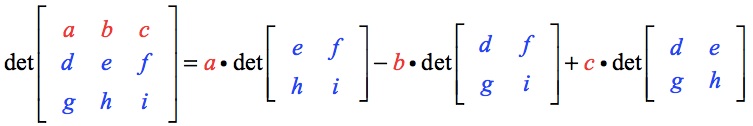
Her er de vigtigste punkter:
- Bemærk, at de øverste rækkeelementer nemlig a, b og c tjener som skalarmultiplikatorer til en tilsvarende 2×2-matrix.
- Skalaren a multipliceres med den 2×2-matrix af overskydende elementer, der opstår, når der trækkes lodrette og vandrette linjestykker, der går gennem a.
- Det samme sker for at konstruere 2×2-matricerne for de skalare multiplikatorer b og c.
Determinant af 3×3-matrix (animeret)

Eksempler på, hvordan man finder determinanten af en 3×3-matrix
Eksempel 1: Find determinanten af nedenstående 3×3-matrix.
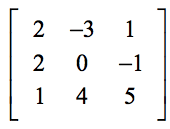
Den nedenstående opstilling vil hjælpe dig med at finde korrespondancen mellem de generiske elementer i formlen og elementerne i den aktuelle opgave.
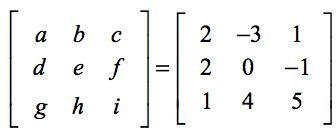
Ved anvendelse af formlen,


Eksempel 2: Vurder determinanten af nedenstående 3×3-matrix.
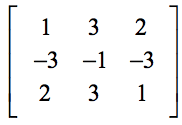
Vær meget omhyggelig med at indsætte værdierne de rigtige steder i formlen. Almindelige fejl opstår, når eleverne bliver uforsigtige i det første trin med substitution af værdierne.
Dertil kommer, at du skal tage dig god tid til at sikre dig, at din aritmetik også er korrekt. Ellers vil en enkelt fejl et sted i beregningen give et forkert svar i sidste ende.
Da,
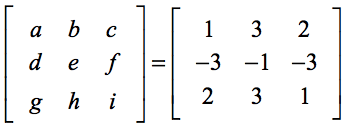
vores beregning af determinanten bliver…

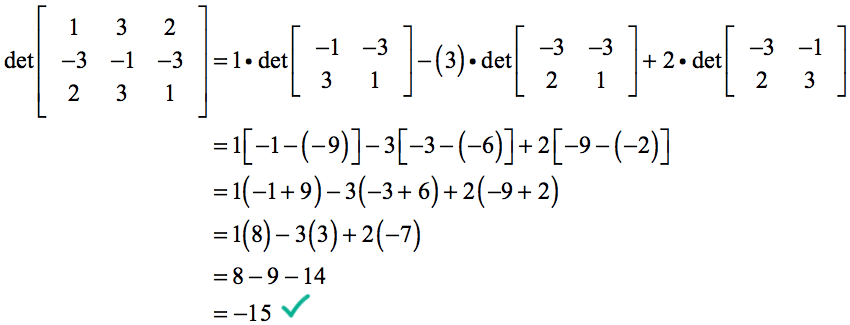
Eksempel 3: Løs determinanten for nedenstående 3×3-matrix.
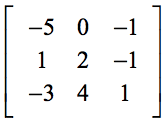
Nærværet af nul (0) i den første række skulle gøre vores beregning meget lettere. Husk, at disse elementer i den første række, fungerer som skalare multiplikatorer. Derfor vil nul ganget med noget resultere i, at hele udtrykket forsvinder.