Du er en desperat universitetsstuderende, der forsøger at skrive din sidste opgave, inden du tager din eksamen. Alt du ønsker at gøre er at blive færdig og fejre din præstation. Pludselig kommer der en person ind i den bås, du har arbejdet i hele dagen. Denne person ligner dig meget, men du har ikke tid til at regne ud, hvad der foregår, for hun giver dig straks et USB-drev og siger, at du skal aflevere den opgave, der er på drevet. “Så kan du gå ud og fejre det,” siger hun smilende, mens hun hurtigt forlader stedet og går ind i den nærliggende trappeopgang. Du rejser dig op og går efter hende, men hun synes at være forsvundet.
Du går tilbage til dit kontor, åbner opgavens fil, læser den hurtigt igennem og afleverer opgaven efter at have kvast dit etiske dilemma. Et par dage senere modtager du din karakter: et A+. Du går på jagt efter den mystiske fremmede, der gav dig denne vidunderlige opgave, og du ender tilbage i trappeopgangen. Du går ind og tænker på, hvor den fremmede kunne være gået hen. Efter et øjeblik eller to forlader du stedet. Da du går forbi den bås, du havde knoklet så længe i, ser du dig selv! Så går det op for dig. Du må give dig selv papiret. Heldigvis havde du lagt USB-drevet i din lomme, og da du er en usædvanlig usoigneret universitetsstuderende, har du stadig de samme bukser på. Du går ind i kabinen, giver dig selv USB-drevet, giver dig selv nogle instruktioner og flygter straks tilbage til trappeopgangen, som transporterer dig tilbage til din nutid.
Hvordan kan du give dig selv en opgave, som ingen har skrevet? Hvordan kan det, at du afleverer papiret, få dig til at aflevere papiret?
Hvad er kausale sløjfer?
En kausal sløjfe er en sekvens af begivenheder e1, … , en. Hver begivenhed i løkken er en af årsagerne til den næste begivenhed. Den sidste begivenhed en er en af årsagerne til den første begivenhed e1. Hvis en årsagssløjfe ikke har nogen eksterne (uden for sløjfen) årsager eller virkninger, er denne årsagssløjfe en lukket årsagssløjfe; ellers er den en åben årsagssløjfe. Tænk på lukkede årsagssløjfer som kausalt isolerede. Tænk på åbne årsagssløjfer som kausalt indlejrede.
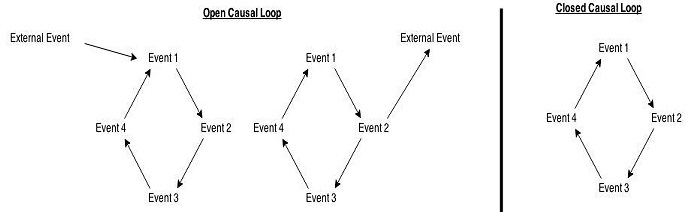
Figur 1: To slags årsagssløjfer
Er årsagssløjfer umulige?
Tanken om årsagssløjfer opfattes nogle gange som værende vært for et iboende paradoks. Årsagerne til denne bekymring varierer.
Ræsonnement 1: Der skal være en uforårsaget første årsag til enhver begivenhed. Loops kan opstå ex nihilo (fra ingenting) tilsyneladende uden en ultimativ første årsag. Denne bekymring kan løses ved at sammenligne årsagssløjfer med mere almindelige årsagskæder. En årsagskæde er en sekvens af begivenheder, hvor hver begivenhed forårsager den næste begivenhed i sekvensen (en årsagssløjfe er en særlig form for årsagskæde). Nogle årsagskæder er ikke sløjfer; de består af begivenheder i en sekvens, hvor hver begivenhed tidsmæssigt følges af og forårsager den næste begivenhed i sekvensen. Der er intet i denne definition, der kræver, at kæden skal have en begyndelse (eller en slutning). Derfor virker det lidt mærkeligt at insistere på, at begivenheder i et kausalt loop kræver en ultimativ første årsag. Den eneste forskel mellem årsagskæder og årsagssløjfer er, at når man følger årsagssammenhængen langs en årsagssløjfe, ender man til sidst tilbage, hvor man startede.
Dertil kommer, at årsagssløjfer har, og synes endda at være forpligtet til at have en første årsag. Enhver årsagssløjfe vil have mindst én begivenhed, der indtræffer tidligere end alle de andre. Denne begivenhed viser sig ikke altid at være en eller anden ultimativ første årsag, der forklarer hele løkken. Men eftersom den første begivenhed indtræffer før de andre begivenheder i tidslinjen, er den alligevel den første. Det er den tidligste begivenhed i loopet.
Ræsonnement 2: Truslen om cirkulære forklaringer. Overvej tidligere end, et forhold, der ofte forbindes med en begivenhed, der forårsager en anden begivenhed. Traditionelt antages denne relation at være transitiv; det vil sige, at hvis begivenhed a er tidligere end begivenhed b, og begivenhed b er tidligere end begivenhed c, så er begivenhed a tidligere end begivenhed c. Men hvis man antager, at årsagssammenhængen er transitiv, og man anvender den vedrørende en årsagssløjfe, bryder tingene sammen. Hvis kausaliteten er transitiv, er enhver begivenhed i et kausalt loop en årsag til sig selv. I en årsagssløjfe med tre hændelser fungerer kausaliteten godt til at sige, at begivenhed a forårsager b og b forårsager c og c forårsager a, men medmindre kausaliteten ikke er transitiv, fører disse tre kendsgerninger til den konklusion, at a forårsagede a. At a forårsagede a er bestemt ikke en informativ forklaring på a. Heldigvis behøver vi, selv om kausaliteten er transitiv, ikke at antage, at de tilsvarende forklarende sammenhænge er bevaret. Ulrich Meyer (2012, 261) mener, at en kombination af alle de lokale forklaringer fører til en svagere forklaring.
Ræsonnement 3: Enhver sekvens af begivenheder skal have en tilstrækkelig forklaring på, hvorfor sekvensen opstår på den måde, den gør. Hvis enhver hændelsessekvens skal have en tilstrækkelig forklaring, belyses det potentielle problem ved at overveje jinn. En jinni er et objekt, der er en del af begivenhederne i løkken, og som ser ud til at komme til verden fra ingenting. Et glimrende eksempel på en jinni er Swanns halskæde fra Timerider: The Adventure of Lyle Swann.
I denne film fra 1982 bliver Swann ved et uheld sendt tilbage i tiden og møder en kvinde ved navn Claire, som til sidst forfører ham. Efter en række spektakulære begivenheder redder de mennesker, der ved et uheld transporterede ham tilbage i tiden, Swann. Lige før han bliver reddet, snupper Claire halskæden, der blev overdraget til Swann fra hans tipoldefars oldemor, som stjal den fra hans tipoldefars oldefar. Halskæden er en jinni, fordi Swann får halskæden af sin tip-oldefarmor, som stjal den samme halskæde fra ham år tidligere. Som du måske har gættet, er Claire Swanns tip-oldebedstemor. Swann selv er sin egen tipoldefar.
Problemet, som halskæden og de fleste jinn udgør, er kilden til deres eksistens. Hvordan kan en fysisk genstand som en halskæde bare eksistere? Hvem har designet halskæden? Hvad forklarer, hvorfor det er en halskæde i stedet for f.eks. et armbånd? Der må være en eller anden forklaring på, hvorfor halskæden er, som den er. Ikke sandt?
Der er forklaringer på de forskellige stadier af halskædens eksistens. Halskæden har årsager. At Swann modtager halskæden fra sin bedstemor er en årsag til, at han tager den med sig tilbage i tiden. At halskæden går tilbage i tiden er en årsag til, at Claire er i stand til at stjæle halskæden osv. Derudover kan man argumentere for, at universet og naturlovene må have en bestemt struktur, for at der kan eksistere kausale sløjfer. Disse love ville også være en kilde til brugbare forklaringer.

Figur 2: Timerider Timeline
Nogle kendsgerninger synes dog at være dømt til at forblive uforklarlige, kendsgerninger som f.eks. at halskæden er en halskæde og ikke et armbånd. Desuden, hvorfor er der en årsagssløjfe i stedet for ingen årsagssløjfe? Viser vores manglende evne til at forklare disse kendsgerninger, at der er noget usammenhængende ved kausalsløjfer? Nej; problemet med dette ræsonnement er, at der opstår lignende problemer med hensyn til normale objekter. Man kan se årsagerne til en stol, fordi man kan se snedkeren bygge stolen af træ, men hvad har skabt træet? Og endnu mere, hvad har skabt de atomer, som træet består af? Man kan blive ved med at stille disse spørgsmål, men en fuldstændig og fyldestgørende forklaring er måske næsten umulig at komme videre med under normale omstændigheder. Der er mange kendsgerninger og genstande, som vi måske aldrig finder en god forklaring på.
For at gå et skridt videre med denne analyse kan man overveje oprindelsen af halskædens kunstneriske design. Halskæden så ud til at være en normal halskæde, en halskæde, der var blevet udformet med hensigt og kunstfærdighed. Dette rejser spørgsmålet om, hvor kunstnerisk kunstfærdighed kom fra. Hvem (eller hvad) har brugt sine færdigheder og sin viden på at skabe denne halskæde? Storrs McCall (2010) siger, at der ikke findes nogen løsning på dette problem. Måske har nogle fakta simpelthen ikke nogen forklaringer. At insistere på, at alting skal have en forklaring, er uberettiget.
Kræver tidsrejser kausalsløjfer?
Den påstand, at alle tidsrejser må omfatte mindst én kausalsløjfe, er meget udbredt. I sit essay fra 2009 om dette emne præsenterer Bradley Monton denne holdning ved hjælp af et citat af D.H. Mellor. Ifølge Monton argumenterer Mellor mod muligheden for tidsrejser ved at “‘udelukke de årsagssløjfer … som cyklisk tid og tidsrejser baglæns har brug for'” (Monton, 2009, 55; Mellor 1998, 131) (Monton, 2009, 55; Mellor 1998, 131). Ifølge Mellor og andre vil en tidsrejsende, når han rejser tilbage i tiden, altid have handlinger i fortiden, som påvirker tidsrejsendes rejse tilbage i tiden.
Her er et enkelt eksempel på dette fænomen: I 2020 bygger Jim en tidsmaskine ud fra nogle tegninger, han fandt på sit loft, og beslutter sig for at rejse tilbage for at se sit yngre jeg. Så Jim rejser tilbage til 1990 og finder sit yngre jeg. Jim giver sit yngre jeg planerne til tidsmaskinen til sit yngre jeg. Hans yngre jeg finder tanken om tidsrejser absurd og gemmer derfor tegningerne på sit loft. I 2020 finder Jim så disse planer og bygger sin tidsmaskine.
Det er klart, at Jim kun kan tage på sit tidsrejseeventyr, hvis Jim overhovedet tager på eventyret. Jims handlinger eller blot hans tilstedeværelse ved ankomsten kan på en eller anden måde have påvirket hans yngre jeg på en måde, der fører til hans rejse tilbage i tiden. Mere præcist ser det ud til, at enhver rejse til fortiden på en eller anden måde ville interagere med mennesker, genstande eller partikler, som i sidste ende vil bevæge sig fra fortiden til fremtiden, hvilket betyder, at alle tidsrejser resulterer i et kausalt loop. Potentialet for en ændring, der på en eller anden måde forårsager en kæde af begivenheder, som påvirker den rejse til fortiden, der producerede den oprindelige ændring, synes at være ægte.
Det at have potentialet til at forårsage en begivenhed kræver imidlertid ikke, at begivenheden indtræffer. Monton hævder at have fundet frem til en hypotetisk situation, der involverer tidsrejser uden kausale sløjfer. Han beskriver et univers, der er opdelt i to regioner, som kun indeholder A-, B- og C-partikler. (Se figur 1.) Region 1 indeholder kun A- og C-partikler og området op til grænsen mellem de to regioner. Region 2 indeholder kun B- og C-partikler og området op til og med den samme grænse. Et kraftfelt forhindrer B-partikler i at krydse grænsen til region 1. C-partiklerne interagerer aldrig med hverken A- eller B-partikler og bevæger sig frit mellem region 1 og 2. Når en A-partikel krydser grænsen, bliver partiklen straks forvandlet til en B-partikel.
Tænk nu på følgende scenarie: En A-partikel bevæger sig mod grænsen. I samme øjeblik, som partiklen når grænsen, bliver den omdannet til en B-partikel og begynder også at rejse tilbage i tiden. Mens A-partiklen rejser i tiden, følger den grænsen, hvilket forhindrer A-partiklen i at interagere med nogen af de andre partikler. På baggrund af de indledende betingelser i dette eksempel er denne A-partikel den eneste, der kan nå grænsen. Så snart partiklen ophører med at tidsrejse, bevæger A-partiklen sig ind i region 2 (Monton 2009, 60).
Figur 3: Montons eksempel
Det ser ud til, at A-partiklen er i stand til at tidsrejse uden at interagere med nogen af partiklerne i begge regioner, herunder sit yngre jeg. Mens den tidsrejser til fortiden, og efter at den er stoppet med at tidsrejse, forhindrer grænsen denne partikel i at interagere med sin afgang til fortiden. Det betyder, at partikel A med succes har tidsrejst uden at indgå i en kausal løkke, da A-partiklens tidsrejse ikke kunne have forårsaget, at netop denne partikel havde indledt sin tidsrejse.
I almindelighed, især i mere realistiske situationer, i situationer med en fysik, der mere ligner vores egen, virker det usandsynligt, at begrebet tidsrejse til fortiden uden at kausale løkker opstår i en eller anden form. Der er behov for en yderst omhyggelig og specifik beskrivelse for at generere Montons smarte scenarie.
Kræver kausalsløjfer tidsrejser?
En kausal løkke vil altid indeholde bagudrettet årsagssammenhæng, simpelthen fordi en af begivenhederne i løkken på et eller andet tidspunkt må være årsag til en tidligere begivenhed. Dette beviser dog ikke, at alle årsagssløjfer vil indeholde tidsrejser. Indeholder bagudrettet årsagssammenhæng altid tidsrejser?
I nogle tilfælde nej, og i andre tilfælde ja. I et univers, hvor objekter kun kan påvirke et objekt, der eksisterer på samme tid som det selv, ville tidsrejser være nødvendige for at påvirke objekter på et tidligere tidspunkt. For at et objekt kan påvirke objekter i en anden tid end objektets egen tid, ville dette objekt være nødt til at rejse til den anden tid og på det tidspunkt påvirke det andet objekt. Hvis universet imidlertid tillod objekter at påvirke hinanden fra forskellige tidspunkter i tiden, ville tidsrejser ikke længere være nødvendige. Da baglæns årsagssammenhæng ikke kræver tidsrejser, er kausalsløjfer i forlængelse heraf heller ikke nødvendige.
Kausalsløjfer og flerdimensional tid
Tidsstrukturen med forgreninger af tidslinjer – undertiden kaldet flerdimensional tid – fjerner de fleste af de interessante træk ved kausalsløjfer. (Se emnesiden om flerdimensional tid på vores websted.) Faktisk indføres den nogle gange for at holde årsagssløjfer ude (Deutsch 1991, Deutsch og Lockwood 1994). Med flerdimensional tid medfører tidsrejser, at tidslinjerne deles op, så en begivenhed ikke kan forårsage en begivenhed langs sin egen fortidige gren. Dette “pakker” løkkerne ud, og det eneste, der er tilbage, er en række opdelte årsagskæder. En konsekvens af dette er, at hvis flerdimensional tid var sandt, ville svaret på spørgsmålet om, hvorvidt tidsrejser til fortiden altid indebærer en årsagssløjfe, være et rungende nej. En tidsrejsende skaber grene i stedet for sløjfer.
Kausalsløjfer og fysik
For at introducere nogle teoretiske kausalsløjfer i forbindelse med fysik, lad os overveje ideen om en tidslignende kurve. En tidslignende kurve er et objekts vej gennem rumtiden, hvor objektet fortsætter lokalt fremad i tiden med tidslignende forbindelser mellem hvert interval. Et kausalt loop opstår, når et objekts tidslignende kurve looper tilbage på sig selv.
En måde at introducere et kausalt loop på er med ideen om, at universet har en sammenrullet rumtid (Gott 2001, 82-85). Den bedste analogi for denne idé er en cylinder, hvor de dimensioner, der udgør rummet, er cylinderens akser. Denne struktur gør det muligt for et objekts tidslignende kurve at lave en sløjfe rundt om cylinderen og mødes med sig selv.
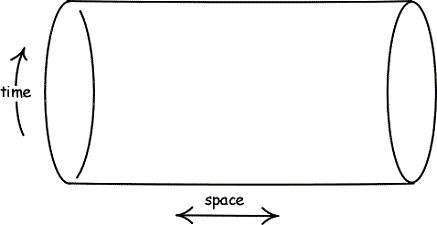
Figur 4: Krøllet rum-tid
Vormhulsbaserede tidsrejser giver også mulighed for lukkede tidslignende kurver, se temasiden Relativitetsteori og tidsrejser på vores hjemmeside.
Fysikken stiller nogle alvorlige problemer for muligheden for jinn. I henhold til termodynamikkens anden lov stiger entropien (eller uorden) altid med tiden. Tænk på eksemplet med halskæden i Timerider. Ifølge termodynamikken ville halskædens entropi under normale omstændigheder stige fra det øjeblik Claire stjæler halskæden, til halskæden bliver givet videre til Swann, og indtil Swann rejser tilbage i tiden. Nu ændrer de fleste opfattelser af tidsrejser ikke objekters tilstand, når de rejser tilbage i tiden. Men da halskædens entropi lige før Swann rejser tilbage skulle have den samme entropi, som da Swann ankommer til fortiden, ville dette give en modsigelse. Der opstår en modsigelse, fordi halskædens entropi lige før Swann tager af sted både er lig med og større end entropien, når Swann ankommer i fortiden. Denne modsigelse betyder, at for at jinn kan eksistere, må tidsrejse-modeller på en eller anden måde gøre rede for at reducere entropien for dens tilbagevenden til fortiden (Gott 2001, 23).
En sidste interessant anvendelse af kausale sløjfer i fysikken er hypotesen om, at universet snarere end at stamme fra et big bang, begyndte som en rum-tid ‘doughnut’, hvorfra resten af universet forgrenede sig. Forfatterne til denne teori, J. Richard Gott og Li-Xin Li (Gott 2001, 186-199), formulerede denne teori på grundlag af en alternativ løsning på Einsteins feltligninger. Rum-tids-doughnutten er i det væsentlige en kausal løkke med både lukkede og åbne stier rundt om løkken. Så nogle stier gennem rumtiden eksisterer som en løkke, men der er andre, der forgrener sig til resten af universet og dets indhold (jf., Meyer 2012, 259).
Konklusion
Lad os vende tilbage til det indledende eksempel om den moralsk tvetydige terminsprøve og se nærmere på det. Som du måske har gættet ud fra resten af denne diskussion, kan vi ganske vist analysere nogle aspekter af denne historie med succes, men mange interessante spørgsmål er stadig åbne for diskussion. Har du f.eks. dermed plagieret, da du afleverede opgaven? Du har aldrig sat dig ned og skrevet opgaven, men du har heller ikke kopieret eller endog støttet dig på nogens arbejde! Et andet eksempel: Er idéerne i papiret jinn? Er de digitale oplysninger på USB-drevet en jinni? Er selve USB-drevet en jinni? Er historien i overensstemmelse med termodynamikken? Intet i historien antyder, at entropien på en eller anden måde ikke stiger, mens USB-drevet lå i dine bukser i en uge. På trods af disse åbne spørgsmål er vi ikke stødt på noget iboende paradoks i forbindelse med kausale sløjfer.
Referencer og yderligere læsning
Arntzenius, Frank og Maudlin, Tim. “Tidsrejser og moderne fysik”. The Stanford Encyclopedia of Philosophy (Winter 2013 Edition), Edward N. Zalta (red.), <http://plato.stanford.edu/archives/win2013/entries/time-travel-phys/>.
Dear, William. (instruktør). Timerider: The Adventures of Lynn Swann . USA: Zoomo Productions, 1982.
Deutsch, David. ‘Quantum Mechanics Near Closed Timelike Lines’. Physical Review D 44 (1991): 3197-3217.
Deutsch, David, og Lockwood, Michael. ‘The Quantum Physics of Time Travel’. Scientific American 270 (1990): 68-74.
Gott, J. Richard. Tidsrejser i Einsteins univers. Boston: Houghton-Mifflin, 2001.
McCall, Storrs. “Et uløseligt problem”. Analysis 70 (2010): 647-648.
Mellor, D. H. Real Time. London: Routledge, 1998.
Meyer, Ulrich. “Explaining Causal Loops.” Analysis 72 (2012): 259-264.
Monton, Bradley. “Time Travel without Causal Loops”. The Philosophical Quarterly 59 (2009): 54-67.
For side credits, se siden “Topics-Page Credits”.