Det er ikke ofte, at en matematisk ligning kommer i den nationale presse, langt mindre i den populære radio, eller, hvad der er mest forbløffende af alt, er genstand for en debat i det britiske parlament. Men i 2003 var den gode gamle kvadratiske ligning, som vi alle lærte om i skolen, alle disse ting.
Hvor vi begynder

Det hele startede på et møde i National Union of Teachers. Den kvadratiske ligning blev holdt højt til nationen som et eksempel på den grusomme tortur, som matematikere påførte stakkels intetanende skolebørn. Den kvadratiske ligning, der var fascineret af denne beskyldning, accepterede en hovedrolle i radioen på bedste sendetid, hvor den blev udspurgt af en formidabel interviewer, der var mere vant til at tage kampen op med premierministeren. The (London) Times brugte plads i sin lederspalte, som normalt er forbeholdt tunge diskussioner om den moderne verdens moralske (eller anden) sundhed, til at proklamere, at den kvadratiske ligning var ubrugelig, at matematik var ubrugelig, og at ingen ønskede at studere matematik alligevel, så hvorfor bekymre sig om det. Da man var bekymret for, at den kvadratiske lignings farlige indrømmelser ikke skulle forblive uanfægtede, blev ligningens afgørende betydning for Det Forenede Kongeriges overlevelse debatteret i det britiske underhus (der blev indtaget en positiv holdning, hvilket De måske er glad for at høre).
Hvor ville det hele ende? Var den kvadratiske ligning virkelig død? Var der nogen, der var ligeglade? Er matematikere virkelig onde monstre, der kun ønsker at påføre en yngre generation kvadratiske ligninger som et middel til at fordærve deres udødelige sjæle?
Måske det, men det er egentlig ikke den kvadratiske lignings skyld. Faktisk har den kvadratiske ligning spillet en central rolle ikke blot for hele den menneskelige civilisation, som vi kender den, men også for den mulige opdagelse af andre fremmede civilisationer og endda for så vitale moderne aktiviteter som at se satellit-tv. Hvad andet, bortset fra den guddommelige åbenbarings natur, kan anses for at have haft en sådan indflydelse på livet, som vi kender det? Faktisk kan kvadratiske ligninger i en meget reel forstand redde dit liv.
Babylonierne
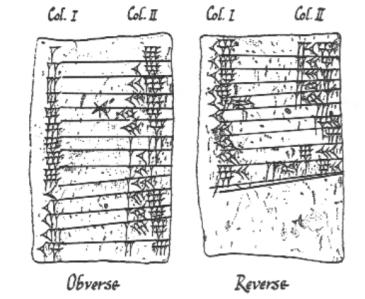
Babyloniske kileskrifttavler, der optegner de 9 gangetabeller
Det hele startede omkring 3000 f.Kr. med babylonierne. De var en af verdens første civilisationer og kom med nogle fantastiske ideer som landbrug, kunstvanding og skrivning. De tegnede solens, månens og planeternes baner og nedskrev dem på lertavler (som du stadig kan se på British Museum). Det er babylonierne, vi skylder de moderne idéer om vinkler, herunder den måde, hvorpå cirklen er delt op i 360 grader (på grund af en lille regnefejl, én pr. dag). Vi skylder også babylonierne den noget mindre behagelige opfindelse af det (frygtede) skattevæsen. Og dette var en af grundene til, at babylonierne havde brug for at løse kvadratiske ligninger.
Lad os antage, at du er en babylonisk landmand. Et eller andet sted på din gård har du en firkantet mark, hvor du dyrker en eller anden afgrøde. Hvor meget af din afgrøde kan du dyrke på marken? Hvis du fordobler længden af hver side af marken, finder du ud af, at du kan dyrke fire gange så meget af afgrøden som før. Grunden til dette er, at den mængde afgrøde, du kan dyrke, er proportional med arealet af marken, som igen er proportional med kvadratet på længden af siden. Hvis  er længden af siden af marken, er
er længden af siden af marken, er 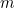 matematisk set den mængde afgrøde, man kan dyrke på en kvadratisk mark med sidelængde 1, og
matematisk set den mængde afgrøde, man kan dyrke på en kvadratisk mark med sidelængde 1, og  er den mængde afgrøde, man kan dyrke, så
er den mængde afgrøde, man kan dyrke, så
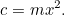 |
Dette er vores første kvadratiske ligning, nøgen og blinkende i sollyset. Kvadratiske ligninger og arealer er knyttet sammen som brødre og søstre i samme familie. Lige nu behøver vi dog ikke at løse noget – indtil skattemanden kommer, vel at mærke! Han siger muntert til landmanden: “Jeg vil gerne have, at du giver mig afgrøder til at betale for skatterne på din gård.” Landmanden står nu over for et dilemma: Hvor stor en mark skal han bruge for at dyrke den mængde afgrøder? Vi kan nemt besvare dette spørgsmål, faktisk
afgrøder til at betale for skatterne på din gård.” Landmanden står nu over for et dilemma: Hvor stor en mark skal han bruge for at dyrke den mængde afgrøder? Vi kan nemt besvare dette spørgsmål, faktisk
 |
Det er nemt for os at finde kvadratrødder ved hjælp af en lommeregner, men det var mere et problem for babylonerne. Faktisk udviklede de en metode til successiv tilnærmelse af svaret, som er identisk med den algoritme (kaldet Newton-Raphson-metoden), som moderne computere bruger til at løse meget sværere problemer end kvadratiske ligninger.
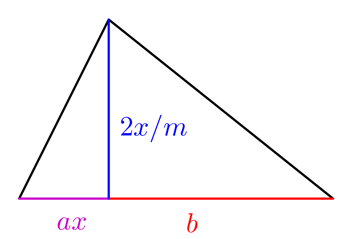
Nu er det ikke alle felter, der er kvadratiske. Lad os nu antage, at landmanden har en mere mærkeligt formet mark med to trekantede dele som vist til højre.
For passende værdier af  og
og 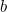 er den mængde afgrøde, som landmanden kan dyrke på denne mark, givet ved
er den mængde afgrøde, som landmanden kan dyrke på denne mark, givet ved
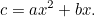 |
Dette ligner meget mere den kvadratiske ligning, som vi er vant til, og selv under skattemandens onde øje er den meget sværere at løse. Alligevel kom babylonierne med svaret igen. Først dividerer vi med  for at få
for at få
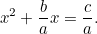 |
Nu fuldender vi kvadratet ved at bruge det faktum, at
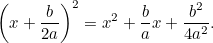 |
Ved at kombinere dette med den oprindelige ligning får vi
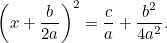 |
Dette er nu en ligning, som vi kan løse ved at tage kvadratrødder. Resultatet er den berømte “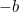 -formel”:
-formel”:
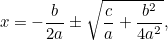 |
, som kan omskrives som
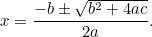 |
(Formlen har normalt “-4ac”, fordi den kvadratiske ligning mere normalt skrives i formen “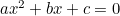 “.)
“.)
Den kendsgerning, at det at tage en kvadratrod kan give et positivt eller et negativt svar, fører til det bemærkelsesværdige resultat, at en kvadratisk ligning har to løsninger. Så meget for at matematiske gåder kun har én løsning!
Nu er det her, at undervisningen i kvadratiske ligninger ofte stopper. Vi er nået til det objekt, som alle journalister elsker, når de interviewer matematikere – en formel. Man kan finde på uendelige spørgsmål, som går ud på at sætte værdier af 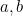 og
og  ind i formlen for at få (to) svar. Men det er slet ikke det, som matematikken handler om. At finde en formel er kun det første skridt på en lang vej. Vi er nødt til at spørge, hvad formlen betyder; hvad fortæller den os om universet; er det virkelig vigtigt at have en formel? Lad os nu se, hvor denne formel vil føre os hen.
ind i formlen for at få (to) svar. Men det er slet ikke det, som matematikken handler om. At finde en formel er kun det første skridt på en lang vej. Vi er nødt til at spørge, hvad formlen betyder; hvad fortæller den os om universet; er det virkelig vigtigt at have en formel? Lad os nu se, hvor denne formel vil føre os hen.
En overraskelse for grækerne, en smule matematisk origami og sans for proportioner
Vi spoler nu 1000 år frem til de gamle grækere og ser, hvad de gjorde ud af kvadratiske ligninger. Grækerne var fremragende matematikere og opdagede en stor del af den matematik, som vi stadig bruger i dag. En af de ligninger, som de var interesserede i at løse, var den (simple) kvadratiske ligning
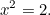 |

De vidste, at denne ligning havde en løsning. Faktisk er det længden af hypotenusen i en retvinklet trekant, som havde sider af længden 1.
Det følger af Pythagoras’ sætning, at hvis en retvinkletvinklet trekant har de kortere sider  og
og  og hypotenusen
og hypotenusen  så
så
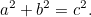 |
Sætter man 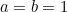 og
og  , så er
, så er 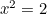 . Altså
. Altså 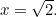
Sådan, hvad er  i dette tilfælde? Eller, for at stille det spørgsmål, som grækerne stillede, hvad er det for et tal? Grunden til, at dette havde betydning, lå i grækerens sans for proportioner. De mente, at alle tal stod i et rimeligt forhold til hinanden. For at være præcis betød det, at alle tal var brøker af formen
i dette tilfælde? Eller, for at stille det spørgsmål, som grækerne stillede, hvad er det for et tal? Grunden til, at dette havde betydning, lå i grækerens sans for proportioner. De mente, at alle tal stod i et rimeligt forhold til hinanden. For at være præcis betød det, at alle tal var brøker af formen 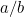 , hvor
, hvor  og
og  er hele tal. Tal som 1/2, 3/4 og 355/113 er alle eksempler på brøker. Det var naturligt at forvente, at
er hele tal. Tal som 1/2, 3/4 og 355/113 er alle eksempler på brøker. Det var naturligt at forvente, at  også var en brøk. Den store overraskelse var, at det ikke er det. Faktisk er
også var en brøk. Den store overraskelse var, at det ikke er det. Faktisk er
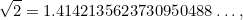 |
, hvor prikkerne  betyder, at decimaludvidelsen af
betyder, at decimaludvidelsen af  fortsætter til uendeligt uden noget synligt mønster. (Vi vil møde denne situation igen senere, når vi lærer om kaos.)
fortsætter til uendeligt uden noget synligt mønster. (Vi vil møde denne situation igen senere, når vi lærer om kaos.)
 var det første irrationelle tal (dvs. et tal, der ikke er en brøk, eller rationelt), der blev anerkendt som sådan. Andre eksempler omfatter
var det første irrationelle tal (dvs. et tal, der ikke er en brøk, eller rationelt), der blev anerkendt som sådan. Andre eksempler omfatter 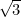 ,
,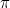 ,
,  og i virkeligheden “de fleste” tal. Det tog indtil det 19. århundrede, før vi havde en god måde at tænke over disse tal på. Opdagelsen af, at
og i virkeligheden “de fleste” tal. Det tog indtil det 19. århundrede, før vi havde en god måde at tænke over disse tal på. Opdagelsen af, at  ikke var et rationelt tal, vakte både stor begejstring (100 okser blev ofret som følge heraf) og et stort chok, idet opdageren måtte begå selvmord. (Lad dette være en frygtelig advarsel til de matematisk interesserede!) På dette tidspunkt opgav grækerne algebraen og gik over til geometri.
ikke var et rationelt tal, vakte både stor begejstring (100 okser blev ofret som følge heraf) og et stort chok, idet opdageren måtte begå selvmord. (Lad dette være en frygtelig advarsel til de matematisk interesserede!) På dette tidspunkt opgav grækerne algebraen og gik over til geometri.
Langt fra at være et obskurt tal møder vi  regelmæssigt: hver gang vi bruger et stykke A4-papir. I Europa måles papirstørrelser i A-størrelser, hvor A0 er det største med et areal på
regelmæssigt: hver gang vi bruger et stykke A4-papir. I Europa måles papirstørrelser i A-størrelser, hvor A0 er det største med et areal på 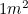 . A-størrelserne har et særligt forhold mellem dem. Hvis vi nu laver lidt origami, idet vi tager et ark A1-papir og derefter folder det på midten (langs den længste side), får vi A2-papir. Foldes det igen på midten, får vi A3, og igen får vi A4 osv. Papiret er imidlertid udformet således, at proportionerne for hver af A-størrelserne er de samme – det vil sige, at hvert stykke papir har samme form.
. A-størrelserne har et særligt forhold mellem dem. Hvis vi nu laver lidt origami, idet vi tager et ark A1-papir og derefter folder det på midten (langs den længste side), får vi A2-papir. Foldes det igen på midten, får vi A3, og igen får vi A4 osv. Papiret er imidlertid udformet således, at proportionerne for hver af A-størrelserne er de samme – det vil sige, at hvert stykke papir har samme form.
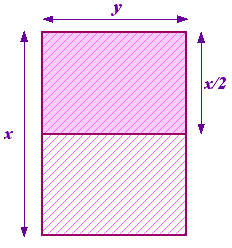
Vi kan stille spørgsmålet om, hvilke proportioner dette er. Start med et stykke papir med siderne x og y, hvor x er den længste side. Del nu dette i to, så du får et andet stykke papir med siderne y og x/2 med nu y som den længste side. Dette er illustreret til højre.
Proportionerne for det første stykke papir er 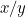 , og proportionerne for det andet er
, og proportionerne for det andet er 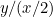 eller
eller 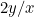 . Vi ønsker, at disse to proportioner skal være lige store. Det betyder, at
. Vi ønsker, at disse to proportioner skal være lige store. Det betyder, at
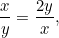 |
eller
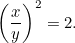 |
Endnu en kvadratisk ligning! Heldigvis er det en, som vi allerede har mødt. Når vi løser den, finder vi, at
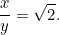 |
Dette resultat er let for dig at kontrollere. Du skal blot tage et ark A4- (eller A3- eller A5-) papir og måle siderne. Vi kan også regne størrelsen af hvert ark ud. Arealet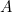 af et stykke A0-papir er givet ved
af et stykke A0-papir er givet ved
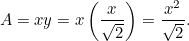 |
Men vi ved, at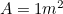 , så vi har en anden kvadratisk ligning for den længste side
, så vi har en anden kvadratisk ligning for den længste side af A0, givet ved
af A0, givet ved
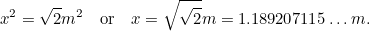 |
Dette betyder, at den længste side af A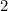 er givet ved
er givet ved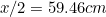 (hvorfor?) og den af A
(hvorfor?) og den af A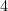 ved
ved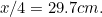 . Kontroller disse på dine egne ark papir.
. Kontroller disse på dine egne ark papir.
Papir, der bruges i USA, og som kaldes foolscap, har et andet forhold. For at se hvorfor, vender vi tilbage til grækerne og en anden kvadratisk ligning. Efter at have forårsaget så megen sorg forløser den kvadratiske ligning sig selv i jagten på de perfekte proportioner: en søgen, der fortsætter i dag i udformningen af filmscener og kan ses i mange aspekter af naturen.
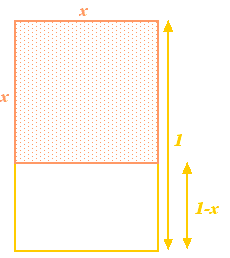
Lad os starte med et rektangel og derefter fjerne et kvadrat fra det med samme sidelængde som den korteste side af rektanglet. Hvis den længste side af rektanglet har længden 1 og den korteste side har længden  , så har kvadratet sider af længden
, så har kvadratet sider af længden  . Hvis man fjerner det fra rektanglet, får man et mindre rektangel med den længste side
. Hvis man fjerner det fra rektanglet, får man et mindre rektangel med den længste side  og den mindste side
og den mindste side 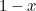 . Så langt, så abstrakt. Grækerne mente imidlertid, at det rektangel, der havde de mest æstetiske proportioner (det såkaldte gyldne rektangel), var det rektangel, for hvilket det store og det lille rektangel, der er konstrueret ovenfor, har de samme proportioner. For at dette er muligt, skal vi have
. Så langt, så abstrakt. Grækerne mente imidlertid, at det rektangel, der havde de mest æstetiske proportioner (det såkaldte gyldne rektangel), var det rektangel, for hvilket det store og det lille rektangel, der er konstrueret ovenfor, har de samme proportioner. For at dette er muligt, skal vi have
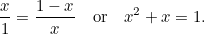 |
Dette er endnu en kvadratisk ligning: en meget vigtig ligning, der dukker op i alle mulige anvendelser. Den har den (positive) løsning
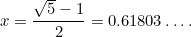 |
Tallet  kaldes det gyldne snit og betegnes ofte med det græske bogstav
kaldes det gyldne snit og betegnes ofte med det græske bogstav 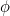 .
.

Det gyldne rektangel kan ses i formen på vinduer, især på georgianske huse. I nyere tid kan man også finde det gyldne snit som den “perfekte form” for fotografier og filmbilleder. Den kvadratiske ligning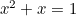 optræder også i undersøgelser af kaninpopulationer og i det mønster, som frøene i solsikker og bladene på planternes stængler er anbragt i. Disse er alle forbundet med det gyldne snit gennem Fibonacci-sekvensen, som er givet ved
optræder også i undersøgelser af kaninpopulationer og i det mønster, som frøene i solsikker og bladene på planternes stængler er anbragt i. Disse er alle forbundet med det gyldne snit gennem Fibonacci-sekvensen, som er givet ved
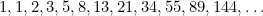 |

Solsikkekerner, arrangeret ved hjælp af Fibonacci-tallene |
Parthenon, der legemliggør det gyldne snit |
I denne rækkefølge er hvert udtryk summen af de to foregående udtryk. Fibonacci opdagede det i det 15. århundrede i et forsøg på at forudsige den fremtidige bestand af kaniner. Hvis man tager forholdet mellem hvert udtryk og det efterfølgende, får man talrækken
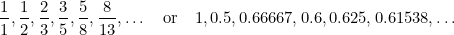 |
, og disse tal kommer tættere og tættere på (du gættede det) det gyldne snit 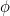 .
.
Ved at finde begge rødderne i ovenstående kvadratiske ligning kan vi faktisk finde en formel for det niende udtryk i Fibonacci-sekvensen. Hvis  er det
er det 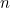 te sådanne tal med
te sådanne tal med 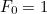 og
og 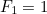 , så er
, så er  givet ved formlen
givet ved formlen
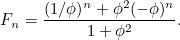 |
Konikken forbinder kvadratiske ligninger med stjernerne

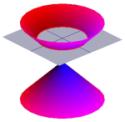
Grækerne var også meget interesserede i keglernes form. billedet til venstre viser en typisk kegle.
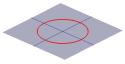
Halvdelen af keglen kan visualiseres som spredningen af det lys, der kommer fra en fakkel. Hvis man nu lyser med en lommelygte på en flad overflade som f.eks. en væg, vil man se forskellige former, når man bevæger lommelygten rundt. Disse former kaldes keglesnit og er de kurver, som man får, hvis man skærer et snit gennem en kegle i forskellige vinkler. Netop disse kurver blev studeret af grækerne, og de erkendte, at der grundlæggende var fire typer af keglesnit. Hvis man tager et vandret snit gennem keglen, får man en cirkel. Et snit i en lille vinkel i forhold til vandret giver en ellipse. Hvis man tager et lodret snit, får man en hyperbel, og hvis man tager et snit parallelt med den ene side af keglen, får man en parabel. Disse kurver er illustreret nedenfor.
 |
 |
 |
 |
 |
 |
 |
 |

Et krydssnit af en kegle kan være en cirkel … |

… en ellipse … |
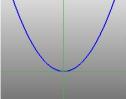
… en parabel … |
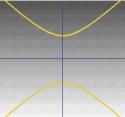
… eller en hyperbel. |
Koniske snit kommer ind i vores historie, fordi hvert af dem beskrives af en kvadratisk ligning. Især hvis 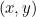 repræsenterer et punkt på hver kurve, så forbinder en kvadratisk ligning
repræsenterer et punkt på hver kurve, så forbinder en kvadratisk ligning  og
og 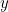 . Vi har:
. Vi har:
Cirklen: 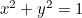 ;
;
Ellipsen: 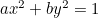 ;
;
Hyperbolaen: 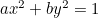 ;
;
: 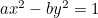 ;
;
Parablen: 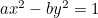 ;
;
Parablen: 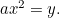
Disse kurver har været kendt og studeret siden grækerne, men bortset fra cirklen syntes de ikke at have nogen praktisk anvendelse. Men som vi skal se i næste nummer af Plus, førte en forbindelse mellem kvadratiske ligninger og kegleformede kurver sammen med en mægtig heldig tilfældighed til en forståelse af den måde, universet fungerede på, og i det 16. århundrede kom tiden for kegleformede kurver til at ændre verden.
Om forfatterne
Chris Budd er professor i anvendt matematik ved Institut for Matematiske Videnskaber ved University of Bath og professor i matematik ved Royal Institution i London.
Chris Sangwin er ansat ved School of Mathematics and Statistics ved University of Birmingham. Han er Research Fellow i Learning and Teaching Support Network centre for Mathematics, Statistics and Operational Research.
De har for nylig skrevet den populære matematikbog Mathematics Galore!, der er udgivet af Oxford University Press.
Denne artikel er til dels inspireret af en bemærkelsesværdig debat i det britiske underhus om kvadratiske ligninger. Referatet af denne debat kan findes i Hansard, United Kingdom House of Commons, 26. juni 2003, Columns 1259-1269, 2003, som er tilgængelig online på House of Commons Hansard Debate website.