En viktig fråga är hur primtalen är fördelade bland de hela talen. Svaret är, med några få ord, ganska slumpmässigt, med tanke på viss grundläggande statistik…
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman
| |
|
Introduktion
För många år sedan gissades det att det finns ett oändligt antal par av primtalen $p$, $q$ med $q = p+2$. Det har gjorts en del färska (och berömda) framsteg i fråga om detta problem. Jag kommer att säga lite om de senaste framstegen och istället diskutera vad vi förväntar oss – snarare än vad vi vet – om sådana par. Inget jag kommer att säga är nytt, och jag har till viss del bara utvecklat vad Andrew Granville säger i sin nyligen publicerade exposé om de senaste framstegen.
Hur många primtal förväntar vi oss?
Ett primtal är ett positivt heltal som inte har några divisorer utom sig självt och $1$. Definitionen är enkel, men så snart man börjar utforska betydelsen av primtal inser man att de uppvisar ett mycket subtilt beteende. En viktig fråga är hur primtalen är fördelade bland de hela talen. Svaret är, med några få ord, ganska slumpmässigt, med tanke på viss grundläggande statistik. Vad menar jag med detta?
Nja, här är en kvadratisk matris som avbildar alla primtal upp till $400$:

Det finns vissa mönster i denna matris, varav jag kommer att kommentera några senare. De flesta av dem du uppfattar orsakas av någon artefakt i displayen. Till exempel är varannan kolumn i princip tom, och det beror på att det enda jämna primtalet är $2$. Dessutom är var femte kolumn i princip tom. Mer intressanta är de dubbla primtalsparen (varav vissa inte är så synliga eftersom de delas upp i två rader, t.ex. $59$, $61$), och även vissa mönster som är relaterade till de sista siffrorna som visas. Dessa är vad man skulle kunna kalla lokala mönster. Det finns inga globala mönster som är uppenbara.
Det har lagts ner mycket arbete på extremt effektiva sätt att framställa primtal, men nuförtiden tar även ett mycket enkelt program bara lite tid på sig för att göra stora listor med primtal. Ett av de mest fruktbara programmen gör en stor lista med primtal och använder sedan denna för att beräkna funktionen $\pi(n)$, antalet primtal $\le n$.
En sak som detta kan användas till är att få en ungefärlig uppfattning om frekvensen av primtal. Det finns 135$ primtal i intervallet $$:
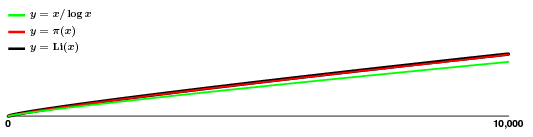
Närmningen ser bra ut! Så även om $\pi(x)$ studsar runt lite, till synes utan något större mönster, har vi en ganska bra uppskattning för det, vilket innebär att vi har en bra uppfattning om hur primtalen växer, åtminstone i genomsnitt.
Det bör dock hållas i åtanke att den skenbara jämnheten är bedräglig. Närmare bestämt ser de två översta kurvorna ut så här:

Kommentarer?
Heuristiskt resonemang om tvillingprimtal
Twillingprimtal är ett par $p$, $p+2$ som båda är primtal. Från en av diagrammen ovan ser vi till exempel tvillingprimerna $$ , , , , , , , $$
och andra. Man har antagit att det finns ett oändligt antal av dem, men även om det finns många empiriska bevis för detta har det ännu inte bevisats.
Det kanske starkaste beviset är en formel som approximerar antalet $\pi_{2}(x)$ av tvillingprimtal $\le x$ anmärkningsvärt väl. Jag är inte helt säker på formelns ursprung, men den dök först upp i en artikel av G. H. Hardy och J. E. Littlewood (själva ett par tvillingprimes) från 1923. Papperet innehåller flera liknande formler, alla baserade på samma metod, som de hade använt för att angripa många problem tidigare. Detta var deras cirkelmetod. Deras härledning av formeln för $\pi_{2}(x)$ är inte alls rigorös, men den är mycket övertygande. Det finns en kortfattad redogörelse för detta i en bilaga till Andrew Granvilles artikel.
Men strax efter andra världskriget föreslog Lord Cherwell (Frederick Lindemann) en mer elementär probabilistisk (och fortfarande inte rigorös) härledning. Detta ledde till ett samarbete med E. M. Wright och slutligen till en postum gemensam publikation. Detta förklaras i avsnitt 22.20 i Hardys och Wrights välkända text. En något mer elementär version av detta finns också i en bilaga till Granvilles artikel (avsnitt 2.5). Jag följer honom.
Utgångspunkten för det rimliga resonemanget är vår uppskattning av $\pi(x)$, antalet primtal mindre än eller lika med $x$. Grundtanken i härledningen är att primtalen i stor utsträckning är slumpmässigt fördelade. Vi vet att i närheten av $x$ är tätheten av primtal ungefär $1/\log x$. Om primtalen fördelades slumpmässigt skulle sannolikheten för att två givna tal i närheten av $x$ är primtal bara vara produkten av de lokala sannolikheterna, vilket är $1/\log^{2} x$. Detta är verkligen ett falskt resonemang, eftersom om $n > 2$ är sannolikheten att både $n$ och $n+1$ är primtal 0$, medan det faktum att $p$ är ett primtal tycks öka chansen att $p+2$ är ett primtal. Det finns liknande överväganden att ta hänsyn till på grund av eventuell delbarhet genom andra små primtal också i närheten av $x$.
Det finns ett enkelt faktum i den här historien. Om $q$ är ett valfritt primtal är sannolikheten för att slumpmässigt välja ett heltal som inte är delbart med $q$ 1-1/q$. Sannolikheten att välja två som inte är delbara med $q$ är alltså produkten $(1 – 1/q)^{2}$. Anta att $p$ och $p+2$ båda är primtal, då är varken $p$ eller $p+2$ delbart med $q$. Om $q = 2$ sker detta 1/2$ gånger. Om $q \ne 2$ är sannolikheten för att $p \not\equiv 0$ och $p \not\equiv -2$ modulo $q$ $(1 – 2/q)$. På grund av Chinese Remainder Theorem är delbarhet med två primtal en oberoende händelse. Så om $x$ är stort och $Q$ är relativt litet är sannolikheten för att ett talpar $m$ och $n$ i närheten av $x$ inte är en multipel av något primtal upp till $Q$ $$ $$ { 1\over 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} } \, . $$
Låt $\Gamma_{Q}$ vara förhållandet mellan detta och $\prod_{q \le Q}(1 – 2/q)$: $$ \Gamma_{Q} = { 1\över 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} \over (1 – 2/q) } $$ Vi har $$ { 1 – 2/q \over (1-1/q)^{2} } = { (1 – 1/q)^{2} – 1/q^{2} \over (1 – 1/q)^{2} } = 1 – { 1 \over (q -1)^{2} } \, . $$ Ett standardkriterium säger att denna produkt konvergerar om summan $\sum 1/(q-1)^{2}$ konvergerar. Men den konvergerar eftersom integraltestet säger oss att $\sum 1/n^{2}$ konvergerar. Därför konvergerar denna produkt faktiskt till ett tal $\Pi_{\infty}$ som $Q \rightarrow \infty$. Låt $C_{2}$ vara dess inversa. I avsnitt 2.5 i Granvilles artikel står det att det borde vara intuitivt rimligt vid denna tidpunkt att antalet $\pi_{2}(x)$ av tvillingprimer $\le x$ approximeras genom $$ \$Pi_{2}(x) = C_{2} \int_{2}^{\infty} { dx \over \log^{2} x } \, . $$
Texterna av Hardy och Wright innehåller en noggrannare analys som gör det intuitiva språnget lite tydligare.
Värdet på konstanten här beräknades för länge sedan av J. W. Wrench till ungefär 1 dollar.320323236316969373914785562422002911155686525 \ldots $. Här är en jämförelse av några värden på $\pi_{2}(x)$ och formeln i intervallet $$: $$ \matrix{ n & 10 000 & 20 000 & 30 000 & 40 000 & 50 000 \cr \pi_{2}(n) & 205\phantom{.0} & 342 \phantom{.0} & 467 \phantom{.0} & 591 \phantom{.0} & 705 \phantom{.0} & \cr \Pi_{2}(x) & 214.2 & 357.7 & 486.7 & 607.4 & 722.5 \cr } $$ $$ $$ \matrix{ n & 60 000 & 70 000 & 80 000 & 90 000 & 100 000 \cr \pi_{2}(n) & 811 \phantom{.0} & 905 \phantom{.0} & 1007 \phantom{.0} & 1116 \phantom{.0} & 1224\phantom{.0} \cr \Pi_{2}(x) & 833.3 & 940.9 & 1045.7 & 1148.2 & 1248.7 \cr } $$
Kommentarer?
Dicksons gissning
Twillingprimer är ett specialfall av något mycket mer allmänt. Man kan fråga sig om det finns ett oändligt antal par $p$, $p+4$ eller $p$, $p+6$ som är primtal? Eller $p$, $p+10$? Fallet med $p$ och $p+10$ antyds säkert av en av bilderna ovan, där sådana par är lätt synliga. Vad sägs om tripplar av något slag? Anta att $a_{1}$, $a_{2}$, $\ldots$ , $a_{k}$ utgör en matris av heltal. Kan vi förvänta oss att det finns ett oändligt antal uppsättningar $n+a_{1}$, $n+a_{2}$, $\ldots$ , $n+a_{k}$ som alla är primtal?
Man måste vara lite försiktig. Det finns inga primtalspar av formen $p$, $p+1$ (tidigare $p = 2$), eftersom ett av dessa två tal måste vara delbart med $2$. På samma sätt finns det efter $p = 3$ inga primtalstjärnor $p$, $p+2$, $p+4$ eftersom ett av dessa måste vara delbart med $3$.
Detta sista exempel borde vara upplysande. Talet $p+4$ är delbart med $3$ om och endast om $p+1$ är delbart med $3$. Därför delar $3$ något av talen $p$, $p+2$, $p+4$ om och endast om det delar $p$, $p+1$, $p+2$. Men detta är säkert, eftersom den sista trippeln tydligt täcker alla tal modulo $3$.
I allmänhet sägs $p$ vara ett hinder för matrisen $(a_{i})$ om $p$ alltid delar minst ett av varje sekvens $n+a_{i}$ ($i = 1$, $\ldots$, $k$). Detta sker om och endast om talen $a_{i} \; {\rm mod} \, p$ fyller hela $Z/p$.
Detta kan aldrig ske om $p > k$, så för att kontrollera om något $p$ hindrar $(a_{i})$ behöver vi bara kontrollera om $a_{i}$ täcker $Z/p$ för alla $p \le k$. Vi kallar matrisen $(a_{i})$ godtagbar om den inte har några primtalshinder.
Till exempel är $(1,3,7,9)$ en godtagbar matris, eftersom, vilket du enkelt kan kontrollera, varken $2$ eller $3$ är ett hinder. Flera primsekvenser som passar in i detta mönster kan ses i ett av diagrammen ovan. Andra exempel är (a) alla $0$, $2n$; (b) $0$, $4$, $6$; (c) $0$, $2$, $6$.
Det finns godtyckligt stora godtagbara mängder. Faktum är:
Theorem. Om $a_{1}$ till $a_{k}$ är någon uppsättning av distinkta primtal $> k$, utgör de en godtagbar uppsättning.
Varför detta? Om $p$ är ett valfritt primtal där $p> k$, har vi redan sett att det inte kan vara ett hinder. Men om $p \le k$ kan den inte dela någon av de $a_{i}$, varav ingen kan vara kongruent med $0$ modulo $p$. Så $a_{i}$ fyller inte $Z/p$.
Ett specialfall av en gissning som ursprungligen gjordes av L. E. Dickson är att om det inte finns några primära hinder för $(a_{i})$ så finns det ett oändligt antal primära sekvenser av formen $(n +a_{i})$.
Vad har hänt nyligen
Det här är inte rätt ställe att berätta hela historien, som har behandlats grundligt på andra ställen. Jag rekommenderar särskilt Quanta-artikeln av Erica Klarreich för en populär redogörelse och Granvilles uppsats för en mer teknisk redogörelse. Jag vill bara ange lite mer exakt än i Klarreichs redogörelse vad det mest kända av de nya resultaten är.
Det beror på Yitang Zhang. Det enklaste uttalandet av vad han bevisade är att det finns ett oändligt antal intervaller $[n, n+70 000 000)$ som innehåller minst två primtal. Detta är svagare än den förmodade tvillingprimesiffran, men ligger begreppsmässigt mycket nära den. I senare arbeten (av många matematiker) har gapets storlek minskats kraftigt, men det finns förmodligen inget sätt att minska det till 2 dollar med nuvarande metoder.
Som Granville förklarar är Zhangs första och förmodligen viktigaste resultat att det finns $k$ med egenskapen att om $a_{1}$, $\ldots$ , $a_{k}$ är en godtagbar mängd med $k$ element, så finns det ett oändligt antal $n$ så att $\{ n +a_{i} \}}$ innehåller minst två primtal. (I Klarreichs Quanta-artikel kallas matrisen för en ”kam”. Kom ihåg att enligt Dicksons gissning skulle vi förvänta oss att kunna säga att alla $k$ är primtal). Faktum är att Zhang bevisade att detta påstående är sant för ett visst $k =3 500 000$ som sträcker sig över ett intervall på $70 000 000$. Den numera berömda konsekvensen är för vissa $m \lt 70 000 000$ att det finns ett oändligt antal primtalpar $p$, $p+m$.
Läs vidare
- Lord Cherwell och E. M. Wright, ”The frequency of prime patterns”, The Quarterly Journal of Mathematics 11 (1960).
De som vet något om Lord Cherwells liv, även känd som Frederick Lindemann, kommer att bli mycket förvånade över att få reda på hans bidrag till talteorin. Wikipedias biografi antyder inte på ett adekvat sätt alla orsakerna till hans dåliga rykte som Churchills främsta vetenskapliga rådgivare under andra världskriget.
- L. E. Dickson, ”A new extension of Dirichlet’s theorem on prime numbers”, Messenger of Mathematics 33.
Se även Wikipedias artikel om Dicksons gissning.
- Andrew Granville, ”Primes in intervals of bounded length”. Finns på hans hemsida.
- G. H. Hardy, Ramanujan, Cambridge University Press.
Avsnitt 2.5 innehåller en idealisk härledning av en möjlig formel för $\pi(x)$.
- G. H. Hardy och J. E. Littlewood, ”Some problems of ’Partitio numerorum’ III: on the expression of a number as a sum of primes”, Acta Mathematica 44 (1923).
- G. H. Hardy and E. M. Wright, The theory of numbers, Oxford Press.
- Erica Klarreich, ”Together and alone, closing the prime gap”, Quanta November 19, 2013.
- B. Riemann, ”Om antalet primtal som är mindre än en given mängd”. En engelsk översättning av denna klassiker av David Wilkins finns tillgänglig via en länk i Wikipedia.
Denna skisserar bland annat en härledning av den ungefärliga formeln för $\pi(x)$.
- J. W. Wrench, ”Evaluation of Artin’s constant and the twin-prime constant”, Mathematics of Computation 76 (1961).
En tidig beräkning av $C_{2}$.
- Listor över primtal upp till 1 000 000 000 000 000 000$
- En lista över de första 20 000 tvillingprimtalen.
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman