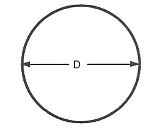
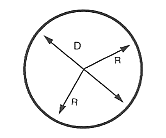
Diameter på en cirkel
Diametern på en cirkel eller ett klot är lika med två gånger radien.
$\text ”Diameter” = 2 ⋅ \text ”Radius”$
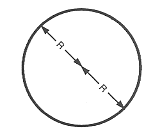
Cirkelns omkrets
Cirkelns eller sfärens omkrets är lika med 6,2832 gånger radien.
$\text ”Omkrets” = 6,2832 ⋅ R$
$C = 2 ⋅ π ⋅ R$
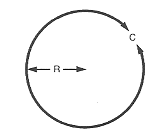
En cirkels eller sfärs omkrets är lika med 3,1416 gånger diametern.
$\text ”Omkrets” = 3.1416 ⋅ \text ”Diameter”$
$C = π ⋅ D$
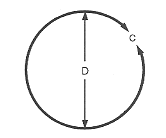
Radius av en cirkel
Radius av en cirkel eller ett klot är lika med diametern dividerad med 2.
$R = D / 2$
En cirkels area
En cirkels area är lika med cirkelns radie multiplicerat med radien och sedan detta tal multiplicerat med 3,1416.
$\text ”Area” = R^2 ⋅ π$
$\text ”Area” = R ⋅ R ⋅ R ⋅ 3,1416$
Detta tal kommer att vara i kvadrattum eller kvadratmillimeter, beroende på vilket mätsystem som används.
En cirkels area är lika med cirkelns diameter multiplicerad med diametern och sedan detta tal multiplicerat med 3,1416 och sedan divideras denna summa med 4.
$\text ”Area” = D ⋅ D ⋅ 3.1416 / 4$
$\text ”Area” = D^2 ⋅ π/ 4$
Area av en cylinder
Detta tal kommer att vara i kvadrattum eller kvadratmillimeter, beroende på vilket mätsystem som används.
En cylinders area är lika med 6,2832 ( 2 × π) gånger cylinderns radie, gånger summan av radien plus höjden.
$\text ”Area” = 2 ⋅ 3.1416 ⋅ R ⋅ R ⋅ ( R + H )$
$\text ”Area” = 2 ⋅ π ⋅ R ⋅ R ⋅ ( R + H )$
Detta tal kommer att anges i kvadrattum eller kvadratmillimeter, beroende på vilket mätsystem som används.
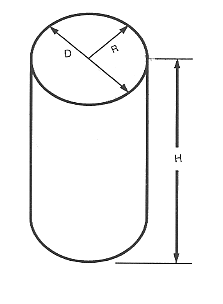
Cylinderns volym
Cylinderns volym är lika med cylinderns radie multiplicerad med radien, och detta tal multiplicerat med 3,1416, och sedan multipliceras detta tal med längden av cylindern.
$\text ”Volym” = 3.1416 ⋅ R ⋅ R ⋅ H$
$\text ”Volym” = π ⋅ R^2 ⋅ H$
Detta tal kommer att anges i kubiktum eller kubikmillimeter, beroende på vilket mätsystem som används.
Area av en sfär
Area av en sfär är lika med kvadraten på sfärens radie multiplicerat med 12,566 ( 4 × π) eller Pi gånger diametern i kvadrat ( π × D × D ).
$\text ”Area” = 12.566 ⋅ R ⋅ R$
$\text ”Area” = 4 ⋅ π ⋅ R^2$
$\text ”Area” = π ⋅ D^2$
Detta tal kommer att vara i kvadrattum eller kvadratmillimeter, beroende på vilket mätsystem som används.
Volym av en sfär
Volymen av en sfär är lika med sfärens radie, multiplicerat med radien igen. Sedan multipliceras detta tal med radien igen. Sedan multipliceras detta tal med 12,566. och resultatet divideras med 3.
$\text ”Volym” = 12.566 ⋅ R ⋅ R ⋅ R ⋅ R / 3$
$\text ”Volym” = 4 ⋅ π ⋅ R ⋅ R ⋅ R ⋅ R / 3$
$text ”Sfärvolym” = 4/3 ⋅ π ⋅ r^3 = ( π ⋅ d^3)/6$
Detta tal kommer att anges i kubikcentimeter eller kubikmillimeter, beroende på vilket mätsystem som används.