De olika typerna av styrsystem används för att förbättra styrsystemens prestanda. I det här kapitlet kommer vi att diskutera de grundläggande regulatorerna såsom proportionella, derivativa och integrala regulatorer.
Proportionell regulator
Den proportionella regulatorn producerar en utgång, som är proportionell mot felsignalen.
$$$u(t) \propto e(t) $$
$$\Rightarrow u(t)=K_P e(t)$$
Applicera Laplacetransformationen på båda sidor –
$$$U(s)=K_P E(s)$$
$$\frac{U(s)}{E(s)}=K_P$$$
Därmed, är överföringsfunktionen för den proportionella regulatorn $K_P$.
Varvid,
U(s) är Laplace-transformen av manöversignalen u(t)
E(s) är Laplace-transformen av felsignalen e(t)
KP är proportionalitetskonstanten
Blockdiagrammet för det enhetsregleringssystem med negativ återkoppling och sluten slinga tillsammans med den proportionella regulatorn visas i följande figur.
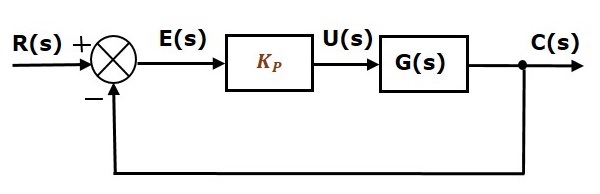
Den proportionella regulatorn används för att ändra den transienta responsen enligt kraven.
Derivativa regulatorn
Den derivativa regulatorn producerar en utgång som är derivat av felsignalen.
$$$u(t)=K_D \frac{\text{d}e(t)}{\text{d}t}}$$$
Applicera Laplacetransformationen på båda sidor.
$$$U(s)=K_D sE(s)$$
$$\frac{U(s)}{E(s)}=K_D s$$$
Därmed är överföringsfunktionen för den derivativa regulatorn $K_D s$.
Varvid $K_D$ är den derivativa konstanten.
Blockdiagrammet för det slutna styrsystemet med negativ återkoppling med enhetlig negativ återkoppling tillsammans med den derivativa regulatorn visas i följande figur.
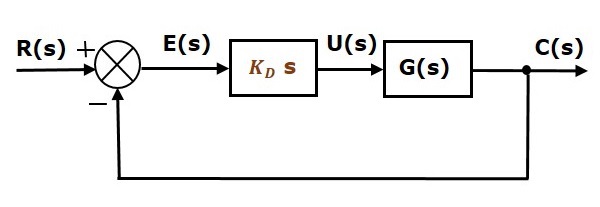
Derivatregulatorn används för att göra det instabila reglersystemet till ett stabilt.
Integralregulator
Integralregulatorn producerar en utgång, som är integral av felsignalen.
$$$u(t)=K_I \int e(t) dt$$$
Applicera Laplacetransformationen på båda sidorna –
$$$U(s)=\frac{K_I E(s)}{s}$$
$$\frac{U(s)}{E(s)}=\frac{K_I}{s}$$$
Därför, är överföringsfunktionen för den integrala regulatorn $\frac{K_I}{s}$.
Varvid $K_I$ är den integrala konstanten.
Blockdiagrammet för det slutna reglersystemet med enhets negativ återkoppling tillsammans med integralregulatorn visas i följande figur.
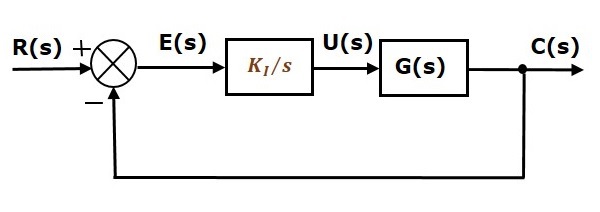
Integralregulatorn används för att minska det stationära felet.
Låt oss nu diskutera kombinationen av grundläggande regulatorer.
Proportionalderivatregulator (PD)
Proportionalderivatregulatorn producerar en utgång som är en kombination av utgångarna från proportional- och derivatregulatorn.
$$$u(t)=K_P e(t)+K_D \frac{\text{d}e(t)}{\text{d}t}}$$$
Applicera Laplacetransformationen på båda sidor –
$$$U(s)=(K_P+K_D s)E(s)$$
$$\frac{U(s)}{E(s)}=K_P+K_D s$$
Därför, är överföringsfunktionen för den proportionella derivatregulatorn $K_P + K_D s$.
Blockdiagrammet för det slutna reglersystemet med enhets negativ återkoppling tillsammans med den proportionella derivatregulatorn visas i följande figur.
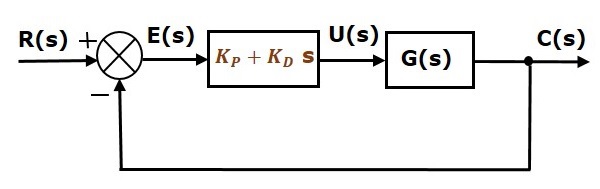
Den proportionella derivatregulatorn används för att förbättra stabiliteten hos reglersystemet utan att påverka steady state-felet.
Proportionell-integral (PI)-regulator
Den proportionella-integralregulatorn producerar en utgång, som är kombinationen av utgångarna från proportionella- och integralregulatorn.
$$$u(t)=K_P e(t)+K_I \int e(t) dt$$$
Applicera Laplacetransformationen på båda sidor –
$$$U(s)=\left(K_P+\frac{K_I}{s} \right )E(s)$$
$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}$$
Därför, är överföringsfunktionen för den proportionella integralregulatorn $K_P + \frac{K_I} {s}$$.
Blockdiagrammet för det slutna reglersystemet med negativ återkoppling med enhet tillsammans med den proportionella integralregulatorn visas i följande figur.
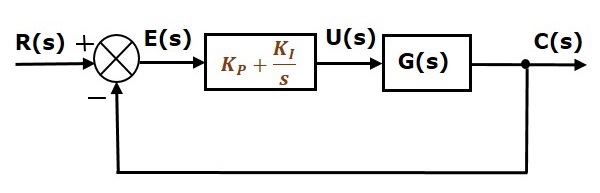
Den proportionella integralregulatorn används för att minska det stationära felet utan att påverka reglersystemets stabilitet.
Proportionell integralderivatregulator (PID-regulator
Den proportionella integralderivatregulatorn producerar ett utlopp, som är kombinationen av utgångarna från proportionell-, integral- och derivatregulatorn.
$$$u(t)=K_P e(t)+K_I \int e(t) dt+K_D \frac{\text{d}e(t)}{\text{d}t}}$$$
Applicera Laplacetransformationen på båda sidor –
$$$U(s)=\left(K_P+\frac{K_I}{s}+K_D s \right )E(s)$$
$$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}+K_D s$$
Därför, är överföringsfunktionen för den proportionella integralavledningsregulatorn $K_P + \frac{K_I} {s} + K_D s$.
Blockdiagrammet för det slutna reglersystemet med negativ återkoppling med enhet tillsammans med den proportionella integralavledningsregulatorn visas i följande figur.
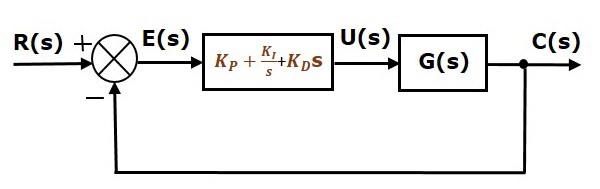
Den proportionella integralavledningsregulatorn används för att förbättra stabiliteten hos reglersystemet och för att minska steady state-felet.