Låt oss börja med att undersöka division av värden med exponenter.
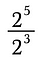
Visst du att exponenter representerar upprepad multiplikation? Så vi kan skriva om ovanstående uttryck som:
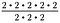
Då 2/2 = 1, upphäv tre uppsättningar av 2/2. Då återstår 2 – 2, eller 2 i kvadrat.
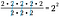
Självklart kan vi ta en genväg och subtrahera antalet 2:or i botten från antalet 2:or i toppen. Eftersom dessa mängder representeras av sina respektive exponenter behöver vi bara skriva den gemensamma basen med skillnaden i exponentvärden som potens.
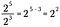
Om vi generaliserar denna regel får vi följande där n representerar ett reellt tal som inte är noll och x och y också är reella tal.
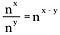
Utforskande av nollpotensen
Härifrån är det lätt att härleda förklaringen till varför ett tal som inte är noll och som höjs till nollpotensen är lika med 1. Låt oss återigen titta på ett konkret exempel.
Vi vet att varje tal som inte är noll dividerat med sig självt är lika med 1. Så jag kan skriva följande:
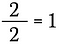
Detta är samma sak som att skriva:
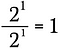
Nu ska jag använda exponentregeln från ovan för att skriva om vänstersidan av denna ekvation.
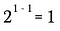
Detta är naturligtvis likvärdigt med:
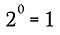
Vi kan använda samma process som i det här exemplet, tillsammans med den generaliserade regeln ovan, för att visa att alla reella tal som inte är noll och som är upphöjda till nollpotens måste resultera i 1.
Hur är det med noll till nollpotens?
Det är här det blir knepigt. Ovanstående metod går inte att använda eftersom det naturligtvis är förbjudet att dividera med noll. Låt oss undersöka varför.
Vi börjar med att titta på en vanlig delning med noll FEL.
Hur är det med 2÷0? Låt oss undersöka varför vi inte kan göra detta.
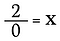
Division är egentligen bara en form av multiplikation, så vad händer om jag skriver om ovanstående ekvation som:
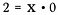
Vilket värde skulle kunna uppfylla denna ekvation för x?
Det finns inget värde! Alla tal gånger noll resulterar i noll, det kan aldrig vara lika med 2. Därför säger vi att division med noll är odefinierad. Det finns ingen möjlig lösning.
Nu tittar vi på 0÷0.
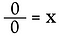
Också här skriver vi om det som ett multiplikationsproblem.
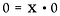
Här möter vi en mycket annorlunda situation. Lösningen för x skulle kunna vara VÅRT verkligt tal! Det finns inget sätt att bestämma vad x är. Därför anses 0/0 vara obestämt*, inte odefinierat.
Om vi försöker använda ovanstående metod med noll som bas för att bestämma vad noll i nollpotens skulle vara, stannar vi omedelbart upp och kan inte fortsätta eftersom vi vet att 0÷0 ≠ 1, men är obestämt.
Så vad är noll i nollpotens lika med?
Detta är mycket omdiskuterat. Vissa anser att det bör definieras som 1 medan andra anser att det är 0, och vissa anser att det är odefinierat. Det finns goda matematiska argument för var och en av dem, och kanske är det mest korrekt att betrakta den som obestämd.
Trots detta är det matematiska samfundet för att definiera noll i nollpotens som 1, åtminstone för de flesta syften.
Kanske är en användbar definition av exponenter för amatörmatematikern följande: