Matematikmodellering

Vissa funktioner är styckevis definierade. I det här avsnittet kommer vi att lära oss hur man definierar och graferar funktioner som i huvudsak är samlingar av diskreta bitar. Exempel på något som definieras på detta sätt är att utforma en bils profil, räkna ut ditt mobiltelefonabonnemang och beräkna inkomstskattesatser. Din skattesats beror till exempel på din inkomst och är densamma för en rad olika inkomster, vilket visas i tabellen nedan:

En styckevis funktion är en funktion där mer än en formel används för att definiera utgången över olika delar av området.

Vi använder styckevisa funktioner för att beskriva situationer där en regel eller ett förhållande ändras när ingångsvärdet passerar vissa ”gränser”. Vi stöter till exempel ofta på situationer i näringslivet där kostnaden per styck av en viss artikel rabatteras när antalet beställda överstiger ett visst värde. Skatteklämmor är ett annat verkligt exempel på styckevisa funktioner. Tänk t.ex. på ett enkelt skattesystem där inkomster upp till 10 000 dollar beskattas med 10 % och där alla ytterligare inkomster beskattas med 20 %. Skatten på en total inkomst, S, skulle vara 0,1S om S\le 10 000 dollar och 1000 + 0,2 (S – 10 000 dollar), om S> 10 000 dollar.

Utvärdera en styckevis definierad funktion

I det första exemplet kommer vi att visa hur man utvärderar en styckevis definierad funktion. Observera att det är viktigt att uppmärksamma domänen för att avgöra vilket uttryck som ska användas för att utvärdera inmatningen.

I följande video visar vi hur man utvärderar flera värden givet en styckevis definierad funktion.

I nästa exempel visar vi hur man utvärderar en funktion som modellerar kostnaden för dataöverföring för ett telefonbolag.

Analys av lösningen

Funktionen representeras i grafen nedan. Vi kan se var funktionen övergår från en konstant till en linje med positiv lutning vid g=2. Vi plottar graferna för de olika formlerna på en gemensam uppsättning axlar och ser till att varje formel tillämpas på sitt rätta område.

C(g) = C\left(g\right)=\begin{cases}{25}\text{ if }{ 0 }<{ g }<{ 2 }\\ 10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

Skriv en styckevis definierad funktion

I det sista exemplet ska vi visa hur man skriver en styckevis definierad funktion som modellerar priset för en guidad museibesök.

Analys av lösningen

Funktionen är representerad i Figur 21. Grafen är en diagonal linje från n=0 till n=10 och en konstant därefter. I det här exemplet stämmer de två formlerna överens vid mötespunkten där n=10, men alla styckevisa funktioner har inte den egenskapen.

I följande video visar vi ett exempel på hur man skriver en styckevis definierad funktion givet ett scenario.

Grafera styckevisa funktioner

I det här avsnittet ska vi grafera styckevisa funktioner. Funktionen som plottas nedan representerar kostnaden för att överföra data för ett visst mobiltelefonföretag. Vi kan se var funktionen övergår från en konstant till en linje med positiv lutning vid g=2. När vi plottar styckevisa funktioner är det viktigt att se till att varje formel tillämpas på sin rätta domän. \text{ if }{ 0 }<{ g }<{ 2 }\\\10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

I det här fallet är utgången 25 för varje ingång mellan 0 och 2. För värden som är lika med eller större än 2 definieras utgången som 10g+5.

Exempel

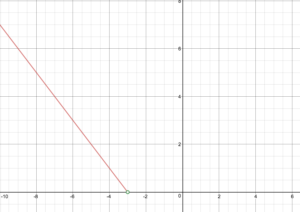
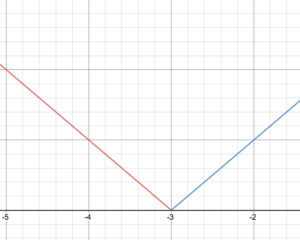
Skissa en graf för funktionen.

Med tanke på den styckevisa definitionen f(x)=\begin{cases}-x – 3\text{ if }x < -3\\ x + 3\text{ if }x < -3\ x + 3\text{ if } x \ge -3\end{cases}
Rita grafen för f.
Ange funktionens domän och intervall.

Visa svar

Grafera först linjen f(x) = -x-3 genom att radera den del där x är större än -3. Placera en öppen cirkel vid (-3,0).

Placera nu linjen f(x) = x+3 på grafen, med början vid punkten (-3,0). Observera att för denna del av grafen är punkten (-3,0) inkluderad, så du kan ta bort den öppna cirkeln.

De två graferna möts i punkten (-3,0)

Domänen för den här funktionen är alla reella tal eftersom (-3,0)inte är inkluderad som ändpunkt för f(x) = -x-3, men den är inkluderad som ändpunkt för f(x) = x+3.

Det här funktionsområdet börjar vid f(x)=0 och inkluderar 0, och går till oändligheten, så vi skulle skriva detta som x\ge0

I nästa exempel kommer vi att grafera en styckevis definierad funktion som modellerar fraktkostnaden för en serietidningsåterförsäljare på nätet.

Exempel

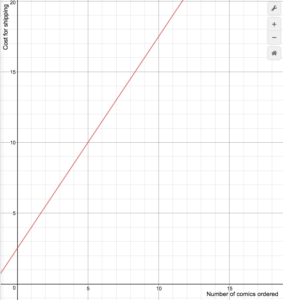
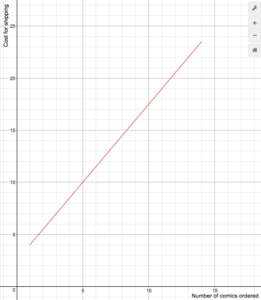
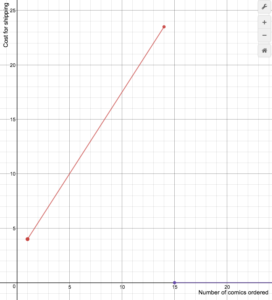
En återförsäljare av serietidningar på nätet tar ut fraktkostnader enligt följande formel

S(n)=\begin{cases}1,5n+2.5\text{ if }1\le{n}\le14\\\0\text{ if }n\ge15\end{cases}

Rita en graf över kostnadsfunktionen.

Visa svar

Tackla först upp linjen S(n)=1,5n+2,5. Vi kan använda oss av transformationer: detta är en vertikal sträckning av identiteten med en faktor 1,5 och en vertikal förskjutning med 2,5.

S(n)=1,5n+2.5

Nu kan vi eliminera de delar av grafen som inte ligger inom domänen baserat på 1\le{n}\le14

S(n) = 1,5n+2,5 för 1<=n<=14

Slutligt lägger vi till den konstanta funktionen S(n)=0 för ingångar som är större än eller lika med 15. Placera slutna prickar i slutet av grafen för att visa att slutpunkterna är inkluderade.

I följande video visar vi hur man graferar en styckevis definierad funktion som är linjär över båda domänerna.

Sammanfattning

• En styckevis definierad funktion är en funktion där mer än en formel används för att definiera utgången över olika delar av domänen
• Utvärdering av en styckevis definierad funktion innebär att du måste vara mycket uppmärksam på det korrekta uttrycket som används för den givna indata

För att grafera styckevis definierade funktioner identifierar du först var domänen är delad. Grafiska funktioner på domänen med hjälp av verktyg som t.ex. plottning av punkter eller transformationer. Var noga med att använda öppna eller slutna cirklar på ändpunkterna i varje domän beroende på om ändpunkten är inkluderad

.