Halvadder och full adderkrets
Halvadder och full adderkretsar förklaras med deras sanningstabeller i den här artikeln. Konstruktionen av en full adderare med hjälp av en halv adderarkrets visas också. Enbitarskretsen för full adderare och multibitsaddition med hjälp av full adderare visas också.
För att gå in på detta ämne är det mycket viktigt att känna till boolesk logik och logiska grindar.
Tillbaka till BOOLEAN LOGIC
Tillbaka till LOGIC GATES
Tillbaka till FLIP FLOPS
Vad är en adderare?
En adderare är en typ av kalkylator som används för att addera två binära tal. När jag säger miniräknare menar jag inte en med knappar, utan detta är en krets som kan integreras med många andra kretsar för ett brett spektrum av tillämpningar. Det finns två typer av adderare;
- Halvadderare
- Fulladderare
Halvadderare
Med hjälp av halvadderare kan vi konstruera kretsar som klarar av att utföra enkel addition med hjälp av logiska grindar.
Låt oss först ta en titt på addition av enskilda bitar.
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
Dessa är de minst möjliga kombinationer av enskilda bitar. Men resultatet för 1+1 är 10. Även om det här problemet kan lösas med hjälp av en EXOR-port, måste summaresultatet skrivas om som en 2-bitarsutgång om du bryr dig om utgången.
Därmed kan ovanstående ekvationer skrivas som
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
Här blir utgången ’1’av ’10’ carry-out. Resultatet visas i en sanningstabell nedan. ”SUM” är den normala utgången och ”CARRY” är utgången.
INPUTS OUTPUTS
A B SUM CARRY
0 0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
Från ekvationen, är det tydligt att denna 1-bitars adderare enkelt kan implementeras med hjälp av en EXOR-port för utgången ”SUM” och en AND-port för överföringen. Ta en titt på implementationen nedan.
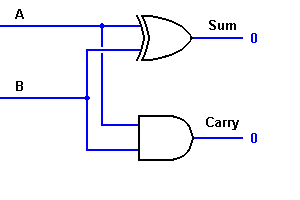
För komplexa additioner kan det finnas fall då man måste addera två 8-bitars bytes tillsammans. Detta kan endast göras med hjälp av fulladderlogik.
Fulladder
Denna typ av adderare är lite svårare att implementera än en halvadder. Den största skillnaden mellan en halvadder och en fulladder är att fulladdern har tre ingångar och två utgångar. De två första ingångarna är A och B och den tredje ingången är en inkommande carry som betecknas CIN. När en fullständig adderarlogik är konstruerad kommer vi att kunna kedja ihop åtta av dem för att skapa en adderare med bytebredd och kaskadera överföringsbiten från en adderare till nästa.
Utgångsöverföringen betecknas som COUT och den normala utgången betecknas som S. Ta en titt på sanningstabellen.
INPUTS OUTPUTS
A B CIN COUT S
0 0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 0 0 1
0 1 1 1 1 0
1 0 0 0 0 0 1
1 0 1 1 1 0
1 1 0 1 0
1 1 1 1 1 1
Från ovanstående sanning-tabellen, kan den fullständiga adderarlogiken implementeras. Vi kan se att utgången S är en EXOR mellan ingången A och halvadderutgången SUM med ingångarna B och CIN. Vi måste också notera att COUT bara blir sant om någon av de två ingångarna av de tre är HIGH.
Därmed kan vi implementera en fullständig adderkrets med hjälp av två halva adderkretsar. Den första halvadderaren kommer att användas för att addera A och B för att producera en partiell summa. Den andra halvadderlogiken kan användas för att lägga till CIN till den summa som produceras av den första halvadderaren för att få den slutliga S-utgången. Om någon av halvadderlogikerna producerar en överföring, kommer det att finnas en överföringsutgång. COUT blir således en OR-funktion av halvadderarnas Carry-utgångar. Ta en titt på genomförandet av den fullständiga adderarkretsen som visas nedan.
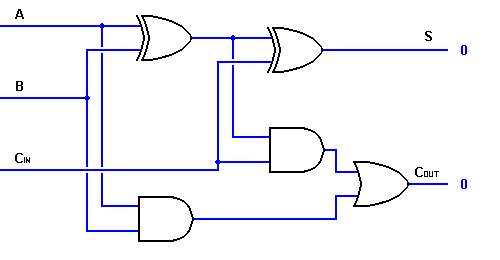
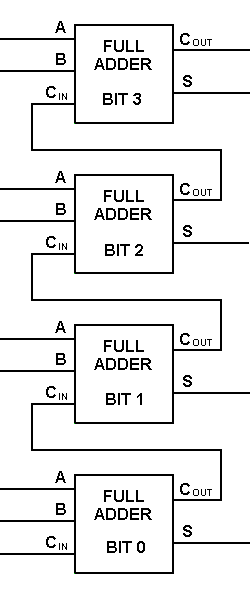
Tyvärr är det möjligt att genomföra större logikdiagram med ovanstående logik för fullständig adderare, men en enklare symbol används oftast för att representera operationen. Nedan ges en enklare schematisk representation av en enbits full adderare.
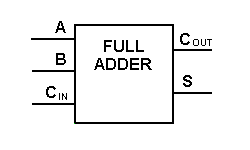
Med denna typ av symbol kan vi addera två bitar tillsammans och ta en carry från nästa lägre storleksordning och skicka en carry till nästa högre storleksordning. I en dator, för en operation med flera bitar, måste varje bit representeras av en full adderare och måste adderas samtidigt. För att addera två 8-bitarstal behöver man alltså 8 fullständiga adderare som kan bildas genom att kaskadera två av 4-bitsblocken. Additionen av två 4-bitarstal visas nedan.