Standardformeln för att hitta determinanten för en 3×3 matris är en uppdelning av mindre 2×2 determinantproblem som är mycket lätta att hantera. Om du behöver en uppfräschning kan du kolla in min andra lektion om hur man hittar determinanten till en 2×2-matris. Anta att vi får en kvadratisk matris A där,
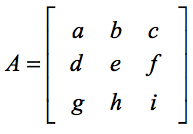
Matris A:s determinant beräknas som
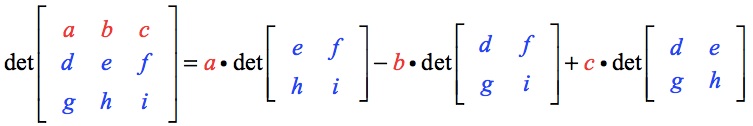
Här är de viktigaste punkterna:
- Bemärk att de översta radens element, nämligen a, b och c, tjänar som skalariska multiplikatorer till en motsvarande 2×2-matris.
- Skalaren a multipliceras till 2×2-matrisen av överblivna element som skapas när vertikala och horisontella linjesegment dras som passerar genom a.
- Samma process tillämpas för att konstruera 2×2-matriserna för skalära multiplikatorer b och c.
Determinanten till en 3×3-matris (animerad)

Exempel på hur man hittar determinanten till en 3×3-matris
Exempel 1: Hitta determinanten för 3×3-matrisen nedan.
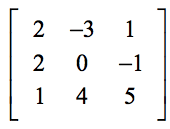
Uppställningen nedan hjälper dig att hitta överensstämmelsen mellan de generiska elementen i formeln och elementen i det faktiska problemet.
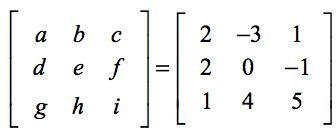
Om du tillämpar formeln,


Exempel 2: Utvärdera bestämningsfaktorn för 3×3-matrisen nedan.
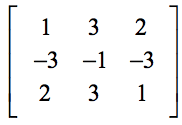
Var mycket försiktig när du sätter in värdena på rätt plats i formeln. Vanliga fel uppstår när eleverna blir slarviga under det första steget av substitutionen av värdena.
Ta dessutom tid på dig för att se till att din aritmetik också är korrekt. Annars kommer ett enda fel någonstans i beräkningen att ge ett felaktigt svar i slutändan.
Då,
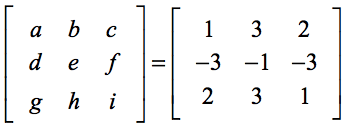
vår beräkning av determinanten blir…

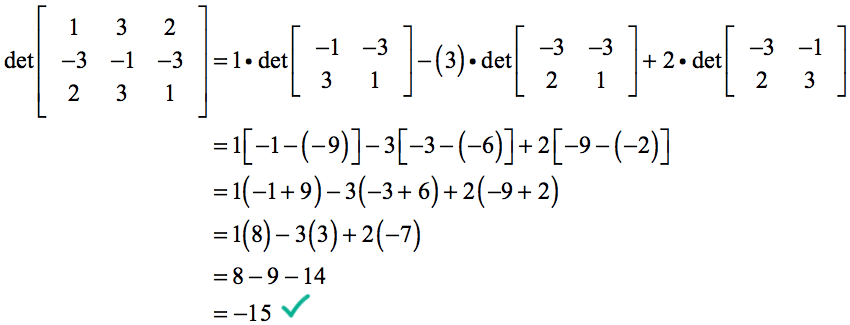
Exempel 3: Lös bestämningsfaktorn för determinanten för 3×3-matrisen nedan.
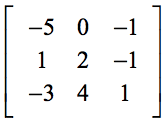
Närvaron av noll (0) i den första raden bör göra vår beräkning mycket enklare. Kom ihåg att dessa element i den första raden fungerar som skalära multiplikatorer. Därför kommer noll multiplicerat med något att leda till att hela uttrycket försvinner.