Fjärdeklassare Alice frågar: ”Hur många diagonaler är det i en decagon?”
Genial fråga, Alice. Men istället för att ge dig ett svar på den frågan ska jag visa dig hur du kan räkna ut det själv. Och inte bara det, jag ska visa dig hur du kan räkna ut svaret för vilken polygon som helst, även om den har 20, eller 50, eller 2000 sidor!
Är du redo? Vi börjar med ett enkelt exempel. Vi tar en polygon som har åtta sidor (vilket kallas en oktagon), så här:
Nu har den här polygonen, eftersom den har åtta sidor, också åtta hörn. Det verkar lite överväldigande att försöka räkna ut alla diagonaler, så låt oss bara fokusera på ett hörn. Hur många diagonaler kan du rita i en oktagon som alla börjar vid ett hörn?
Svaret på den frågan är fem. Ta en titt på diagrammet nedan:

I det här diagrammet har jag valt diagonalen till vänster precis under det översta hörnet, och jag har ritat diagonaler till varje hörn som jag kan rita en diagonal till. Vilka diagonaler kan jag inte rita diagonaler till? Jag kan inte rita en diagonal från en topp tillbaka till sig själv, och jag kan inte rita diagonaler till de två topparna bredvid denna topp (eftersom det inte skulle vara diagonaler utan sidor!).
Det finns alltså tre toppar som jag inte kan rita diagonaler till från denna topp. Åtta hörn totalt, minus de tre som jag inte kan rita till, återstår fem. Det är viktigt att komma ihåg: subtrahera 3 från antalet hörn, så har du antalet diagonaler som du kan dra från varje hörn.
Men det är bara ett hörn! Du skulle kunna rita diagonaler från vilken spets som helst, eller hur? Visst! Och det finns åtta hörn i vår oktagon, så vi tar antalet diagonaler per hörn och multiplicerar det med antalet hörn: 5 x 8 = 40.
Du kanske frestas att tro att det är vårt svar, men det är det inte. Varför inte? Därför att vi har räknat varje diagonal två gånger! Varje diagonal har två hörn, så vi har räknat den från den ena änden, och vi har också räknat den från den andra änden. Så för att få fram det faktiska antalet diagonaler måste vi dela vårt svar med 2. 40 / 2 = 20. Det finns tjugo diagonaler i en oktagon.
Låt oss prova detta resonemang på en polygon som har 2000 sidor. Nu tänker jag inte rita en 2000-gon för er; vi måste bara räkna ut resonemanget utan en bild.
- Välj en hörnpunkt. Hur många diagonaler kan du rita från detta hörn? Svar: 2000 – 3 = 1997.
- Hur många hörn totalt? Svar: 2000
- Hur många diagonaler räknat från alla hörn? Svar: 1997 x 2000 = 3 994 000
- Oj! Vi har räknat varje diagonal två gånger! Hur gör vi oss av med dubbelräkningen? Svar: Vi tar bort de dubbla diagonalerna: 3994000 / 2 = 1 997 000
En 2000-gon har alltså 1 997 000 diagonaler!
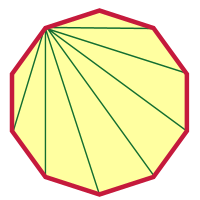
Efter att ha gjort något så galet som en 2000-gon borde en decagon inte verka så svår, eller hur? Jag ska få dig att börja, och du kan avsluta det härifrån. Jag valde ett hörn och ritade diagonaler från det hörnet.
Hur många är det? Kunde du räkna ut hur många det var utan att titta på bilden?
Kan du räkna ut det härifrån? Jag hoppas det! Lycka till, Alice.
Förresten finns det en formel som du kan använda; den ser ut så här: D = n(n – 3)/2. Men ärligt talat förväntar jag mig inte att mina elever ska memorera den. Jag förväntar mig att de ska komma ihåg hur vi resonerar här. Om man förstår logiken är det till och med bättre än att ha en formel!