GENERAL CHEMISTRY TOPICS
Energi: Grundläggande begrepp
Energiformer: Kinetisk och potentiell energi.Arbete och energi.Värme och temperatur.Elektrostatisk potentiell energi.
Energi: kinetisk och potentiell energi
Begreppet energi är grundläggande för de fysikaliska vetenskaperna. Här vill vi fastställa några första principer om energi och presentera några av de former som energi antar och som är av särskild betydelse för kemin. Först och främst är det ofta mycket användbart att definiera ett system som en särskild del av universum på vilken våra observationer görs. Systemet består av ett objekt eller en samling objekt och skiljer sig från resten av universum – som vi kallar omgivningen – genom en verklig eller imaginär gräns.
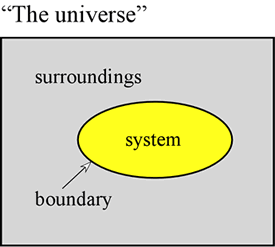
Ett gasprov som hålls inom en fast volym, t.ex. en metallcylinder, är ett exempel på ett system – ett system som kommer att vara av betydelse för oss när vi tar oss an studiet av gasers allmänna egenskaper. Ytterligare exempel är ett gasprov inuti en ballong eller en förbränningsblandning i en cylinder med en kolv. I båda dessa fall är systemet omslutet av en fysisk, men rörlig gräns, så att systemets volym inte är fast. Ytterligare ett exempel som vi ofta kommer att beakta är en blandning av ämnen i lösning som genomgår en kemisk reaktion i ett provrör eller en bägare. Den terminologi som introduceras här är av särskild betydelse för studiet av hur energi manifesteras i kemiska system, vilket till stor del faller under rubriken termodynamik.
I den allmänna kemin är de system som vi betraktar som relevanta vanligtvis i vila och gravitationseffekter ignoreras. Ofta är vi mest intresserade av system inom vilka kemiska reaktioner äger rum, där systemets kemiska sammansättning förändras med tiden. Låt oss dock för tillfället anta ett bredare perspektiv genom att använda mekaniska system som en svängande pendel eller biljardkulor som rullar och kolliderar, för att hjälpa oss att förstå allmänna principer som rör energi.
Ett system kan sägas besitta energi på två olika sätt, som vi kallar kinetisk och potentiell energi. Kinetisk energi är energin hos materia i rörelse. Fysiken ger en exakt matematisk definition av kinetisk energi (KE), som visas i ekvationen (nedan till vänster).
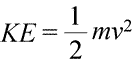
Här representeras ett föremåls kinetiska energi som en produkt av föremålets massa (m) och kvadraten på dess hastighet (v), multiplicerad också med konstanten ½. Om systemet består av mer än ett objekt kan den totala kinetiska energin uttryckas som en summa av de enskilda objektens kinetiska energier.
Vi kan härleda enheter för energi givet denna definition. SI-enheten för energi är joule (J), som definieras som:
1 J = 1 kg-m-s-2
Potentialenergi är energin i ett system som typiskt sett kan omvandlas till rörelseenergi i någon form, och som kan producera, i något mått, en kvantitet som kallas arbete (diskuteras vidare nedan). Ett tydligt exempel på potentiell energi är en tegelsten på kanten av en byggnad. Tegelstenen har en viss mängd potentiell energi på grund av sin höjd – dess placering i förhållande till ett gravitationsfält. Om vi ger tegelstenen en knuff, så att den faller ner från kanten, rör den sig spontant i riktning mot lägre potentiell gravitationsenergi, och när den gör det får den kinetisk energi. Ett annat exempel är den elektriska potentiella energin i ett batteri (som uttrycks i termer av spänning). När en krets skapas med en tråd och en glödlampa, som förbinder batteriets två terminaler, orsakar skillnaden i elektrisk potential mellan dem att elektronerna i tråden rör sig (kinetisk energi), vilket resulterar i produktion av både värme och ljus.
En viktig allmän princip om energi är att den varken kan skapas eller förstöras. Detta är känt som lagen om energins bevarande. Kvantitativt sett innebär detta att i ett system som den fallande tegelstenen eller klockans pendel är summan av kinetisk och potentiell energi konstant. Detta är något av en abstraktion, eftersom en del av energin i en riktig pendel ständigt går förlorad på grund av friktion, och en liten mängd energi måste tillföras pendeln för att den ska fortsätta att svänga (och klockan fungera). Men om vi tar hänsyn till denna ”förlorade” energi (som i själva verket uppträder som en ökning av värmeenergin hos de omgivande luftmolekylerna) genom noggranna experimentella mätningar, visar det sig att energin faktiskt alltid bevaras. Ett annat förbehåll sammanfattas i Einsteins berömda ekvation E = mc2, som uttrycker en grundläggande ekvivalens mellan massa och energi. En mer allmän form av lagen om energins bevarande, som kan kallas lagen om massans och energins bevarande, tar hänsyn till denna ekvivalens. Om vi återvänder till den allmänna kemin så är sådana omvandlingar mellan materia och energi inte typiskt sett dess område, medan studiet av kärnreaktioner och radioaktivitet omfattas av kärnfysiken.
Om vi betraktar en kemisk reaktion där de kemiska förändringarna åtföljs av värmeproduktion, uppstår en fråga: Hur är det med bevarandet av energin i detta fall? Svaret är att det finns en form av potentiell energi, som vi kan kalla kemisk potentiell energi (eller helt enkelt kemisk potential), som kan tänkas finnas i reaktanternas molekylära sammansättning. Denna potentiella energi omvandlas sedan till energi i form av värme, men det visar sig att nettomängden närvarande energi förblir konstant när vi väl kan definiera och mäta värmeproduktionen. Ett vardagligt exempel på vad vi nu kan förstå som kemisk potentiell energi ges av en bensinmotor, där blandningen av bensin och syre besitter en latent form av energi. Denna latenta energi i blandningen av bensin och syre förbrukas för att producera den kinetiska energin i en bil.
Arbete och energi
Arbete är ett annat begrepp som medger en exakt definition inom fysiken. Dessutom kan mekanikens lagar knytas till energi med hjälp av teoremet arbete-energi. En spark av en fotboll, eller ett antal liknande exempel, illustrerar idén att ett föremåls rörelseenergi kan ökas genom att man utövar en kraft. Arbete-energi-satsen, som är en generalisering av denna idé, kan i grova drag formuleras på följande sätt: Förändringen av den energi som ett föremål har är lika med storleken på den kraft som verkar på det, multiplicerat med det avstånd genom vilket kraften verkar.
Den energiförändring som sker i ett system till följd av arbete kan vara positiv eller negativ, ur systemets synvinkel. Arbete kan utföras av ett system, eller så kan ett system få arbete utfört på sig av omgivningen. Om arbete utförs av ett system förlorar det energi till omgivningen. Om systemet får arbete utfört på sig ökar systemets energi. När t.ex. en gnista som startar en förbränningsblandning i en cylinder med en rörlig kolv orsakar en snabb expansion av systemet, och expansionen är mekaniskt kopplad till rörelsen av en stång i omgivningen, utför cylinderns system arbete på omgivningen och förlorar på så sätt energi. Detta är naturligtvis en del av hur en förbränningsmotor omvandlar kemisk potentiell energi till den kinetiska energin hos en bil i rörelse.
En implikation av teoremet arbete-energi gäller enheter, nämligen att arbete kan mätas i samma enheter som energi. Eftersom Newtons andra lag är kraft = massa × acceleration, härleds newton (N), SI-enheten för kraft, till M × L × T -2, och därmed är 1 N = 1 kg m s-2. Kraft gånger avstånd har kvantiteterna M × L2 × T -2, och därför definieras SI-enheten för energi, joule (J), som 1 J = 1 kg m2 s-2. Vid det här laget bör du själv kontrollera att ekvationen för kinetisk energi innefattar samma kombination av de grundläggande storheterna massa (M), längd (eller avstånd, L) och tid (T).
Värme och temperatur
Vi använder orden värme och temperatur ganska ofta och talar ofta om värme som en form av energi. Vi har alla en intuitiv känsla för vad dessa saker är, men här vill vi tänka mer vetenskapligt på dem och ge dem mer formella definitioner om vi kan. Detta är en nödvändig förberedelse för att kvantifiera den energi som motsvarar värme, och därmed för att göra mätningar för att kontrollera lagen om energins bevarande. Vad vi finner är att värmeenergin i ett system kan liknas vid den totala rörelseenergin (enligt definitionen ovan) hos de atomer och molekyler som ingår i systemet. Ett föremåls eller systems temperatur är i själva verket ett mått på den genomsnittliga rörelseenergin hos de ingående atomerna och/eller molekylerna. (Observera att temperaturen inte är exakt lika med den genomsnittliga molekylära kinetiska energin, men är direkt proportionell mot den. Mer information finns på webbsidan om kinetisk molekylteori).
Ett sätt att visualisera vad vi menar med värme och temperatur, och skillnaden mellan dem, är att betrakta en biljardbollsanalogi. I vissa enkla sammanhang är beteendet hos biljardkulor en lämplig modell för en samling atomer eller molekyler, t.ex. i ett gasprov. Precis som biljardkulor som just har träffats av en snabbt rörlig köboll rör sig gasmolekylerna runt och studsar mot varandra och mot väggarna i den behållare som innehåller dem. Biljardbollarnas totala kinetiska energi, som bara är summan av varje bolls individuella kinetiska energi, motsvarar den termiska energin i ett prov av gasmolekyler. Vid en ”paus” i början av ett biljardspel fördelas köbollens ursprungliga rörelseenergi mellan alla bollar på bordet. Vissa rör sig ganska snabbt och andra inte lika snabbt, men analogin till ”värme” eller ”termisk energi” för systemet med biljardkulor är bara summan av dessa kinetiska energier. Å andra sidan skulle temperaturen i systemet med biljardkulor vara proportionell mot den genomsnittliga rörelseenergin i ensemblen av kulor.
Elektrostatisk potentiell energi
Lagen om elektrostatisk attraktion och repulsion, eller Coulombs lag, beskriver den kraft som utövas på ett laddat objekt på grund av närvaron av ett annat laddat objekt. Kraften är lättast att beräkna när laddningarna kan behandlas som mycket små punktladdningar. Storleken på den kraft som ett laddat föremål ”känner” är proportionell mot produkten av laddningarna (SI-enheten för elektrisk laddning är Coulomb, C) och omvänt proportionell mot kvadraten på avståndet mellan laddningarna (r i figuren till höger). Kraften är en attraherande kraft (som gravitation, och indikeras av inåtriktade pilspetsar i figuren) om laddningarna har motsatt tecken, och avstötande när laddningarna har samma tecken.
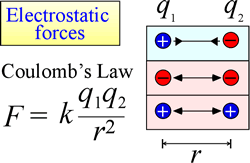
När krafter (t.ex. elektrostatiska, magnetiska och gravitationella krafter) kan verka på distans (genom rymden, utan mekanisk kontakt) sägs föremålen som är utsatta för sådana krafter befinna sig i ett potentiellt energifält. Vi talade om gravitationell potentiell energi ovan, och på samma sätt när det gäller elektrostatiska krafter kommer ett laddat föremål att ha elektrostatisk potentiell energi på grund av att det befinner sig i ett elektriskt fält. Ett sådant fält finns i närheten av alla andra laddningar.
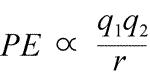
Ekvation för elektrostatisk potentiell energi: Den potentiella energins form följer matematiskt av kraftuttrycket Coulombs lag.
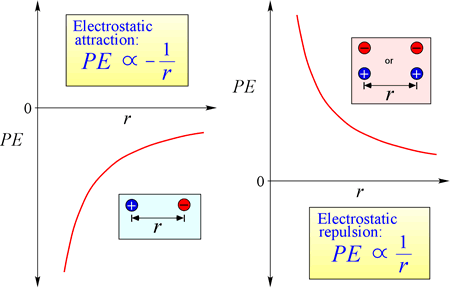
Genom de motsatta tecknen på de laddningar som attraheras är den potentiella energin alltid negativ, och ju närmare laddningarna närmar sig varandra, desto mer negativ – dvs. desto lägre – blir den potentiella energin. När separationsavståndet r närmar sig noll blir den potentiella energin oändligt negativ. För laddningar med samma tecken är den potentiella energin för avstötning alltid positiv och blir oändligt positiv när separationsavståndet r närmar sig noll.
Elektrostatisk potentiell energi är en viktig faktor inom kemin. En förståelse av atomens natur, kemisk bindning och intermolekylära krafter är alla absolut beroende av att redovisa inflytandet av laddning- laddningsinteraktioner som bidrar till energin i ett system.
Viktiga enheter
Energi (SI-enhet) 1 joule = 1 J = 1 kg-m-s-2
Elementarladdning, e = 1,60218 × 10-19 C (coulomb, C)
Faradaykonstant: F = NAe = 9,64853 × 104 C-mol-1
Elektrisk potential: volt, V 1 V = 1 J C-1