Det är inte ofta som en matematisk ekvation hamnar i den nationella pressen, än mindre i den populära radion, eller, vilket är mest häpnadsväckande av allt, är föremål för en debatt i det brittiska parlamentet. År 2003 var dock den goda gamla kvadratiska ekvationen, som vi alla lärde oss om i skolan, allt detta.
Vad vi börjar

Det hela började vid ett möte med National Union of Teachers. Den kvadratiska ekvationen hölls högt för nationen som ett exempel på den grymma tortyr som matematikerna tillfogade stackars intet ont anande skolbarn. Den kvadratiska ekvationen, som var fascinerad av denna anklagelse, fick en huvudroll i radio på bästa sändningstid, där den ifrågasattes av en formidabel intervjuare som var mer van vid att ta sig an premiärministern. Times (London) tog plats i sin ledarkrönika, som vanligtvis är reserverad för tunga diskussioner om den moderna världens moraliska hälsa (eller inte), för att förkunna att den kvadratiska ekvationen var värdelös, att matematik var värdelös och att ingen ville studera matematik i alla fall, så varför bry sig om det? Eftersom man var orolig för att de farliga antagandena från den kvadratiska ekvationen skulle förbli oemotsagda debatterades ekvationens avgörande betydelse för Förenade kungarikets överlevnad (en positiv ståndpunkt intogs, vilket kanske gläder er att få veta) i det brittiska underhuset.
Var skulle allt sluta? Var den kvadratiska ekvationen verkligen död? Var det någon som brydde sig? Är matematiker verkligen onda monster som bara vill åsamka en yngre generation kvadratiska ekvationer som ett sätt att korrumpera deras odödliga själar?
Kanske det, men det är egentligen inte den kvadratiska ekvationens fel. Faktum är att den kvadratiska ekvationen har spelat en central roll inte bara för hela den mänskliga civilisationen som vi känner den, utan även för den möjliga upptäckten av andra utomjordiska civilisationer och till och med för sådana vitala moderna aktiviteter som att titta på satellit-tv. Vad mer, bortsett från den gudomliga uppenbarelsens natur, kan anses ha haft en sådan inverkan på livet som vi känner det? På ett mycket konkret sätt kan kvadratiska ekvationer faktiskt rädda ditt liv.
Babylonierna
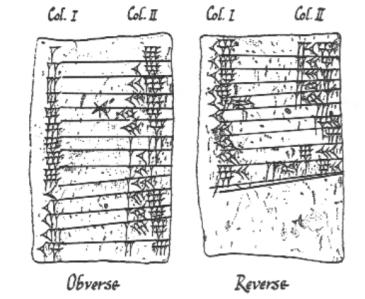
Babyloniska kilskriftstavlor som registrerar de nio tidtabellerna
Allt började omkring 3000 f.Kr. med babylonierna. De var en av världens första civilisationer och kom med några fantastiska idéer som jordbruk, bevattning och skrivning. De ritade solens, månens och planeternas banor och antecknade dem på lertavlor (som du fortfarande kan se på British Museum). Till babylonierna har vi att tacka för de moderna idéerna om vinklar, inklusive det sätt på vilket cirkeln delas upp i 360 grader (på grund av ett litet räknefel, en per dag). Vi har också babylonierna att tacka för den mindre trevliga uppfinningen av den (fruktade) skattemannen. Och detta var en av anledningarna till att babylonierna behövde lösa kvadratiska ekvationer.
Vi antar att du är en babylonisk jordbrukare. Någonstans på din gård har du ett kvadratiskt fält på vilket du odlar någon gröda. Hur mycket av din gröda kan du odla på fältet? Om du fördubblar längden på varje sida av fältet finner du att du kan odla fyra gånger så mycket av grödan som tidigare. Anledningen till detta är att den mängd gröda som du kan odla är proportionell mot fältets yta, som i sin tur är proportionell mot kvadraten på sidans längd. I matematiska termer, om  är längden på sidan av fältet, är
är längden på sidan av fältet, är 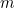 den mängd gröda du kan odla på ett kvadratiskt fält med sidlängden 1, och
den mängd gröda du kan odla på ett kvadratiskt fält med sidlängden 1, och  är den mängd gröda som du kan odla, då
är den mängd gröda som du kan odla, då
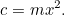 |
Detta är vår första kvadratiska ekvation, naken och blinkande i solljuset. Kvadratiska ekvationer och areor är kopplade till varandra som bröder och systrar i samma familj. Just nu behöver vi dock inte lösa något – tills skattemannen kommer, vill säga! Glatt säger han till bonden ”Jag vill att du ger mig grödor för att betala skatterna på din gård”. Bonden står nu inför ett dilemma: Hur stor åker behöver han för att odla den mängden grödor? Vi kan enkelt besvara denna fråga, i själva verket
grödor för att betala skatterna på din gård”. Bonden står nu inför ett dilemma: Hur stor åker behöver han för att odla den mängden grödor? Vi kan enkelt besvara denna fråga, i själva verket
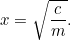 |
Finnandet av kvadratrötter med hjälp av en miniräknare är enkelt för oss, men var mer av ett problem för babylonierna. Faktum är att de utvecklade en metod för successiv approximation av svaret som är identisk med den algoritm (kallad Newton-Raphson-metoden) som används av moderna datorer för att lösa mycket svårare problem än kvadratiska ekvationer.
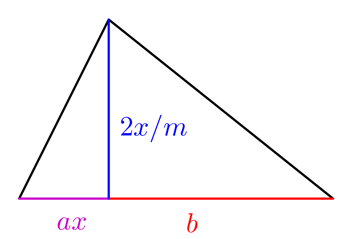
Nu är inte alla fält kvadratiska. Låt oss nu anta att jordbrukaren har ett mer udda fält med två triangulära sektioner som visas till höger.
För lämpliga värden på  och
och 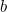 ges mängden gröda som bonden kan odla på detta fält av
ges mängden gröda som bonden kan odla på detta fält av
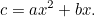 |
Detta liknar mycket mer den kvadratiska ekvation som vi är vana vid, och även under skattemännens onda öga är den mycket svårare att lösa. Ändå kom babylonierna på svaret igen. Först dividerar vi med  för att få
för att få
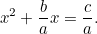 |
Nu kompletterar vi kvadraten genom att använda det faktum att
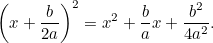 |
Genom att kombinera detta med den ursprungliga ekvationen får vi
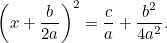 |
Detta är nu en ekvation som vi kan lösa genom att ta kvadratrötter. Resultatet är den berömda ”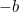 -formeln”:
-formeln”:
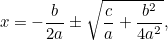 |
som kan skrivas om som
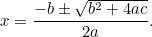 |
(Formeln har vanligtvis ”-4ac” eftersom den kvadratiska ekvationen oftast skrivs i formen ”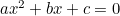 ”.)
”.)
Det faktum att det kan ge ett positivt eller negativt svar att ta en kvadratrot leder till det anmärkningsvärda resultatet att en kvadratisk ekvation har två lösningar. Så mycket för att matematiska pussel bara har en lösning!
Nu är det här som undervisningen om kvadratiska ekvationer ofta stannar upp. Vi har nått fram till det objekt som alla journalister älskar när de intervjuar matematiker – en formel. Det går att hitta på oändliga frågor som går ut på att sätta in värden av 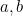 och
och  i formeln för att få fram (två) svar. Men detta är inte alls vad matematik handlar om. Att hitta en formel är bara det första steget på en lång väg. Vi måste fråga oss vad formeln betyder, vad säger den oss om universum, spelar det verkligen någon roll att ha en formel? Låt oss nu se vart denna formel tar oss.
i formeln för att få fram (två) svar. Men detta är inte alls vad matematik handlar om. Att hitta en formel är bara det första steget på en lång väg. Vi måste fråga oss vad formeln betyder, vad säger den oss om universum, spelar det verkligen någon roll att ha en formel? Låt oss nu se vart denna formel tar oss.
En överraskning för grekerna, lite matematisk origami och känsla för proportioner
Vi spolar nu 1000 år framåt till de gamla grekerna och ser vad de gjorde av kvadratiska ekvationer. Grekerna var suveräna matematiker och upptäckte mycket av den matematik som vi fortfarande använder idag. En av de ekvationer de var intresserade av att lösa var den (enkla) kvadratiska ekvationen
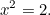 |

De visste att denna ekvation hade en lösning. I själva verket är det längden på hypotenusan i en rätvinklig triangel som hade sidor av längden ett.
Det följer av Pythagoras’ sats att om en rätvinklig triangel har en vinkelrätt triangel, så är det en triangel som har en vinkelrätt triangel som har en vinkelrätt triangel.vinklad triangel har kortare sidor  och
och  och hypotenusan
och hypotenusan  så
så
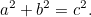 |
Om man sätter 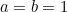 och
och  så
så 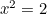 . Således
. Således 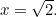
Så, vad är  i detta fall? Eller, för att ställa den fråga som grekerna ställde, vilket slags tal är det? Anledningen till att detta hade betydelse låg i grekernas känsla för proportioner. De trodde att alla tal stod i proportion till varandra. För att vara exakt innebar detta att alla tal var bråk av formen
i detta fall? Eller, för att ställa den fråga som grekerna ställde, vilket slags tal är det? Anledningen till att detta hade betydelse låg i grekernas känsla för proportioner. De trodde att alla tal stod i proportion till varandra. För att vara exakt innebar detta att alla tal var bråk av formen 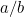 där
där  och
och  är hela tal. Tal som 1/2, 3/4 och 355/113 är alla exempel på bråk. Det var naturligt att förvänta sig att
är hela tal. Tal som 1/2, 3/4 och 355/113 är alla exempel på bråk. Det var naturligt att förvänta sig att  också var ett bråk. Den stora överraskningen var att det inte är det. I själva verket
också var ett bråk. Den stora överraskningen var att det inte är det. I själva verket
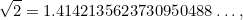 |
där prickarna  betyder att decimalutvidgningen av
betyder att decimalutvidgningen av  fortsätter i oändlighet utan något urskiljbart mönster. (Vi kommer att möta denna situation igen senare när vi lär oss om kaos.)
fortsätter i oändlighet utan något urskiljbart mönster. (Vi kommer att möta denna situation igen senare när vi lär oss om kaos.)
 var det första irrationella talet (det vill säga ett tal som inte är en bråkdel, eller rationellt), som erkändes som sådant. Andra exempel är
var det första irrationella talet (det vill säga ett tal som inte är en bråkdel, eller rationellt), som erkändes som sådant. Andra exempel är 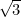 ,
,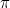 ,
,  och i själva verket ”de flesta” tal. Det dröjde ända till 1800-talet innan vi hade ett bra sätt att tänka på dessa tal. Upptäckten att
och i själva verket ”de flesta” tal. Det dröjde ända till 1800-talet innan vi hade ett bra sätt att tänka på dessa tal. Upptäckten att  inte var ett rationellt tal orsakade både stor uppståndelse (100 oxar offrades till följd av detta) och stor chock, och upptäckaren tvingades begå självmord. (Låt detta vara en fruktansvärd varning för de matematiskt intresserade!) Vid denna tidpunkt gav grekerna upp algebra och övergick till geometri.
inte var ett rationellt tal orsakade både stor uppståndelse (100 oxar offrades till följd av detta) och stor chock, och upptäckaren tvingades begå självmord. (Låt detta vara en fruktansvärd varning för de matematiskt intresserade!) Vid denna tidpunkt gav grekerna upp algebra och övergick till geometri.
Långt ifrån att vara ett obskyrt tal möter vi  regelbundet: varje gång vi använder ett A4-papper. I Europa mäts pappersstorlekarna i A-storlekar, där A0 är det största med en yta på
regelbundet: varje gång vi använder ett A4-papper. I Europa mäts pappersstorlekarna i A-storlekar, där A0 är det största med en yta på 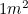 . A-storlekarna har ett särskilt förhållande till varandra. Om vi nu gör lite origami och tar ett ark A1-papper och viker det på mitten (längs den längsta sidan) får vi A2-papper. Om man viker det på mitten igen får man A3, och återigen får man A4 osv. Pappret är dock utformat så att proportionerna för varje A-storlek är desamma – det vill säga att varje pappersbit har samma form.
. A-storlekarna har ett särskilt förhållande till varandra. Om vi nu gör lite origami och tar ett ark A1-papper och viker det på mitten (längs den längsta sidan) får vi A2-papper. Om man viker det på mitten igen får man A3, och återigen får man A4 osv. Pappret är dock utformat så att proportionerna för varje A-storlek är desamma – det vill säga att varje pappersbit har samma form.
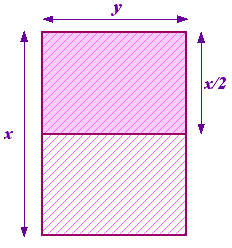
Vi kan ställa oss frågan om vilken proportion detta är. Börja med ett papper med sidorna x och y där x är den längsta sidan. Dela nu detta i två för att få ett annat pappersstycke med sidorna y och x/2 där nu y är den längsta sidan. Detta illustreras till höger.
Proportionerna för den första pappersbiten är 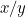 och proportionerna för den andra är
och proportionerna för den andra är 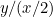 eller
eller 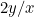 . Vi vill att dessa två proportioner ska vara lika stora. Detta innebär att
. Vi vill att dessa två proportioner ska vara lika stora. Detta innebär att
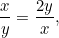 |
eller
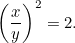 |
Ytterligare en kvadratisk ekvation! Som tur är är det en som vi redan har mött. Genom att lösa den finner vi att
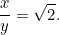 |
Detta resultat är lätt för dig att kontrollera. Ta ett A4-ark (eller A3- eller A5-ark) och mät sidorna. Vi kan också räkna ut storleken på varje ark. Arean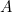 av ett papper A0 ges av
av ett papper A0 ges av
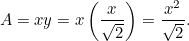 |
Men vi vet att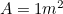 så vi har en annan kvadratisk ekvation för den längsta sidan
så vi har en annan kvadratisk ekvation för den längsta sidan av A0, som ges av
av A0, som ges av
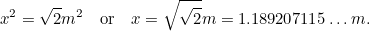 |
Detta betyder att den längsta sidan av A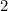 ges av
ges av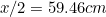 (varför?) och den till A
(varför?) och den till A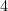 av
av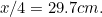 . Kontrollera detta på dina egna pappersark.
. Kontrollera detta på dina egna pappersark.
Papper som används i USA, som kallas foolscap, har en annan proportion. För att se varför återvänder vi till grekerna och en annan kvadratisk ekvation. Efter att ha orsakat sådan sorg, löser den kvadratiska ekvationen sig själv i sökandet efter de perfekta proportionerna: ett sökande som fortsätter idag i utformningen av filmkulisser, och som kan ses i många aspekter av naturen.
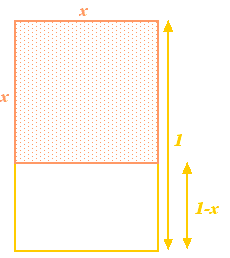
Låt oss börja med en rektangel, och sedan ta bort en kvadrat från den med samma sidlängd som den kortaste sidan i rektangeln. Om rektangelns längsta sida har längden 1 och den kortaste sidan har längden  , så har kvadraten sidor med längden
, så har kvadraten sidor med längden  . Om man tar bort den från rektangeln får man en mindre rektangel med längsta sidan
. Om man tar bort den från rektangeln får man en mindre rektangel med längsta sidan  och minsta sidan
och minsta sidan 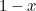 . Så långt, så abstrakt. Grekerna ansåg dock att den rektangel som hade de mest estetiska proportionerna (den så kallade gyllene rektangeln) var den för vilken den stora och den lilla rektangeln som konstruerats ovan har samma proportioner. För att detta ska vara möjligt måste vi ha
. Så långt, så abstrakt. Grekerna ansåg dock att den rektangel som hade de mest estetiska proportionerna (den så kallade gyllene rektangeln) var den för vilken den stora och den lilla rektangeln som konstruerats ovan har samma proportioner. För att detta ska vara möjligt måste vi ha
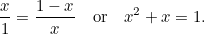 |
Detta är ännu en kvadratisk ekvation: en mycket viktig ekvation som dyker upp i alla möjliga tillämpningar. Den har den (positiva) lösningen
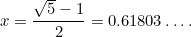 |
Talet  kallas det gyllene snittet och betecknas ofta med den grekiska bokstaven
kallas det gyllene snittet och betecknas ofta med den grekiska bokstaven 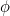 .
.

Den gyllene rektangeln kan ses i formen på fönster, särskilt på georgianska hus. På senare tid kan det gyllene snittet också hittas som den ”perfekta formen” för fotografier och filmbilder. Den kvadratiska ekvationen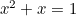 förekommer också i studier av kaninpopulationer och i det mönster i vilket solrosfröna och bladen på växternas stjälkar är arrangerade. Dessa är alla kopplade till det gyllene snittet genom Fibonacci-sekvensen som ges av
förekommer också i studier av kaninpopulationer och i det mönster i vilket solrosfröna och bladen på växternas stjälkar är arrangerade. Dessa är alla kopplade till det gyllene snittet genom Fibonacci-sekvensen som ges av
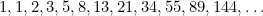 |

Solrosfrön, arrangerade med hjälp av Fibonacci-tal |
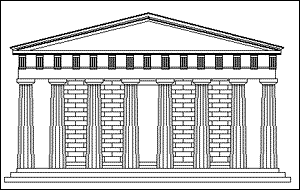
Parthenon, som förkroppsligar det gyllene snittet |
I denna sekvens är varje term summan av de två föregående termerna. Fibonacci upptäckte den på 1400-talet i ett försök att förutsäga den framtida kaninpopulationen. Om man tar förhållandet mellan varje term och den efterföljande får man talföljden
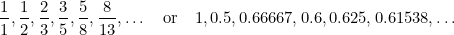 |
och dessa tal närmar sig alltmer (du gissade det) det gyllene snittet 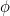 .
.
Genom att hitta båda rötterna till ovanstående kvadratiska ekvation kan vi faktiskt hitta en formel för den nionde termen i Fibonacci-sekvensen. Om  är det
är det 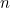 te sådana tal med
te sådana tal med 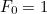 och
och 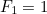 så ges
så ges  av formeln
av formeln
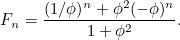 |
Konikerna kopplar kvadratiska ekvationer till stjärnorna

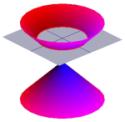
Grekerna var också mycket intresserade av konernas form. Bilden till vänster visar en typisk kon.
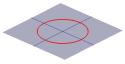
Hälften av konen kan visualiseras som spridningen av ljuset som kommer från en fackla. Om du nu lyser med en ficklampa på en plan yta, t.ex. en vägg, kommer du att se olika former när du förflyttar ficklampan. Dessa former kallas koniska sektioner och är de kurvor som man får om man tar ett snitt genom en kon i olika vinklar. Just dessa kurvor studerades av grekerna, och de insåg att det i princip fanns fyra typer av koniska snitt. Om man tar ett horisontellt snitt genom konen får man en cirkel. Ett snitt i en liten vinkel mot horisontalplanet ger en ellips. Om man tar ett vertikalt snitt får man en hyperbel och om man tar ett snitt parallellt med konens ena sida får man en parabel. Dessa kurvor illustreras nedan.
 |
 |
 |
 |
 |
 |
 |
 |

En korsningsnitt av en kon kan vara en cirkel … |

… en ellips … |
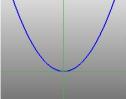
… en parabel … |
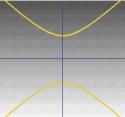
…. eller en hyperbel. |
Koniska sektioner kommer in i vår berättelse eftersom var och en av dem beskrivs av en kvadratisk ekvation. Särskilt om 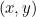 representerar en punkt på varje kurva, så kopplar en kvadratisk ekvation samman
representerar en punkt på varje kurva, så kopplar en kvadratisk ekvation samman  och
och 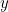 . Vi har:
. Vi har:
Cirkeln: 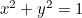 ;
;
Ellipsen: 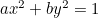 ;
;
Hyperbola: 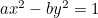 ;
;
Parabeln: 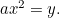
Dessa kurvor var kända och studerade sedan grekerna, men bortsett från cirkeln verkade de inte ha någon praktisk tillämpning. Som vi kommer att se i nästa nummer av Plus ledde dock en koppling mellan kvadratiska ekvationer och koniska kurvor, tillsammans med en mäktig lyckoträff, till en förståelse för hur universum fungerar, och på 1500-talet var det dags för koniska kurvor att förändra världen.
Om författarna
Chris Budd är professor i tillämpad matematik vid institutionen för matematiska vetenskaper vid University of Bath och ordförande i matematik vid Royal Institution i London.
Chris Sangwin är anställd vid School of Mathematics and Statistics vid University of Birmingham. Han är forskare vid Learning and Teaching Support Network centre for Mathematics, Statistics and Operational Research.
De har nyligen skrivit den populära matematikboken Mathematics Galore! som ges ut av Oxford University Press.
Denna artikel inspirerades delvis av en anmärkningsvärd debatt i det brittiska underhuset om kvadratiska ekvationer. Debatten finns i Hansard, United Kingdom House of Commons, 26 juni 2003, Columns 1259-1269, 2003, som finns tillgänglig online på House of Commons Hansard Debate website.